Acquisition en mode vidéo et traitement

Leçon 26 : Acquisition en mode vidéo et traitement

On décrit ci-après brièvement une variante des techniques scan qui permet d'acquérir des images planétaires à haute cadences tout en ne nécessitant pas l'usage d'un obturateur. C'est le mode de lecture vidéo du CCD. Cliquer ici pour avoir d'autres détails.

Sans obturateur et lorsqu'on vise un objet brillant, ici la planète Saturne, voici ce que l'on obtient :

Le phénomène de smearing rend l'image totalement inexploitable. Ce qu'il se passe : lors de la lecture du CCD, qui dure plusieurs secondes, la planète illumine toujours le détecteur et produit une trace parasite très intense au fur et à mesure que les charges sont transférées en colonne. La technique qui nous a permis de faire de la photométrie rapide au début de cette page se retourne à présent contre nous en nous empêchant d'observer les détails de la surface planétaire.

Dans le mode vidéo on produit un décalage particulier des charges électriques qui a pour effet de simuler la présence d'un obturateur. L'image est lue par groupes de 3 bandes. La séquence est la suivante : (1) lecture rapide de l'image électronique sur N lignes (l'information n'est même pas numérisée), (2) réalisation d'un délai d'attente qui est le temps de pose effectif et qui peu ne durer que quelques millisecondes, (3) lecture rapide des N lignes suivantes, (4) lecture normale et stockage dans la mémoire du PC des N lignes suivantes, (5) le cycle reprend au point 1 autant de fois qu'on le désire. A chaque cycle on enregistre dans la même image CCD une imagette de l'objet. Voici ce que cela donne dans le cas de Saturne (foyer direct d'un C8 et caméra Audine KAF-0400E non refroidie) :

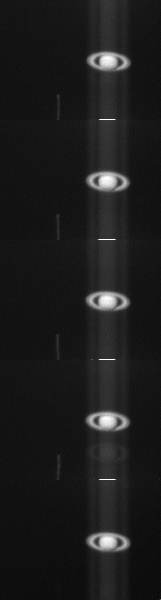
A gauche, le temps de pose est de 1 seconde par imagette (noter la présence de satellites et la forte saturation de la planète). Au centre, le temps de pose est de 0.075 seconde (le signal couvre toute la dynamique de la caméra, soit 15 bits). A droite, le temps de pose est de 0.01 seconde. Dans cette dernière image le smearing commence à apparaître, mais n'est pas strictement rédhibitoire encore. On voit qu'avec une caméra CCD astronomique qui autorise un pilotage très fin du fonctionnement (c'est le cas de l'Audine) il est possible d'obtenir un comportement proche d'une webcam, avec de la souplesse en plus (modification aisée du temps de pose par exemple). On peut souligner aussi qu'il n'y a pas de pièces en mouvement qui sont susceptibles de produire des vibrations ou s'user suite à un usage intensif. Mais attention, la principe du mode vidéo fait qu'il ne fonctionne que pour l'observation d'objets ponctuels ou de petites tailles (planètes). Il n'est pas question d'obtenir par cette méthode une image de la Lune ou du Soleil. La commande dans Iris qui permet d'acquérir de cette manière s'appelle VIDEO.

Une fois la bande d'imagettes acquise, elle est découpée pour produire des images individuelles, qui peuvent êtres traitées ensuite de manière traditionnelle. Il est en particulier possible de sélectionner sévèrement les meilleures images avant compositage. Il y a aussi la possibilité de recentrage des images avant la composition finale, ce qui est équivalent à compenser une partie de la turbulence atmosphérique (terme de tilt). Ces propriétés (sélection, recentrage) constituent des arguments forts pour expérimenter cette procédure d'observation vidéo. La commande qui permet d'extraire les imagettes s'appelle VIDEO_EXTRACT.

La syntaxe de la commande VIDEO est :

VIDEO [x1] [x2] [temps d'intégration] [taille d'un bloc] [nombre de blocs]

Les paramètres [x1] et [x2] définissent une zone suivant l'axe horizontal qui servira à produire l'image finale. Plus la largeur est réduite, plus rapide est l'acquisition.

Le temps d'intégration est en secondes.

On donne ensuite la hauteur d'un bloc élémentaire (valeur de N dans la description précédente).

Le nombre de blocs est le nombre d'imagettes souhaitées.

Exemple :

VIDEO 190 260 0.075 120 130

Vous pouvez interrompre l'acquisition à tout moment avec le bouton rouge de la barre d'outil.

Compte tenu du mode de lecture, il faut positionner d'une manière particulière l'objet étudié sur la surface du CCD. Vous devez par la pensée diviser le CCD suivant l'axe vertical en bande de N lignes de large et positionner l'image de la planète comme indiqué dans la figure suivante :

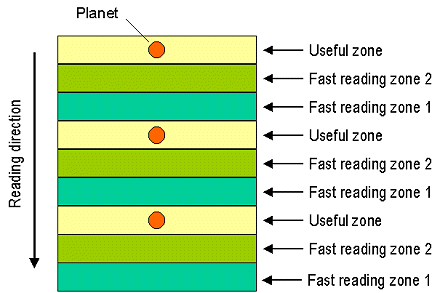
Pour vous aider à positionner l'objet la commande VIDEO_GRID trace dans l'image courante les bandes en question avec la largeur souhaitée. Par exemple :

VIDEO_GRID 120

La syntaxe de la commande VIDEO_EXTRACT est :

VIDEO_EXTRACT [nom] [hauteur] [premier index]

La paramètre [nom] est le nom générique des images extraites. [hauteur] est la largeur des imagettes. [premier index] est l'indice de la première image de la séquence. Exemple :

VIDEO_EXTRACT SAT 120 1

Petit rappel : pour le recentrage des images de la planète Saturne, qui a un contour assez complexe, la bonne procédure est la suivante (on suppose que le nom générique de la séquence est SAT et qu'il y a 50 images a traiter ) :

(1) Augmenter au besoin la taille de l'image en ajoutant des pixels autour (image de 256x256 pixels par exemple)...

PADDING2 SAT I 256 256 50

(2) Isoler la planète dans une image plus petite en faisant en sorte que le disque soit en gros centré. Pour cela avec la souris, définir un petit rectangle qui encadre le disque (c'est le centre du rectangle qui compte et non pas sa taille), puis faire (les images auront à présent une taille de 128x128 pixels avec Saturne au centre)...

WINDOW4 I J 128 50

(3) Normaliser le fond de ciel à zéro. Vous devez définir à la souris une zone rectangulaire (30x30 pixels de large typiquement) dans laquelle Iris va calculer le niveau du fond de ciel. Noter que depuis la version 3.51 de Iris, la commande NOFFET3 effectue ce traitement en donnant une valeur nulle à tous les pixels qui ont une intensité négative (cela améliore la précision de la commande PREGISTER à suivre)...

NOFFET3 J J 0 50

(4) Enfin, recentrer toutes les images par rapport à SAT1. La séquence K1, K2,... K50 contient le résultat du traitement :

PREGISTER J K 128 5

Nota : si vous souhaitez effectuer une sélection des meilleures images avec les commandes BESTOF ou BESTOF2, il est recommander d'effectuer l'opération avant le recentrage décrit précédemment pour éviter des problèmes de lissage qui peuvent amenuiser la précision de la sélection.

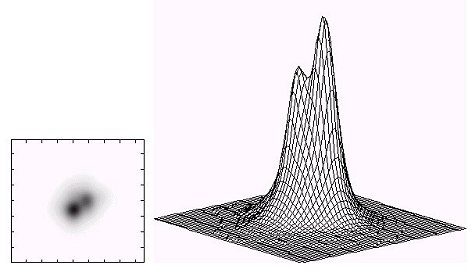
A titre d'illustration des possibilités du mode vidéo voici quelques résultats obtenues sur des étoiles.

La séquence ci-après, réalisée sur l'étoile Espilon 2 Lyre, montre tout l'intérêt de sélectionner. Dans cet extrait on note les méfaits de la turbulence qui produit une explosion sur toutes les images, sauf... une, vers le centre. Cette dernière sera extraite de la séquence et additionnée avec quelques autres bonnes images de l'objet. Suivant le degré de turbulence ou la taille du télescope, seulement 1% à 5% de la totalité des prises de vue sont conservées.

Par intermittence il est possible d'obtenir des images limités par la diffraction, comme le montre l'image ci-après de l'étoile Epsilon 2 Lyre sur laquelle on peut voir les anneaux de la tache d'Airy (télescope CN-212, caméra Audine en mode vidéo, temps de pose de 35 millisecondes et échantillonnage de 0,25 seconde d'arc par pixel). Le cercle intérieur marque la position du premier anneau noir de la tache d’Airy qui a un diamètre de 1.66 seconde d'arc avec la configuration optique utilisée. Le cercle extérieur donne la position du second anneau noir qui a un diamètre 3.05 secondes d'arc. Noter un résidu de coma dans l'image.

Ci-dessous compositage d'un douzaine de bonnes images de l'étoile Epsilon 2 Lyre avec ces composantes de magnitudes 5.1 et 5.4 et une séparation de 2.28". Le FWHM (= largeur à mi-hauteur = seeing) mesuré est de 0,75" alors que le FWHM de la tache de diffraction théorique est de 0,66’’. Télescope de 212 mm de diamètre avec obstruction de 0,33 (Takahashi CN-212).

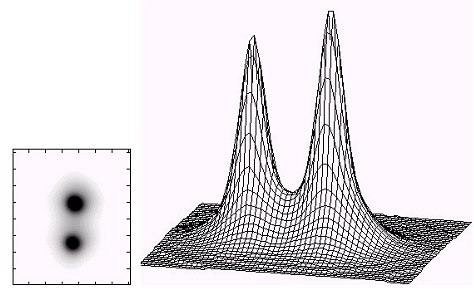
Le document ci-après montre dans les mêmes conditions de prises de vue (site urbain fortement turbulant) le couple S2751 avec une séparation angulaire de 1.6" et des magnitudes de 6.1 et 7.1. Le temps de pose est ici de 140 millisecondes. Une séquence 640 images a été acquise, d’où a été extrait 14 images de qualité qui ont permis de synthétiser ce résultat.

Quelques formules pour finir qui permettent de quantifier la turbulence et d'estimer la probabilité d'obtenir de bonnes images dans une séquence.

D'après D. Fried (JOSA 1978, 68, 1651) la probabilité P d'obtenir une bonne image dans une atmosphère turbulente est donnée par :

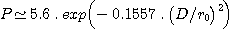
Le critère de bonne image est ici que la phase du front d'onde ne varie pas de plus 1 radian sur le diamètre D de la pupille du télescope. Le paramètre r0 est dit paramètre de Fried et défini le degré de turbulence (c'est en gros la taille des structures turbulente projetée à l'entrée du télescope, plus précisément la dimension pour laquelle l'erreur RMS du front d'onde atteint 0.4175 fois la longueur d'onde, c'est encore la définition du diamètre de cohérence de l'atmosphère). Avec D=21.5 cm et une probabilité P de bonne images de 5 sur 100, typique de mon site, soit P=0.05, on trouve au moment de l'observation environ r0 = 4 cm. C'est une très petite valeur, qui indique la présence de très nombreuses cellules de turbulences présentent simultanément à l'entrée du télescope. Le site est très mauvais, mais il est possible parfois d'observer la tache de diffraction grace à la technique des poses brèves... Dans les bons sites d'observation (haute montagne) la valeur de r0 est typiquement de 20 cm, mais peut atteindre 50 cm voit même plus.

Un autre moyen d'estimation de la turbulence consiste à mesurer la rapport de Strehl de l'image stellaire : c'est le rapport du signal concentré dans le premier disque d'Airy de la tache de diffraction (zone délimitée par le premier anneaux noir) dans le cas d'une optique altérée par des aberrations (turbulence par exemple) par le signal concentré dans ce même disque pour une optique parfaite. La rapport de Strehl (S) est donc au mieux égal à 1 (cas d'une imagerie limitée par la diffraction).

On montre que dans le cas d'une optique parfaite le télescope focalise 84% du signal dans le premier disque d'Airy (le reste du signal est distribué dans les anneaux extérieurs de la tache image). Une obstruction centrale de 0.33 dans le cas d'une optique de télescope rejète une partie plus importante du signal vers l'extérieur de la tache image, si bien que l'on ne retrouve plus que 70% du flux dans le premier disque. Dans ce cas, le rapport de Strehl n'est plus que S = 0.70/0.84 = 0.83.

On rappelle que le rayon du premier anneau noir de la tache de diffraction dans un télescope idéal est donnée par :

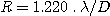
avec l la longueur d'onde. En adoptant l = 0.5 micron et D=212 mm, on trouve :
R = 2.88.10-6 rd = 0.59 seconde d'arc.

La présence d'une obstruction centrale, on la vue, modifie légèrement l'aspect de la tache d'Airy. Ainsi, lorsque l'obstruction centrale est de 0.33 (valeur typique dans les télescope Schmidt-Cassegrain), le rayon du premier anneau noir est donnée par :

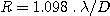
La taille de la tache de diffraction diminue donc au fur et à mesure que l'obstruction centrale augmente. La résolution augmente donc lorsque que la taille du miroir secondaire croit, ce qui peut paraître paradoxal. Mais la redistribution du signal dans les anneaux complique l'interprétation de la notion de résolution dans ce cas.

Dans IRIS vous pouvez créer une étoile artificielle ayant la forme d'une tache d'Airy en utilisant la commande DRAW_AIRY. La syntaxe est :

DRAW_AIRY [TAILLE] [I0] [DIAMETRE] [OBSTRUCTION] [LAMBDA] [ECHELLE]

avec :

[taille] : la dimension de la nouvelle image en pixels (le format est carré)
[I0] : l'intensité au pic de la tache d'Airy en ADU
[diamètre] : le diamètre du télescope en millimètres
[obstruction] : le rapport d'obstruction du miroir principal (rentrer 0 pour un télescope sans secondaire)
[lambda] : la longueur d'onde en microns
[échelle] : l'échelle de la taille de la tache image en seconde d'arc par pixel.

Noter que la commande produit le fichier texte AIRY.DAT dans le répertoire de travail qui contient le profil de la tache d'Airy sous une forme tabulée.

Par exemple pour une télescope Celestron 8 vous ferez par exemple (voir une application plus loin) :

DRAW_AIRY 100 30000 200 0.33 0.65 0.15

Un instrument optique répondant au critère de Rayleigh présente une défaut du type aberration sphérique sur l'onde d'une amplitude totale de l/4. La valeur de l'erreur RMS sur l'onde correspondante est 3.5 fois plus faible (définition de Maréchal), soit ici s = 0.25/3.5 = 0.071 . l (l'erreur RMS s'exprime ici en unité de longueur). Il existe une relation entre l'erreur RMS sur l'onde et le paramètre de Strehl :

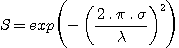
Le terme à situé dans la parenthèse est l'erreur de phase en radian. Avec s = 0.071 . l on trouve :

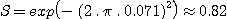
De la même manière, vous pouvez calculer qu'une optique à l/4 a un rapport de Strehl de 0.97 (en absence d'obstruction centrale), et ainsi de suite (la formule précédente est valide jusqu'à des valeurs de S>0.2). Au dessus d'un rapport de Strehl de 0.8 la performance du système optique est considérée comme étant limitée par la diffraction.

La relation entre l'erreur RMS de phase (en radian) et le paramètre r0 est donnée par :

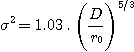
On calcule ensuite le paramètre de Strehl par la formule habituelle (avec l'erreur sur la phase en radian) :

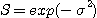
On vérifiera aisément que S=0.36 lorsque le diamètre de cohérence de l'atmosphère est égal au diamètre du télescope (D = r0)

Les relations précédentes montrent la mesure du paramètre de Strehl est un très bon traceur de la valeur de la turbulence.

Avec IRIS, l'énergie encerclée dans le premier anneau théorique de la tache image et l'énergie à l'extérieur de l'anneau peuvent être aisément mesurée avec la fonction d'analyse photométrique PHOT (photométrie d'ouverture). Au besoin, pour accroître la précision, vous échantillonnerez plus finement l'étoile en utilisant la commande ASCALE (cette fonction conserve les caractéristiques photométriques de l'image).

La largeur à mi-hauteur (FWHM) de la tache d'Airy d'un instrument parfait est donnée par la relation :

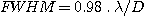
En présence de turbulence et pour une pose longue (quelques secondes et plus), on aura :

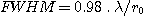
La mesure du FWHM observé sur une étoile posée plusieurs secondes (c'est la valeur du seeing) et sa comparaison avec le FWHM théorique donne immédiatement la valeur de r0 :

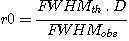
Pour mon instrumentation le FWHM typique en longue pose est de 2.5 secondes d'arc. Tout calcul fait, on trouve un r0 correspondant de 4 cm, ce qui confirme la valeur déjà trouvée par la statistique du nombre d'images satisfaisantes dans un lot.

En longue pose nous avons aussi :

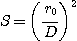
On voit que dans notre exemple, en longue pose, le rapport de Strehl n'est que de 0.035. Le fait de faire des poses courtes et de sélectionner soigneusement les images à additionner permet d'augmenter ce chiffre d'un bon ordre de grandeur. C'est tout l'intérêt de travailler en mode vidéo ou avec des webcam dans l'objectif de pratiquer des poses brèves à une cadence de plusieurs images par seconde.

L'image suivante montre l'étoile double Gamma Andromède (observée de 15 octobre 2001), dont les composantes A et B, de magnitudes respectives 2.3 et 5.1, sont séparées d'une distance de 9.87". L'instrument utilisé est un C8 avec un agrandissement de l'image par une barlow Televue 5x. L'échelle est de l'image 0.151"/pixel, ce qui permet d'échantillonner correctement l'image de l'étoile. Un filtre rouge (bande R du système BVR) est interposé pour réduire les effets de la réfraction atmosphérique et avoir une tache de diffraction mieux définie. La caméra est une Audine utilisée en mode vidéo avec un temps de pose de 50 millisecondes. La nuit était turbulente avec un vent sensible, ce qui ne pardonne pas ici. 20 images sur un totale de 400 ont été sélectionnées et compositées pour produire le document final. Pour parfaire la visualisation et voir à la fois les anneaux et le coeur de la tache de diffraction une visualisation logarithmique a été appliquée au résultat final. En médaillon, une image artificielle d'étoile, générée avec la commande DRAW_AIRY, a été ajoutée.

Le premier anneau est visible (noter la conformité avec le modèle tracer avec les paramètres de l'instrument, C8 avec obstruction centrale de 0.33 et longueur d'onde de 0.63 micron). Un autre anneau plus extérieur est aussi aperçu.

Les meilleures images de la séquence ont été sélectionnées avec la commande BEST_STREHL (depuis IRIS V3.52a), qui a pour syntaxe :

BEST_STREHL [NOM] [NOMBRE]

Le principe de fonctionnement est identique à celui de la commande BESTOF pour l'imagerie planétaire. Simplement ici, le critère de sélection est l'intensité maximale du pic de l'étoile (plus celui-ci est élevée, meilleure est généralement l'image).

La commande BEST_STREHL s'utilise avec la commande SELECT pour isoler les meilleures images. La registration est effectuée en utilisant REGISTER et enfin le compositage final en utilisant ADD_NORM (qui permet de ne pas saturer le pic de l'étoile).

Pour incruster l'étoile artificielle on utilise DRAW_AIRY, puis PADDING pour harmoniser les tailles d'images, la translation pour positionner l'étoile artificielle où on le souhaite (TRANS) et enfin une simple addition pour associer l'image réelle et l'image artificielle (ADD).

La syntaxe de DRAW_AIRY est :

DRAW_AIRY [taille de l'image] [Intensité au centré] [diamètre télescope (mm)] [obstruction] [lambda (micron)] [échelle (arcsec/pixel)]

Pour notre exemple on fera :

draw_airy 100 10000 200 0.33 0.63 0.151

Nota : pour avoir une vue spectaculaire de la tache d'Airy, faite le logarithme de l'image calculée avec DRAW_AIRY :

LOG 10000

Le calcul du rapport de flux dans le premier anneau par le flux total dans la tache image (commande PHOT) montre que le rapport de Strehl atteint 0.38 dans le document précédent, ce qui est honnête compte des conditions atmosphériques pas vraiment adaptées à l'imagerie haute -résolution (en de très bref instant le paramètre r0 atteint ici 200 mm, voir les formules précédentes). On note par ailleurs une asymétrie dans la forme de l'anneau qui est le signe d'un léger problème de collimation optique.