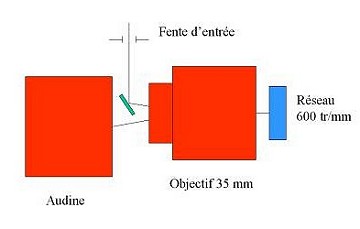
3. TEST DE LA VERSION BASSE RESOLUTION
Le versin basse résolution comprend essentiellement un réseau Edmond Scientific de 600 traits/mm de 30 mm de coté utilisé en montage Littrow et un objectif photographique de 35 mm de focale (Nikon à F/2), servant à la fois de collimateur et d'objectif de chambre. La caméra CCD est une Audine équipée d'un KAF-0401E. La dispersion spectrale est de 4.0 angstroms par pixel (pixels de 9 x 9 microns).
Le prétraitement des spectres a été effectué avec Iris et l'exploitation avec le logiciel VisualSpec de Valérie Desnoux.
Pour les tests le spectrographe est monté à l'arrière d'une lunette FSQ-106 de Takahashi de 106 mm d'ouverture et de 530 mm de focale. La monture est une EM200. C'est équipement est quelque peu luxueux et il est clairement possible de travailler avec un matériel plus modeste. Le seul paramètre à bien maîtriser est la finesse des étoiles au foyer du télescope car c'est d'elle dont dépend en partie la résolution spectrale finale dans un spectrographe à fente large. Si cela est possible, il faut chercher à réduire la focale du télescope car alors la dimension linéaire de l'étoile au foyer est plus petite, ce qui est tout bénéfice pour la résolution. Une réducteur de focale sera donc un accessoire utile, notamment avec des télescopes ouvert à F/10. Il faut cependant que le rapport F/D soit supérieur à 4 pour ne pas diaphragmer le faisceau du télescope à l'intérieur du spectrographe (nota, inversement le spectrographe R=10000, autorise uniquemernt des faisceaux arrivant du télescope moins ouvert que f/8).
Schéma
de principe tout métal en bas.




Situation du lieu d'observation, particulièrement pollué, notamment par un éclairage constitué de lampes au sodium. Noter l'usage du comparateur pour une focalisation précise. La lunette est un quadruplet fluorine donnant de très bonnes images, avec un chromatisme particulièrement faible.
Les spectres de la version basse résolution présentent une courbure significative et il a été nécessaire d'adapter le logiciel d'extraction du profil spectral à cette situation. Une procédure de calibration spécifique sera décrite plus loin.

Spectre de l'étoile 54 Oph. L'axe de la dispersion est horizontal et le domaine spectral va de 4500A à 7500 A environ. On note que le spectre n'est pas rectiligne, le rayon de courbure étant ici de 29000 pixels. Une fonction spéciale dans Iris permet de réaliser un binning pour calculer le profil spectral qui tient compte de cette courbure (les deux courbes centrales qui encadrent le spectre). Les courbes les plus extérieures délimitent une zone dans laquelle le niveau du fond de ciel est déterminé.
Une particularité de ce spectrographe est d'autoriser un mode d'imagerie directe (sans dispersion de la lumière) en orientant le réseau de manière à ce que l'ordre zéro soit confondu avec l'axe optique principal. En utilisant une fente large, cela permet d'identifier le champ (environ 10% du flux incident est alors utilisé). Il est aussi possible d'exploiter l'image d'ordre zéro pour réaliser la calibration spectrale des spectres, ainsi que la calibration radiométrique (voir plus loin). Lors des tests, cette disposition c'est avéré extrêmement pratique et efficace grace à l'adoption d'un dispositif mécanique précis d'orientation du réseau.
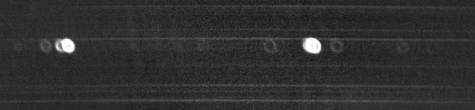

A haut, le spectre dans l'ordre 1 de la nébuleuse M57. A bas, l'image à l'ordre zéro correspondante. Remarquer la relation entre la position des étoiles et leur spectres. Sur l'image d'ordre zéro on devine le contour vertical de la fente large (non parfaitement focalisée ici).
3.2. Calcul du rendement ou throughput
La courbe ci-après montre le rendement global de l'instrument utilisé (ou throughput en anglais). Ce rendement est le rapport du nombre de photoélectrons produits dans un élément spectral (1 pixel) à une certaine longueur d'onde par le nombre de photons pénétrant dans l'instrument pour la longueur en question.
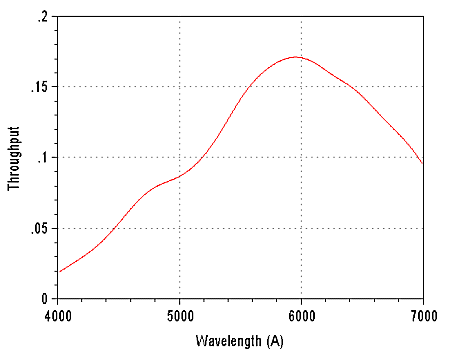
Rendement total du spectrographe, de la lunette et du détecteur. La transmission atmosphérique est aussi prise en compte.
Le rendement de l'instrument est maximal vers la longueur d'onde de 600 nm et atteint 17%, ce qui est un bon chiffre pour un spectrographe. La courbe a été tracée à partir de l'analyse du spectre de l'étoile Véga, de type A0V.
Voici comment est déterminé un point de cette courbe. A la longueur d'onde de 6000 angstroms, l'étoile Véga produit hors atmosphère un éclairement spectral de 845 photons/cm2/s/A (voir plus loin une expression qui permet de calculer cette valeur). Le diamètre de la lunette étant de 10.6 cm, la surface collectrice est de 88.2 cm2. Le flux pénétrant dans un instrument hors atmosphère est donc de :
845 x 88.2 = 74529 photons/s/A
L'intervalle spectral sous-tendu par un pixel compte tenu de la dispersion est de 4 angstroms. Le flux photonique provenant d'un instrument parfait dans un pixel est alors :
74529 x 4 = 298116 photons/s
Le temps d'exposition utilisé pour observer Vega est de 1.7 seconde (au-delà, le détecteur est saturé). Dans ce laps de temps il arrive donc sur le détecteur :
298116 x 1.7 = 506797 photons
Par ailleurs, on mesure après binning que le signal dans l'image du spectre de Véga à la longueur d'onde de 6000 angstroms est de 43213 ADU après 1.7 secondes de pose. Compte tenu du gain de la caméra Audine utilisé, qui est de 2 électrons par ADU, on en déduit que le nombre total d'électrons dans un pixels lors de l'observation d'une étoile de magnitude zéro, de type spectral A0V et pour un temps d'intégration de 1.7 seconde est de 2 x 43213 = 86427 électrons.
La valeur théorique du signal calculée plus haut étant de 506797 électrons pour un instrument parfait, on en déduit un rendement de l'instrument (incluant l'atmosphère) à la longueur d'onde de 6000 A de 86427 / 506797= 0,17 = 17%.
A cette longueur d'onde le rendement quantique du CCD est de 61%, ce qui permet de calculer que le rendement de l'optique seule (et de l'atmosphère au moment de l'observation) est de 28%. Le rendement du réseau utilisé est lui même de 62% à 600 nm. Le reste de l'optique représente donc une transmission d'environ 45%, un chiffre que l'on retrouve bien par calcul en prenant en compte les pertes de flux dans les divers dioptres traversés (nombreux en raison de l'usage d'un objectif photographique) et l'atténuation de l'atmosphère. Noter la disponibilité d'une feuille Excel qui facilite ces calculs.
Page index page Page précédente Page suivante