3.4. Calcul du rapport signal sur bruit

L'image suivante montre un test de magnitude limite. L'étoile observée (dans le champ de M57) est de magnitude 10.5. Le rapport signal sur bruit mesuré sur le profil spectral est de 6 pour un temps de pose de 9 minutes et une ouverture de 106 mm. Le paramètre qui contraint le plus la détectivité ici est la brillance du niveau de fond de ciel, particulièrement élevée dans le lieu d'observation (résidence largement éclairée par des lampadaires boules au sodium). Une fente moins large (de l'ordre de 1 mm au lieu des 5 mm actuels) aurait permis de diminuer significativement le niveau du fond de ciel, tout en rendant le centrage de l'objet encore relativement simple.

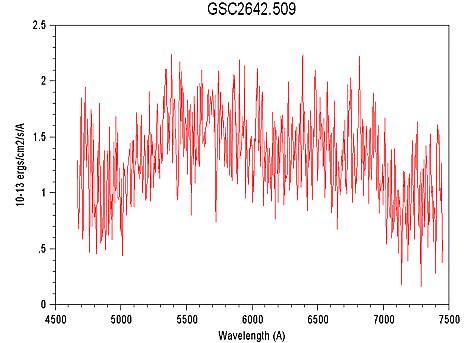
Pose cumulée de 9 minutes d'une étoile de magnitude 10.5.
Le signal est ici calibré en valeur physique (en ergs/cm²/s/A).

Nous allons vérifier par simulation numérique la valeur de ce rapport signal sur bruit vers la région de la raie H-alpha à 6563 angstroms.

Soit E₀(l) l'éclairement spectral hors atmosphère d'une étoile de magnitude V=0 et de type spectral A0V. Nous allons effectuer le calcul pour la région du spectre correspondant à la raie H-alpha. Cet éclairement s'exprime en nombre de photons par centimètre carré, par seconde et par angstrom (ou en abrégé : photons/cm²/s/A). La valeur numérique est donnée par la formule suivante :

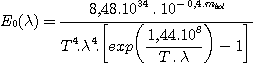
avec :

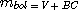
et :

l = longueur en angstrom pour laquelle on désire connaître l'éclairement = 6563 A (longueur d'onde de la raie H-alpha)

T = température effective de l'étoile = 10800 K (pour une étoile A0V)

BC = correction bolométrique = -0,4 (pour une étoile A0V).

Le calcul donne E₀(6563) = 733 photons/cm²/s/A.

Soit N₀(l) le nombre d'électrons par seconde dans un élément spectral pour une étoile de magnitude V=0 (l'élément spectral est délimité par la taille du pixel suivant la direction de la dispersion). On a :

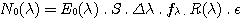
avec :

E₀(l) = 733 photons/cm2/s/A pour l = 6563 A.

S = surface collectrice du télescope = 88,2 cm² (pour la FSQ-106 qui a un diamètre d'objectif de 10,6 cm, dans le cas d'un télescope, il faut tenir compte de l'obstruction centrale)

Dl = valeur de l'échantillonnage spectral pour un pixel = 4 angstroms par pixel avec un réseau de 600 traits/mm, un objectif de 35 mm de focale et des pixels de 9 microns de coté.

f_l = facteur de binning dans le CCD pratiqué lors l'acquisition suivant l'axe de la dispersion. Pour les tests on n'a pas fait de binning afin de conserver la résolution spectrale maximale, d'où f_l=1.

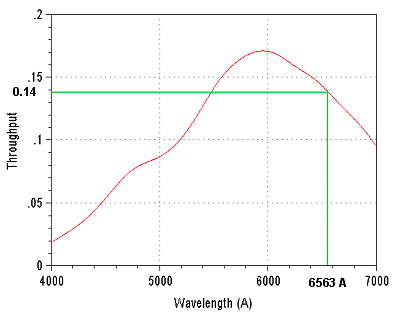
R(l) = rendement de l'instrument (throughput) qui inclue ici la transmission atmosphérique typique, la transmission de la lunette, le rendement du spectrographe et le rendement quantique du CCD.

Nous adoptons R(6563) = 0,14 (voir figure ci-après).

e = fraction du signal total de l'étoile prise en compte lors du binning dans la direction spatiale pour construire le profil spectral (binning dans la direction perpendiculaire à la dispersion). Nous considérons ici que le binning est suffisant large (7 pixels) pour intégrer tout le flux stellaire, aussi e = 1.

Avec les valeurs numériques on trouve N₀(6563)= 733 . 88,2 . 4 . 1 . 0,14 . 1 = 436200 électrons/s.

Signalons que dans le cas de l'observation d'une source diffuse (spectre d'une galaxie par exemple) le signal par unité de temps (en électrons/secondes) est donné par :

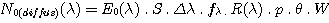
avec cette fois E₀(l) la brillance de surface de l'objet (luminance) en électrons/cm²/s/A/arcsec et :

p = le nombre de pixel intégré dans la direction spatiale (direction perpendiculaire à la dispersion).

q = l'échelle angulaire par pixel suivant la direction spatiale = 3,5 seconde d'arc par pixel dans le cas de la FSQ-106 utilisée avec une Audine.

W = la largeur angulaire de la fente d'entrée du spectrographe (en seconde d'arc).  

Le rapport signal sur bruit (S/B) est donné par la formule :

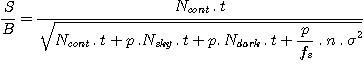
avec :

N_cont = signal en électrons par seconde dans le continuum pour une étoile de magnitude m. Cette quantité ce déduit de la formule :

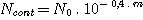
Ici nous avons m=10,5, soit N_cont=2,28 électrons/s.

N_sky = le signal moyen du fond de ciel sous le spectre en électrons par seconde et par pixel. Cette quantité est relevé directement depuis une image posée relativement longtemps pour rendre la mesure précise. On trouve N_sky=10 électrons/s pour le site d'observation (très pollué), une fente très large de 970 secondes d'arc et une région de l'image qui exclue les raies spectrales importantes de l'éclairage artificiel (au sodium pour l'essentiel). Au niveau des raies spectrales de l'éclairage urbain le fond de ciel est 4 fois plus élevé.

N_dark = signal d'obscurité du CCD en électrons par seconde. L'analyse statistique d'images faites dans l'obscurité montre que le taux de signal d'obscurité est de 0,3 électron/seconde dans les conditions 'utilisation de la nuit d'observation.

p = largeur en pixel de la zone du binning suivant l'axe perpendiculaire à la dispersion pour calculer le profil spectral (nombre de pixels additionnés). La valeur adoptée (p=7 pixels) est caractéristique pour intégrer tout le flux stellaire significatif pour des étoiles faibles.

f_s = le facteur de binning au sein du CCD suivant l'axe spatial (perpendiculaire a la dispersion). Pour les tests aucun binning interne dans le CCD n'a été pratiqué, d'où f=1.

s = bruit de lecture par pixel de la caméra Audine = 18 électrons

t = temps de pose total = 540 secondes dans notre exemple (compositage de 9 poses d'une minute chacune)

n = nombre d'images compositées pour atteintre le temps de pose t = 9

Nous avons alors :

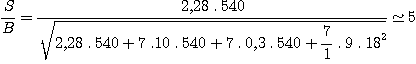
On retrouve bien approximativement la valeur déterminée expérimentalement.

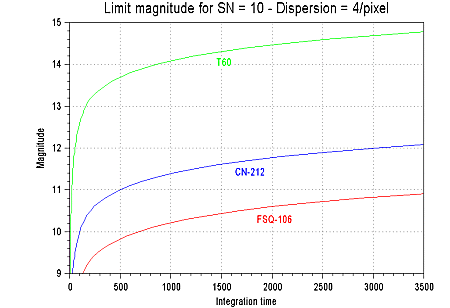
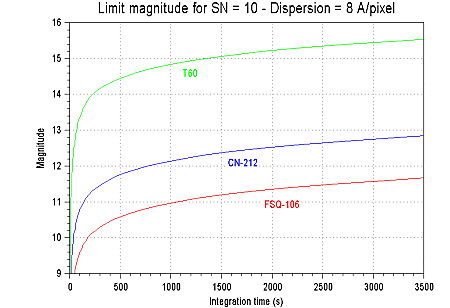
Les graphes ci-après montre la magnitude limite atteinte avec divers instruments pour un rapport signal sur bruit sur le continuum de 10, suffisant pour effectuer certaines mesures astrophysiques et reconnaître un type spectral.

Magnitude limite pour un S/B de 10 et une dipersion de 4 A/pixel en fonction du temps de pose (en secondes) au voisinage de la raie H-alpha pour une étoile de type A0V. Les conditions du calcul sont : pour la FSQ-106, p=7 et N_sky=10e^-, pour le CN-212 (télescope Takahashi en version Newton) p=10 et N_sky=10e^-, pour le T60 (télescope de 60 cm du Pic du Midi) p= 12 et N_sky= 2.5 e^-. Dans tous les cas le temps de pose total est segmenté en poses élémentaires de 180 secondes.

Même condition que ci-dessus, mais pour une dispersion de 8 A/pixel en faisant un binning d'un facteur deux suivant l'axe de la dispersion (f_l=2). Le gain en détectivité est d'environ une magnitude.

Une variante du calcul permet de prédire le résultat de l'observation de spectres comportant des raies en émission. Cette situation est particulièrement courante avec les étoiles Be et systématique par exemple dans les spectres de novae ou de quasars. L'intensité de la raie est alors donnée par la largeur équivalente W. Dans une étoile Be en émission relativement modérée on a W=5 angstroms (pour un quasars et la raie H-alpha on peut adopter W=200 angstroms, ce qui signifie une raie très intense par rapport au continuum, et ce qui permet du reste de faciliter la détection de ces d'objets).

L'intensité de la raie en émission est donnée par :

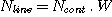
Soit pour notre étoile de magnitude 10,5, N_line=2,28 . 5 = 11,4 électrons/s

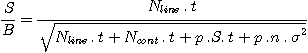
Le calcul donne :

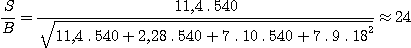
Un tel rapport signal sur bruit au niveau de la raie d'émission rend son observation relativement facile pour une étoile de magnitude 10,5. Un tel spectre d'émission est détectable jusqu'à la magnitude 11,5 avec une lunette de 100 mm d'ouverture seulement. La performance est encore meilleure sous un ciel bien noir ou/et avec une fente plus fine (le bruit du fond de ciel est ici le terme de bruit dominant).

Pour illustrer les propos précédent, la figure ci-après montre la détection de l'émission de la raie H-alpha dans le quasar 3C273 réalisée avec un télescope CN-212 (diamètre du miroir de 212 mm), Le miroir du télescope, utilisée en mode Newton à F/D=3.9, était légèrement diaphragmé par le spectrographe à un diamètre équivalent de 185 mm. La caméra est une Audine exploitée en binning 2x2 (dispersion de 8 angstroms par pixels). Le temps de pose est de 36 minutes (compositage de 12 poses de 3 minutes chacune). Il est à noter que le ciel, en plus d'être pollué par la lumière de l'éclairage urbain (magnitude limite a l'oeil de 2.5), était constellé de cirrus au moment de l'observation (13 mai 2001). La longueur d'onde mesurée de la raie H-alpha est de 7598 A (la mesure est facilité par la présence dans le champ de l'étoile de magnitude 10,7 qui montre des raies de Balmer bien nettes). Le décalage vers le rouge correspondant est de 0,158, ce qui est exactement la valeur attendue à partir de l'information des catalogues.

A haut, le champ du quasar 3C273 observé dans l'ordre zéro (pose de 3 minutes). En bas , le spectre de tous les objets de ce champ. Noter qu'une étoile voisine ne gène pas l'analyse du spectre de 3C273. Le continuum est très faible au voisinage de la raie H-alpha mais cette raie est bien visible du fait de son émission. A signaler encore qu'une étoile de magnitude 12.9 produit un spectre lisible. Télescope CN-212 et spectrographe utilisé avec une dispersion de 8 A/pixel. Temps de pose total de 36 minutes le 13.1/05/2001.

3.5. Calibration

Les procédures de calibration des spectres ont fait l'objet d'une attention particulière lors du travail sur ce prototype (voir le chapitre xxx pour une description détaillée). La partie la plus délicate est la correction flat-field (uniformisation du gain en tout point de l'image CCD). La difficulté en spectrographie provient du fait qu'une plage de lumière uniforme servant à illuminer la surface du détecteur et permettant de déterminer les coefficients de correction a un contenu spectral plus ou moins connu. L'image de calibration flat-field observée est ainsi le produit d'une image dépendant de la longueur d'onde (en raison de la signature spectrale de la source et du throughput spectral de l'instrument) et d'une image dépendant du vignettage (dans ce dernier terme nous incluons aussi la variation relative de sensibilité de pixel à pixel). Le problème est de séparer ces deux images. Une partie de la solution consiste à utiliser une source lumineuse illuminant la hauteur de la fente et dont le spectre est bien connu. C'est souvent une lampe à incandescence qui est utilisée pour cela, mais ce type de solution c'est avéré problématique à mettre en oeuvre avec le Littrow basse résolution et à fente large. Une raison possible est un mauvais bafflage du spectrographe, problème qu'il faudra résoudre par la suite. Les parois interne du prototype ne sont pas peintes en noir ce qui ne facilite pas non plus la calibration radiométrique du fait de la présente de réflexions parasites. En fin de compte, la procédure qui a donné le meilleur résultat consiste à profiter de l'image d'ordre zéro (image directe non dispersée du champ) pour déterminer le vignettage optique (la fente doit alors avoir la même largeur que la surface sensible du CCD), puis à observer une ou plusieurs étoiles de spectre bien connu en mode spectrographe pour déterminer la sensibilité spectrale (cette dernière opération est à présent bien maîtrisée sous VisualSpec).

La procédure de calibration radiométrique prend aussi en compte la présence de la diffusion au sein du spectrographe, qui crée un terme d'offset pouvant être variable en fonction de la longueur d'onde. La diffusion est mesurée dans deux zones masquées de la fente, de part et d'autre de l'ouverture. La valeur adoptée est la moyenne de ces deux mesures. Ici encore, la fente va être modifiée pour faciliter cette mesure dans le futur.

Le problème de la calibration spectrale a aussi été étudié soigneusement. En effet, l'étendue spectrale couverte est telle qu'il n'est pas possible de considérer que l'on est en régime de dispersion linéaire (l'écart à la linéarité atteint près de 30 A d'un bout à l'autre du spectre). La loi de dispersion calculé est de la forme :

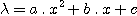
avec x la position dans l'image en pixel. Les paramètres a, b et c sont déterminé à partir de la mesure de 3 raies spectrales de longueur d'onde connue sous VisualSpec. L'erreur de calibration spectrale résiduelle est alors inférieure à 8 A de 4500 à 7500 A pour une dispersion de 4 A/pixel.

Les coefficients calculés pour le spectrographe actuel sont :

a = -1.4426.10^-4  ;   b = 4.114  ; c = 4470

Le terme c dépend de la position de l'étoile dans la fente large. La dispersion moyenne est de 4.00 A/pixel

Pour ce qui concerne l'extraction proprement dite du spectre et la soustraction du fond de ciel, nous l'avons vu, il faut tenir compte de la courbure des spectres. Ces phases du traitement vont être analysée au chapitre suivant.

3.6. Premières conclusions

Le version basse résolution du spectrographe Littrow testée révèle des caractéristiques proches du niveau théorique espéré. Le chromatisme de l'objectif photographique permet d'obtenir sans refocalisation des spectres corrects de 670 nm à 450 nm. La disponibilité de l'ordre zéro permet de calibrer spectralement avec une précision de 10 angstroms environ.

A partir d'un calcul théorique utilisant les résultats précédent, il apparaît que le spectrographe Littrow basse résolution exploité dans un ciel bien noir et en posant autour de 20 minutes devrait permettre d'atteindre avec un S/B de 6 la magnitude 15 sur un C11 et la magnitude 16.7 sur un télescope de 600 mm. Ce sont des résultats très prometteurs qui ouvrent bien des perspectives. Il devrait ainsi être possible de suivre un bon nombre d'étoiles variables avec des télescopes de ce diamètre, y compris des Mira, avec par exemple des mesures spectrophotométriques fines. Des novae pourront être étudiées sur des périodes longues. Il en est de même pour l'observation des comètes. Enfin, quelques supernovae deviennent la cible possible des amateurs avec une résolution spectrale de 800, très proche de ce que font les professionnels dans le domaine, ce qui laisse augurer des observations spectaculaires.

La principale amélioration à apporter à la version actuelle du spectrographe concerne la mise au point d'un système de fente réglable en largeur ou escamotable permettant d'interchanger rapidement des fentes. Cela s'avère nécessaire dans certaines situations (observation d'un objet étendu, tel une comète ou une surface planétaire), pour la calibration et constitue un moyen efficace pour lutter contre les méfaits de la pollution lumineuse, tout en gardant la facilité actuelle de pointage des objets. Cliquer ici pour voir un exemple type d'utilisation d'une fente fine (observation de la comète LINEAR A2).

Page index page                                Page précédente                                   Page suivante