Un stage de spectrographie astronomique

Stage de spectrographie - Session 4 (1/2)

L'ETALONNAGE DES DONNEES SPECTRALES

Aude - Je vous propose de passer à la phase d'étalonnage du spectre de l'étoile HD45677. Résumons la situation. Lors de la deuxième session nous avons effectué le prétraitement d'un ensemble d'images brutes du spectre de cette étoile. Après compositage des images individuelles, nous avons obtenu une image du profil spectral qui a été sauvegardée sur le disque sous le nom T45677_2.

Les spectres ont été acquis avec le spectrographe d'écrit lors de notre première session. On sait que la dispersion est de 2,9 angstroms par pixel environ.

Raymond - Tu nous as dit, Aude, au moment où on s'est quitté que nous allions utiliser à présent un logiciel spécialisé, mais spécialisé en quoi ?

Aude - En gros, les opérations que nous avons effectuées précédemment sur notre spectre sont assez classiques en traitement des images CCD astronomique : retrait de l'offset, du signal d'obscurité, division par le flat-field, registration, addition. Il y avait certes quelques opérations particulières, comme le recentrage des images sur des raies spectrales, la correction des distorsions géométriques ou encore le binning optimisé, mais bon, rien de vraiment très complexe. Le produit à la sortie de tous ces traitements est un profil spectral dans lequel l'axe des abscisses représente des numéros de pixels et l'axe des ordonnées un signal.

Les deux opérations qu'il nous reste à faire afin de pouvoir exploiter le spectre sont, d'une part l'étalonnage en longueur d'onde de l'axe des abscisses, d'autre part l'étalonnage en flux l'axe des ordonnées pour obtenir la vraie distribution spectrale de l'objet. Pour ce, faire je vous propose d'utiliser le logiciel VisualSpec dont le boulot est, entre-autre, de réaliser ces opérations.

Christian - On se le procure comment VisualSpec ?

Aude - Vous pouvez le télécharger sur le web à cette adresse : http://valerie.desnoux.free.fr/vspec. Il est gratuit. Mon but n'est pas de vous apprendre toutes les subtilités de VisualSpec. Je vais simplement vous donner quelques repères. Je ne saurais trop vous conseiller de lire le manuel de référence et d'utilisation fournis avec VisualSpec, et aussi de suivre quelques-unes des notices explicatives que vous pouvez consulter directement depuis le web. Par exemple : http://valerie.desnoux.free.fr/vspec/tutorial.html

Mais avant d'aborder les opérations d'étalonnages, je crains qu'il ne soit nécessaire de faire encore un petit tour avec Iris...

Alain - Comment cela, tu nous as dit que nous avions fini les opérations de prétrairement !?

Raymond - On nous aurait donc mentis !!??

Christian - C'est vrai ce bruit qui court Aude, tu nous cache des choses !!!

Aude - Mes amis, ça va être rapide. Mais c'est vrai, j'ai omis volontairement un détail important. Pour réaliser l'étalonnage en flux de l'étoile HD45677 il nous faut connaître la réponse spectrale de l'instrument. C'est une courbe qui nous informe, en fonction de la longue d'onde, comment l'ensemble de notre instrument atténue le flux en valeur relative. Par exemple, puisque le capteur CCD est plus sensible dans la partie rouge que dans la partie bleue du spectre, la réponse instrumentale sera plus faible d'un certain facteur dans le bleu que dans le rouge. Ce que nous devons calculer, c'est la valeur de ce facteur pour toutes les longueurs d'ondes.

Raymond - Mais je connais déjà la réponse du CCD, il me suffit de la prendre dans la notice du capteur !

Aude - Ca ne marche pas. Ce que tu va trouver c'est une réponse moyenne, mais il n'est pas exclu que ton propre CCD s'écarte sensiblement de cette moyenne. Quand bien même, dans l'instrument il n'y a pas que le CCD. On trouve le télescope, le spectrographe et même l'atmosphère. Tous ces éléments contribuent à moduler à leur manière la réponse de l'instrument.

Raymond - L'atmosphère ?

Aude - Oui, par exemple suivant la hauteur de l'astre étudié par rapport à l'horizon, la lumière est plus ou moins rougie, ce qui montre qu'il existe un effet spectral induit par l'atmosphère.

Christian - Il parait bien difficile de prendre en compte tous ces paramètres...

Aude - Ca l'est en effet, aussi est-il préférable d'évaluer la réponse de manière expérimentalement et le plus directement possible. J'ai donné brièvement la procédure à suivre lors de la deuxième session au moment de la discussion sur le flat-field. Je vais reprendre cela plus en détail.

La technique consiste à enregistrer au cours de la nuit le spectre d'une étoile dont on connaît bien le type spectral. Idéalement, il faut choisir une étoile standard spectrophotométrique pour laquelle le flux absolu par élément de longueur d'onde est connu en dehors de l'atmosphère terrestre. A partir de cette observation, nous allons faire correspondre le spectre observé et prétaité de l'étoile standard avec la valeur attendue du flux pour cette étoile. On obtient la réponse instrumentale en divisant le spectre observé par son spectre théorique.

Ensuite, pour calculer la vraie distribution spectrale dans l'étoile HD45677, il suffira de diviser sont profil spectral observé par la réponse instrumentale calculée précédemment

Tout ceci pour vous dire que la même nuit de l'observation de HD45677, j'ai fait le spectre d'une étoile que j'ai assimilé à une étoile standard, en l'occurrence Alpha Gémeaux, de type spectrale A1V. Ce que nous devons faire sous Iris, c'est tout simplement prétraiter le spectre de cette étoile.

Raymond - C'est assez complexe ces opérations, je ne suis pas sur d'avoir tout compris.

Christian - Heu, moi non plus (timide)...

Alain - Moi si !

Aude - D'accord, pour Raymond et Alain, je vais faire un ou deux schémas. Analysez les 3 graphiques suivants :

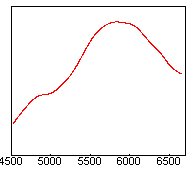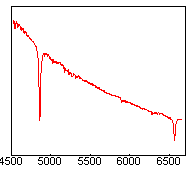
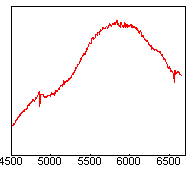
A gauche, vous avez le vrai spectre de l'étoile Alpha Gémeaux, tel qu'on pourrait l'observer depuis l'espace avec un instrument ayant une réponse absolument plate quel que soit la longueur d'onde. Ce spectre est caractéristique d'une étoile chaude de type spectral A, avec un continuum intense dans le bleu et des raies profondes de l'hydrogène.

Au centre nous avons la réponse globale de l'instrument en fonction de la longueur d'onde. C'est une donnée à priori inconnue.

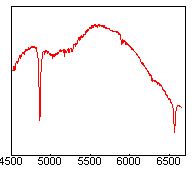
A droite, on trouve le spectre effectivement observé de l'étoile Alpha Gémeaux. C'est le produit de la vraie distribution spectrale de l'étoile par la réponse de l'instrument. On voit que les effets instrumentaux distordent considérablement la réalité, ce qui montre bien l'importance de la correction en flux. Pour la rendre possible il nous faut connaître la réponse spectrale instrumentale pour inverser par traitement d'images ce qui c'est produit lors de l'observation. Voici comment l'obtenir cette réponse expérimentalement :

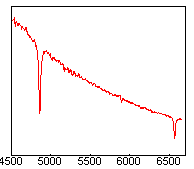
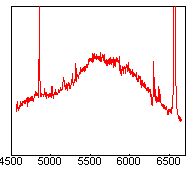
A gauche, vous avez une donnée connue, le spectre observé de Alpha Gémeaux. Ce spectre est le résultat du prétraitement classique vu lors de la seconde session. Rappelez-vous aussi que nous avons divisé le spectre brut par le flat-field normalisé afin de compenser les hétérogénéités de réponse des pixels.

Au centre, on trouve le spectre théorique d'une étoile de même type spectral que Alpha Gémeaux, à savoir le type A1V. On obtient cette donnée dans plusieurs catalogues spectrophotométriques, dont certains sont accessibles depuis le web. Ici nous avons utilisé une base de données compilée par l'astronome A. J. Pickles. Cette base est du reste incluse dans VisualSpec et peut être accédée intéractivement. J'y reviendrais bien sur.

Pour obtenir la réponse spectrale instrumentale il suffit de diviser le spectre observé par son spectre théorique. Le résultat est à droite dans la figure ci-avant. Les irrégularités à petite échelle visibles dans la courbe de réponse ainsi calculée ne sont pas réelles. Elles sont dues principalement à la différence de résolution entre nos spectres et ceux de la base de A. J. Pickles. Pour donner une idée, l'échantillonnage de nos spectres est de 2,9 A/pixel alors que l'échantillonnage dans la base de données employée est de 5 A/pixel. Une technique pour avoir des données comparables consiste à lisser le spectre le plus résolu pour l'amener artificiellement à la résolution du moins résolu avant de procéder à la division. Malgré cela, il va subsister des petites variations accidentelles dans la réponse spectrale, ne serait-ce que par la présence de raies d'origines atmosphérique dans notre spectre.

Les graphiques suivant montrent comment on procède pour retirer ces artefact de petite échelle :

-> lissage ->

A gauche, vous avec la réponse spectrale brute. A droite, nous avons effectué un lissage soigné, qui efface efficacement toutes les petites irrégularités. VisualSpec possède une puissante fonction pour réaliser ce travail. Cette opération est parfaitement légitime car, rappelez-vous que les vraies petites hétérogénéités de réponse ont été retirées lors du prétraitemet grace à la division par le flat-field normalisé.

Alain - J'en déduit que le maximum de sensibilité se situe vers 6000 angstroms ?

Aude - Oui. Cela coïncide en gros avec le pic de sensibilité du CCD, mais rappelez-vous que le rendement spectral du réseau, entre-autre, participe à modeler la courbe de réponse instrumentale.

Une fois la réponse spectrale instrumentale connue, celle-ci peut être utilisée pour corriger tout ou partie des spectres de la nuit. Cependant, en procédant ainsi vous faites l'hypothèse que la transmission spectrale de l'atmosphère ne change pas en cours de nuit, ce qui n'est malheureusement pas toujours le cas. Disons qu'en utilisant une unique courbe de réponse instrumentale pour toute une nuit ou même pour plusieurs nuit, vous allez pouvoir éliminer la plupart des biais d'origine instrumentale. Il subsistera quelques fluctuations non traitées à cause de la variation temporelle de transmission spectrale de l'atmosphère, mais généralement de faibles amplitudes.

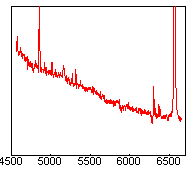
La figure suivante montre comment est effectuée la correction en flux proprement dite. A gauche, vous avez le spectre observé et prétraité de HD45677. Au centre, vous avez la réponse instrumentale. A gauche, après division des deux spectres précédents, vous obtenez la vraie distribution spectrale du flux de l'étoile HD45677. La structure en bosse du spectre non étalonné a disparu. On observe à présent le continuum typique d'une étoile chaude, avec de fortes raies en émission, caractéristiques des étoiles Be.

Alain - Pourquoi avoir choisi l'étoile Alpha Gémeaux ? A t'elle quelque chose de spécial ?

Aude - C'est tout d'abord une étoile brillante, ce qui permet d'obtenir rapidement son spectre avec un bruit négligeable. Elle était haute dans le ciel, mais en même temps loin angulairement de l'étoile HD45677, qui elle était basse sur l'horizon. Soit dit en passant, ce dernier point n'est pas une bonne chose car la transmission différentielle de l'atmosphère entre un objet haut et bas dans le ciel affecte la qualité de l'étalonnage en flux. Surtout cette étoile est de type spectral A. Ce sont des étoiles où, à par la région des raies de l'hydrogène, le continuum est facilement identifiable. L'absence de raies facilite la comparaison entre le spectre observé et le spectre théorique de l'étoile pour extraire la réponse instrumentale. Les étoiles de type O et B sont aussi des bons choix pour la même raison. Les professionnels utilisant de gros télescopes visent même des naines blanches dans lesquelles les raies spectrales sont quasi absentes. Pour bien illustrer ce propos, je vous montre trois spectres théoriques d'étoiles B0V, K0V et M0V respectivement en allant de gauche à droite :

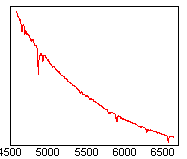
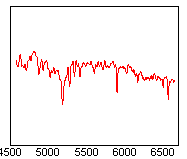
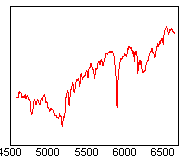
Dans ces exemples, le continuum n'est bien visible que dans l'étoile B. Les autres spectres ont une structure bien trop irrégulière pour que l'on puisse en tirer aisément la réponse instrumentale.

Christian - Quel est le temps de pose pour le spectre de Alpha Gémeaux ?

Aude - C'est une étoile de magnitude V=1,98. Avec la lunette de 106 mm et le petit spectrographe qui nous sert ici, donnant une dispersion de 2,9 A/pixel, le temps de pose est de 12 secondes pour que le signal dans la partie la plus intense du spectre atteigne environ les deux tiers de la dynamique de la caméra Audine. Bien sur, comme il est de règle, je n'ai pas fait qu'un seul spectre de cette étoile, mais 15, afin d'avoir un rapport signal sur bruit très élevé après addition.

Christian - Le rapport signal sur bruit, tu peux préciser ?

Aude - Le rapport signal sur bruit est une quantité très souvent utilisée en imagerie numérique pour quantifier le niveau de bruit. Je vous rappelle que le bruit est l'amplitude de la fluctuation aléatoire autour de la valeur moyenne du signal entre des mesures indépendantes de ce même signal. On a l'habitude de faire le rapport entre le niveau du signal et l'amplitude de la fluctuation afin d'avoir une idée de l'importance relative du bruit. Plus le rapport signal sur bruit est élevé, moins le bruit a une emprise prépondérante dans l'image.

Je vais traiter vite fait bien fait les 15 images de Alpha Gémeaux. Cela vous fera une rapide révision. Les images individuelles ont pour nom AGEM-1, AGEM-2, ... AGEM-15. La tache est simple car nous allons bien sur utiliser les images de référence d'offset, de noir et de flat-field déjà calculées lors de la session 2. Celles-ci sont déjà archivées sur le disque dur sous les noms OFFSET, DARK et FLAT2 respectivement. Affichons la première image de la séquence :

Nous avons sélectionné avec la souris la raie H-beta de l'hydrogène qui apparaît en absorption avec un très bon contraste. Ce sera un bon point commun entre les 15 images pour que Iris puisse faire la registration automatiquement.

Au préalable la commande :

NUMBER AGEM-

nous a appris que nous avions 15 images disponibles.

On ouvre la boite de dialogue de prétraitement des spectres, que l'on remplie de la manière suivante :

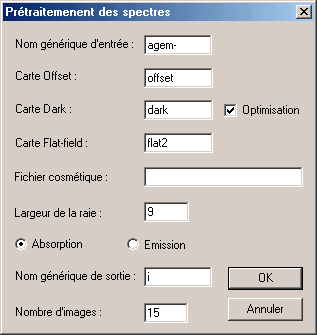
Voici le résultat au terme des calculs :

Le spectre est retourné avec la commande MIRRORY pour amener le rouge à droite, le fond de ciel est retiré intéractivement avec l'aide de la commande L_SKY3 et enfin, on calcule un spectre monodimentionnel en utilisant la commande L_BIN. Tout ceci donne le spectre prétraité de Alpha Gémeaux que voici :

Vous voyez que le traitement n'est pas très long, routinier et que les outils disponibles permettent d'être productif. Vous sauvegardez ce résultat sur le disque sous le nom de votre choix. Pour m'a part je choisis TAGEM_2. L'indice 2 indique un spectre monodimensionel alors que l'indice 1 désignerait un spectre non binné. La lettre T signale un spectre prétraité. Chacun fait comme il veut, le principal étant de s'y retrouver !

A présent lancez le programme VisualSpec et chargez l'image TAGEM_2 via la commande Ouvrir image... du menu Fichier.

En cliquant sur l'icône suivante...

... vous affichez le profil spectral sous la forme d'une courbe :

Christian - C'est un peu comme la commande L_PLOT que nous avons utilisé avec Iris lors de la session précédente.

Aude - Pas tout à fait. La fonction de VisualSpec que nous avons utilisé est en quelque sorte la combinaison de la commande L_BIN et L_PLOT. Cela signifie que VisualSpec accepte des spectres bidimentionnels et est capable de faire un binning intelligent et optimisé pour extraire un profil spectral. Simplement, j'ai fait ici ingurgiter à VisualSpec une image spectrale qui a déjà subit le binning. Vous avez la possibilité de faire cette dernière opération dans l'un ou l'autre logiciel.

Il nous faut à présent identifier quelques raies spectrales afin de réaliser la calibration en longueur d'onde. C'est une étape assez délicate lorsque l'on débute en spectrographie. Que vous inspire le spectre de Alpha Gémeaux à ce propos ?

Raymond - Il me semble avoir compris que la grosse raie à droite est la raie H-alpha de l'hydrogène et la grosse raie à gauche est la raie H-beta du même atome d'hydrogène.

Aude - Oui c'est bien cela. Ce sont les raies les plus marquantes dans une étoile de type spectral A ou B lorsque le domaine spectral couvert va du rouge profond au bleu-vert. Dans des étoiles plus froides, les raies de l'hydrogène diminuent d'intensité alors que le nombre de raies en provenance d'autres éléments chimiques augmente fortement, rendant le travail d'identification problématique lorsque l'oeil n'est pas exercé. Moralité : viser des étoiles de type A ou B pour vous faire la main lors de vos premiers pas en spectrographie ou lorsque, comme ici, nous devons réaliser la premier étalonnage spectral d'un nouveau spectrographe.

Le fait d'avoir identifié deux raies de manière sure dans le spectre nous permet déjà de réaliser un étalonnage approximatif du spectre en faisant l'hypothèse que la relation entre le rang d'un pixel dans le profil et la longueur d'onde associée est linéaire. Dans ce cas il est possible d'écrire :

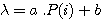
avec l la longueur d'onde, P(i) la position dans le spectre en pixel et (a, b) deux paramètres que l'on calcule aisément à partir de la position en pixel dans le spectre des deux raies et de leurs longueurs d'ondes.

Alain - Il me semble voir d'autres raies moins intenses. Tu peux nous dire de quoi il s'agit ?

Aude - Dans le profil spectral suivant de notre étoile Alpha Gémeaux j'ai identifié quelques raies et leur longueur d'onde en angstroms avec une précision suffisante lorsque l'on veut étalonner un spectre obtenu avec un spectromètre ayant un pouvoir de résolution inférieur à 1000, ce qui est le cas ici. Le symbole Mg désigne le magnésium et le symbole Na le sodium. La raie O2 est en fait une bande comprenant de nombreuses raies produites par l'oxygène atomique de l'atmosphère terrestre. On les appelle des raies telluriques à cause de cela.

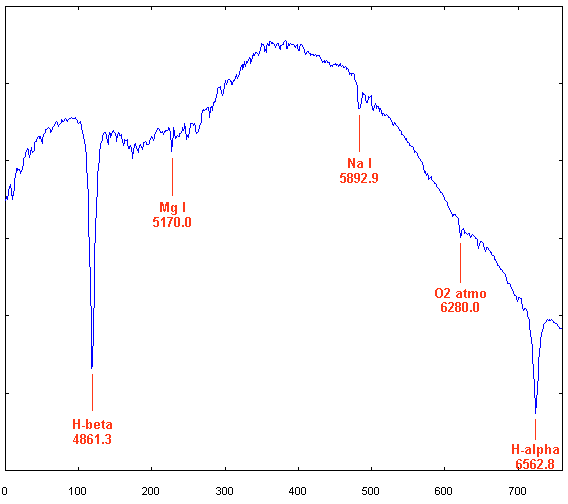
Le fait de disposer d'un nombre de raies plus grand que deux pour effectuer l'étalonnage spectral permet de calculer une loi de dispersion non linéaire, qui donne généralement une précision supérieure.

Alain - Un modèle de dispersion linéaire n'est donc pas assez précis.

Aude - Pas toujours en effet. C'est le cas ici car l'étendue spectrale est grande et la courte focale de l'optique utilisée, un objectif photographique de 50 mm, produit une certaine distorsion dans le spectre. En outre, l'examen de la formule du réseau que je vous ai décrite lors de la deuxième session montre que la dispersion ne peut être assimilée raisonnablement à une loi linéaire sur un grand intervalle spectral. Donc la réalité est plus complexe.

La relation entre la position en pixel dans le spectre et la longueur d'onde s'obtient alors en ajustant un polynôme d'un certain degré en utilisant toutes les raies connues dans le spectre. Dans notre exemple, l'expérience montre qu'il suffit d'un polynôme du deuxième ordre pour établir un étalonnage en longueur d'onde de tous les pixels à un angstroms près, ce qui est déjà très bien compte tenu de la classe du spectrographe. Je rappelle en effet ici que la résolution spectrale effective est de 7 ou 8 angstroms. Nous devons donc calculer les paramètres (a, b, c) d'une équation du type :

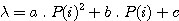
Alain - C'est l'équation d'une parabole. Pourquoi ne pas utiliser des ordres plus élevés.

Aude - C'est bien une loi parabolique en effet. Il est dangereux d'utiliser un polynôme de degrés trois par exemple si on n'a pas à notre disposition 7 à 8 raies très bien réparties dans le spectre. D'une manière générale, plus le polynôme a un degré élevé, plus il suit de près les points de mesure qu'on lui fournit... même s'il y a une erreur importante de mesure. C'est parfois problématique, en particulier lorsqu'il faut extrapoler la courbe de dispersion en dehors de la zone définie par le jeu de raies spectrales étalon. Sur ce plan, une loi linéaire ou une loi parabolique est plus tolérante vis à vis des erreurs.

Christian - Comment fait on l'étalonnage spectral en pratique avec VisualSpec ?

Aude - VisualSpec dispose de plusieurs outils pour cela. Nous allons utiliser celui qui ajuste un polynôme par la technique des moindres carré, un méthode robuste et très classique pour résoudre ce type de problème.

Vous lancer la commande Calibration non-linéaire du menu Spectrométrie. A partir de ce moment vous devez sélectionner avec la souris les raies de votre choix dans le spectre. VisualSpec calcule pour vous la position de ces raies à une fraction de pixel près. Vous devez par ailleurs fournir la longueur d'onde associée aux raies sélectionnées. Au final, un tableau est créée petit à petit avec dans une colonne la longueur d'onde et dans une autre colonne la position de la raie dans le profil spectral :

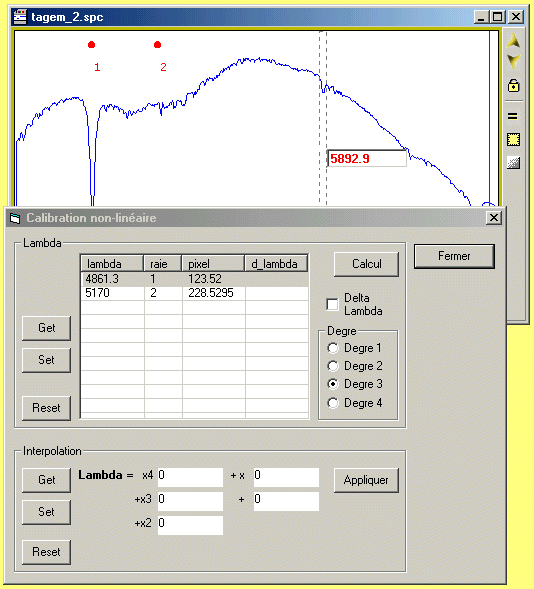
Au terme de la sélection de raies, vous choisissez le degré du polynôme, puis vous cliquez sur le bouton Calcul pour déterminer les paramètres du polynômes, qui s'affichent en bas de la fenêtre :

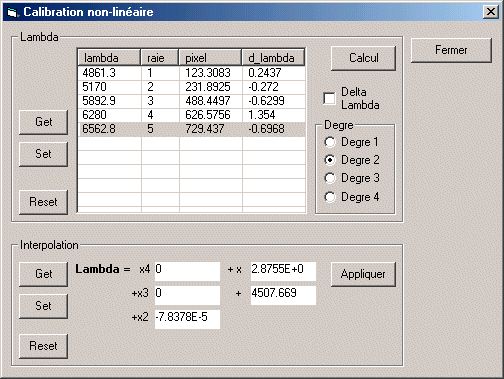
La relation entre la position en pixel et la longueur d'onde dans notre exemple est la suivante :

Les écarts en longueur d'onde entre les valeurs calculées avec ce polynôme et les longueurs d'ondes fournies au logiciel apparaissent dans la dernière colonne du tableau (d_lambda).

Enfin, en cliquant sur la bouton Appliquer, vous convertissez l'axe des abscisses gradué en pixel en un axe gradué en longueur d'onde.

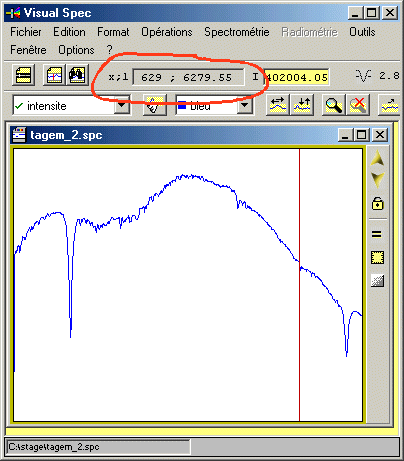
Dorénavant, une modification importante c'est produite dans la barre d'outils de VisualSpec : lorsque vous déplacez la souris dans l'image, le programme affiche directement sa position en pixel, mais aussi en longueur d'onde. Dans la figure suivante, au pixel de rang 629 est associé la longueur d'onde de 6279,55 Å.

Alain - En se limitant à l'ordre 1 qu'elle aurait été l'erreur en calibration spectrale ?

Aude - L'équation trouvé dans ce cas est :

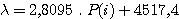
L'erreur de calibration atteint jusqu'à ±5 Å sur la majorité du spectre. La loi de dispersion s'écarte signification d'une droite, et le choix d'une loi parabolique se justifie ici pleinement.

L'étalonnage en longueur d'onde du spectre de Alpha Gémeaux est à présent terminé. Vous pouvez sauvegarder le profil spectral en utilisant la commande Enregistrer sous... du menu fichier. Le résultat de la calibration est sauvegardé en même temps. Lors du prochain chargement de ce spectre il s'affichera donc automatiquement avec des graduations en longueur d'onde.

Retour à la page d'accueil du stage Page précédente Page suivante