Leçon 10 : Le calcul d'un super flat-field

Il existe des circonstances où il est difficile de réaliser des images flat-field dans les conditions normales, c'est à dire au crépuscule. Un palliatif possible consiste à acquérir les images flat-field en pointant le télescope vers un écran (intérieur d'une coupole par exemple éclairée par un projecteur) ou mieux encore en disposant à l'entrée du télescope un diffuseur (plusieurs épaisseurs de papier calque par exemple) qui est éclairé par une lampe présentant une température de couleur assez élevée (un coup de flash d'appareil photographique est souvent une solution appropriée). Ces solutions de secours ne fonctionnent malheureusement pas toujours, notamment lorsqu'il faut corriger les petites ombres issues de poussières situées non loin de la surface sensible.

Une autre possibilité pour déterminer le flat-field est de l'extraire des images de la nuit même. Le résultat est alors généralement excellent puisque pratiquement aucun biais ne vient s'interposer entre les images scientifiques et les images d'étalonnage. On nomme pour cela ce type de flat-field un super flat-field. L'inconvenient est que le niveau moyen du flat-field est bas puisque les images sont réalisées de nuit. Parfois, le site d'observation est pollué par de la lumière parasite et si celle-ci devient un atout pour réaliser un super flat-field. Il faut souligner enfin qu'un super flat-field ayant un niveau moyen du même ordre de grandeur que le niveau du fond de ciel des images à traiter apporte peu de problèmes si l'objectif est d'observer des objets très faibles, sortant à peine du fond de l'image.

Télechargez le fichier LECON10.ZIP qui contient les images servant d'exemple dans cette leçon. Décomprimez ce fichier dans votre répertoire de travail.

La séquence F1.PIC à F11.PIC est caractéristiques d'images réalisées spécialement pour synthétiser un super flat-field : le temps de pose est relativement long (300 secondes) afin de faire "monter" le fond de ciel et surtout, entre chaque image le télescope a été déplacé aléatoirement (de quelques dizaines de pixels au moins et parfois de champs complets). Le nombre d'image est relativement grand, ce qui est aussi un gage de succés. Les figures ci-après montrent les deux premières images de la séquence (notez la position des étoiles par rapport aux poussières  qui apparaissent sous la forme de grandes auréoles noires ) :

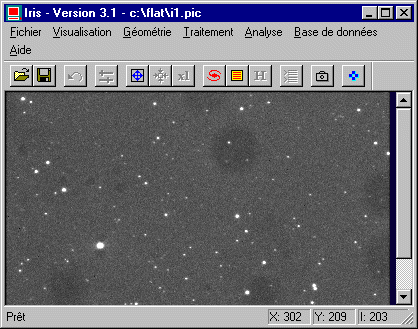
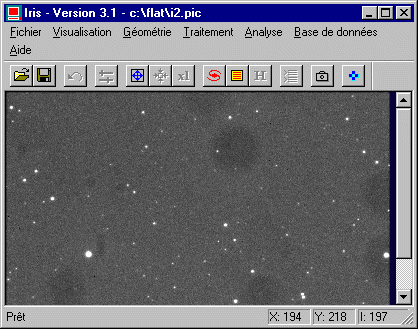
Les 11 images de la série F1....F11 sont brutes, c'est à dire qu'il faut leur retiré le signal d'offset et le signal d'obscurité du CCD. L'image d'offset a pour nom OFFSET.PIC (notez que le signal d'offset a été assimilé à un niveau constant, ce qui est assez souvent légitime). L'image du signal thermique a pour nom DARK.PIC. Il s'agit de la médiane d'un grand nombre d'images posées 300 secondes dans l'obscurité totale. Il faut souligner que le signal d'offset a déjà été retiré de l'image DARK.PIC. Cette dernière image est bien représentative du signal d'obscurité seul.

Commencez par prétraiter les 11 images.

Tout d'abord le retrait du signal d'offset (commande Soustraire à une séquence... du menu Traitement) :

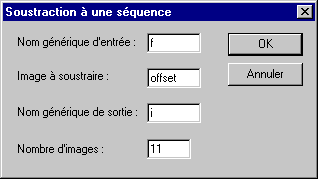
Cette opération créée la nouvelle séquence i1...I11.PIC.

Il faut ensuite retirer le signal thermique. Avant la soustraction proprement dite il est nécessaire de calculer le coefficient multiplicatif à appliquer à l'image DARK.PIC afin que le signal thermique soit elliminé au mieux dans les images I1...I11.PIC. Il faut utiliser pour cela la technique de l'optimisation du noir. Définissez une zone rectangulaire dans la première image de la séquence (I1.PIC) qui n'englobe pas d'étoiles brillantes, puis activez le menu contextuel (click droit avec la souris) et lancez la commande Optimisation du noir...

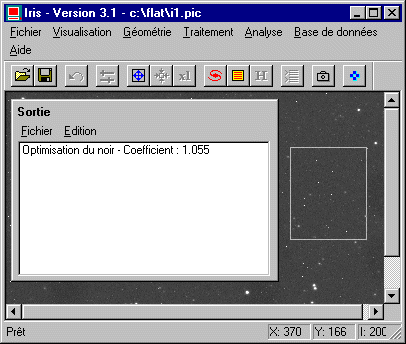
IRIS retourne la valeur du coefficient optimal, ici 1.055, une valeur proche de 1 car les noirs et les flats ont été fait avec le même temps de pose et à peut de temps d'intervalle. Multiplions l'image DARK.PIC par ce coefficient et sauvegardons le résultat sous le nom N.PIC (commande Multiplication...). Chargez DARK.PIC en mémoire, puis faire :

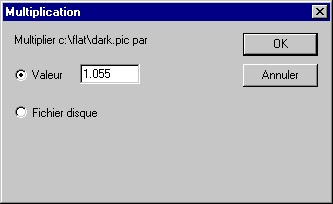
Sauvons le résultat sous le nom N.PIC puis retirons cette dernière image à la séquence I1...I11.PIC :

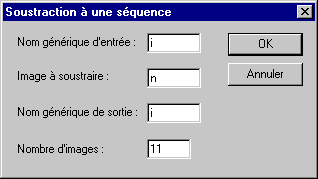
Remarquez que la séquence de sortie a écrasé la séquence d'entrée dans c'est exemple.

L'opération finale pour synthétiser le flat-field consiste à calculer la valeur médiane de la pile d'images I1...I11.PIC. En effet, comme les étoiles ne se trouvent pas au même endroit d'une image à l'autre, l'analyse statistique permettra d'extraire l'information commune aux 11 images, c'est à dire le fond de ciel épuré de tout objet. Un petit rappel : supposons que l'intensité d'un même pixel dans 5 images soit :

1241 560 1300 1310 1292

Cette distribution d'intensité est triée suivant l'ordre croissant :

560 1241 1292 1300 1310

La valeur médiane est alors 1292. Cette intensité est bien plus proche de la réalité que celle que l'on aurait obtenue en faisant la moyenne arithmétique des 5 valeurs (soit 1141) car le pixel aberrant d'intensité 560 a été éliminé d'office après l'opération de trie.

Une sage précaution avant d'effectuer la somme médiane est de toujours s'assurer que le niveau du fond de ciel n'a pas varié d'un image à l'autre. Pour en être sur, le fond de ciel des 11 images est forcé d'autorité à 200 (200 est en gros le niveau du fond de ciel dans les images de la séquence I). Utilisez pour cela la commande Normalisation de l'offset d'une séquence... :

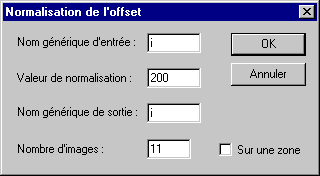
Reste à présent le calcul de la médiane :

Voici le résultat, que l'on sauve sous le nom FLAT.PIC :

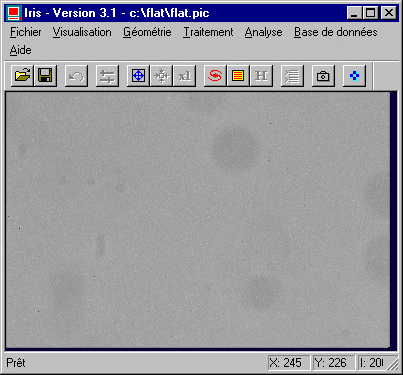
Remarquez que les étoiles ont pratiquement disparues, en revanche les poussières sont bien visibles.

A titre de contrôle vous pouvez diviser l'image I1.PIC (par exemple) par le super flat-field et ainsi vérifier que tout se passe bien :

LOAD I1
DIV FLAT 200

A remarquer pour finir cette leçon que la procédure que nous avons décrite pour déterminer le super flat-field, ne s'éloigne pas fondamentalement de ce qu'il faut faire sur des images flat-field acquises au crépuscule car elles contiennent assez fréquemment des étoiles, en moins grand nombre que dans l'exemple ci-dessus, mais tout de même gênantes. Le compositage médian bien appliqué est donc un outil très précieux.

Les opérations de cette leçon sous la forme de lignes de commandes seraient par
exemple :

LOAD DARK
MULT 1.055
ADD OFFSET
SAVE N
SUB2 F N I 0 11
NOFFSET2 I I 200 11
SMEDIAN 11
SAVE FLAT
LOAD I1
DIV FLAT 200
LOAD I2
DIV FLAT 200
...