Leçon 15 : La photométrie d'un objet mobile

Nous allons étudier l'outil Photométrie Automatique de IRIS. Celui-ci permet de mesurer automatiquement l'éclat d'étoiles dans une séquence d'images. Il est possible de mesurer simultanément jusqu'à 5 objets distribués dans les images.

L'application première de ce type de fonction est la mesure de la variation de la magnitude d'un objet en fonction du temps. L'objet sera par exemple une étoile variable ou encore un astéroïde (dans ce dernier cas la variation d'éclat est produite par la rotation sur lui-même d'un corps ne présentant pas de symétrie de révolution). Parmi les 5 étoiles sélectionnable, la première sera l'objet variable, ou soupçonné de l'être. Les 4 autres étoiles sont des étoiles dites de comparaison, dont l'éclat est réputé stable. Le principe d'analyse est différentiel : on compare l'éclat de l'objet variable à celui des étoiles fixes. Le résultat de l'analyse est la différence d'éclat entre l'objet étudié et une ou plusieurs étoiles de comparaison, et on parle de technique de photométrie différentielle. Le fait de disposer de plusieurs étoiles permet de réduire l'erreur de mesure par moyennage ou encore, de détecter la présence d'un objet parasite variable dans les étoiles de comparaison.

Le cas de la mesure d'un astéroïde est particulier car l'objet est mobile parmi le champ d'étoiles en arrière plan. L'outil d'analyse doit dont tenir compte de ce mouvement afin d'être sur de mesurer toujours le même objet en fonction du temps.

Pour illustrer le propos nous allons analyser une séquence de 132 images de l'astéroïde 14-SIWA. Ces images ont été acquises par Jean Montanné avec un LX200 de 8 pouces depuis une terrasse du Pic du Midi le 07/08/2000.

Vous pouvez télécharger les 3 premières images de cette séquence (fichier LECON15.ZIP de 1.0 Mo). Attention, les images sont au format FITS.

La focale du télescope est de 1016 mm et la taille des pixels est de 9 x 9 microns (caméra Audine). Le temps de pose est de 60 secondes. Le centre du champ est aux coordonnées AD=21H23m, DEC=-18°23'.

La durée d'acquision d'une telle séquence peut atteindre plusieurs heures et bien sur les problèmes de dérive du télescope peuvent produire un bougé significatif d'une image à l'autre en l'absence d'autoguidage. La fonction d'analyse photométrique de IRIS peut réaliser le recentrage des images pour vous automatiquement, mais si vous débutez, préférez réaliser l'opération en dehors de cette fonction. C'est aussi un excellent exercice de révision ! Pour ce faire utiliser la commande Registration des images planétaires... du menu Traitement (ou la commande REGISTER depuis la ligne de commande). Généralement, il est suffisant d'effectuer la registration avec une seule étoile. En cas de doute, relire la leçon 7.

Une fois la registration effectuée, une bonne idée est d'examiner la séquence en utilisant l'outil d'animation (commande Animation... du menu Visualisation) :

L'astéroïde est visible en bas de l'image. Son déplacement est très sensible et il faut en tenir compte, nous l'avons dit, pour effectuer correctement la photométrie.

Prendre une image en début de séquence et une autre en fin de séquence (respectivement les images à gauche et au centre ci-après). Noter les jours Julien de l'instant d'acquisition. Cette information est retournée par la commande INFO que l'on tape depuis la console de commande. Par exemple faire :

LOAD SIWA1
INFO
LOAD SIWA132
INFO

 On trouve les dates respectives suivantes :

- pour SIWA1 : JD = 2451764.3889
- pour SIWA132 : JD = 2451764.5758

soit un écart de temps de 2451764.5758 - 2451764.3889 = 0.1869 jour.

Vous devez ensuite déterminer le déplacement en pixels de l'astéroide suivant les axes X et Y entre ces deux images extrêmes. Un moyen rapide consiste à additionner les deux images (le résultat est à droite dans la figure ci-dessus), puis vous lancez la commande DIST depuis la ligne de commande. IRIS attend alors de vous deux clicks : l'un sur la première image de l'astéroïde et l'autre dans la seconde (la position précise du curseur de souris n'est pas très critique). Après le second click, IRIS retourne le déplacement en X et Y entre les deux prises de vues. On trouve :

DX = -71.377 pixels
DY = -34.993 pixels

Le déplacement journalier de l'astéroïdes en pixels est donc :

VX = -71.377 / 0.1869 = -381.900 pixels/jour
VY = -34.993 / 0.1869 = -187.228 pixels/jour

Sélectionnez les objets suivant, comme lors de la leçon 13, en utilisant la commande Sélection d'objets du menu Traitement (l'astéroïde est noté 1) :

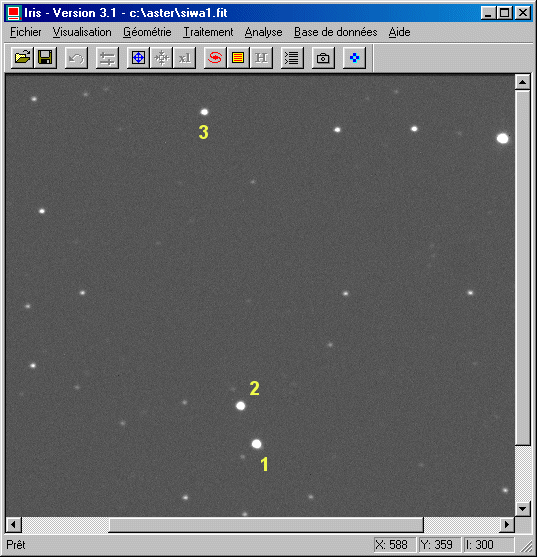
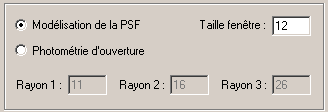
A présent remplissez les champs de la boite de dialogue de Photométrie automatique... (menu Traitement) de la manière suivante :

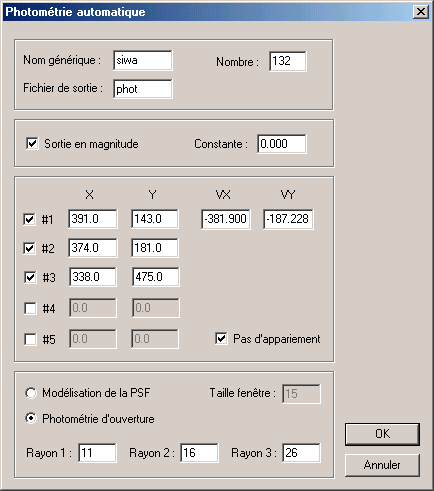
Nous avons choisi d'utiliser la technique de la photométrie d'ouverture (voir la leçon 12). Le type d'algorithme utilisé est celui qui calcule un fond de ciel median. Les paramètres peuvent être choisis par essais successifs (voir plus loin). Remarquez que les champs VX et VY ont été rempli avec la vitesse journalière de l'astéroïde. L'option Pas d'appariement est aussi sélectionnée : cela signifie que IRIS ne va pas chercher àsuperposer les images lors du traitement (inutile puisque la registration est déjà effectuée). Dans le cas contraire, IRIS effectuerait au fur et à mesure de l'analyse la registration de manière automatique.

Cliquez sur OK. Vous pouvez apercevoir dans la fenêtre de sortie le résultat du traitement en temps réel. Au terme du traitement, IRIS produit un certain nombre de fichiers dans le répertoire de travail.

Le fichier VERIF.DAT contient des valeurs entières qui représentent la différence en magnitude entre la première étoile sélectionnée et la magnitude calculée en faisant la somme des intensités des étoiles de comparaison. L'objet de ce fichier est de permettre un contrôle rapide du résultat depuis la fenêtre Graphe (menu Visualisation), mais ne doit pas être utilisé pour une exploitation scientifique :

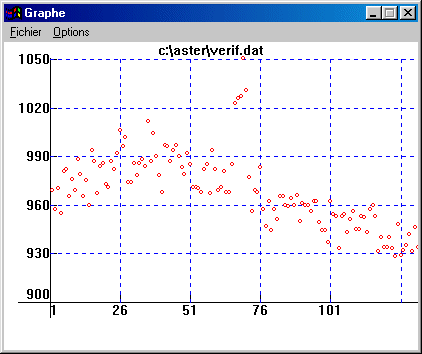
L'astéroïde montre une lente variation d'éclat provoquée par la rotation sur lui même. Les points déviants vers le milieu de l'observation sont causés par une étoile du champ qui pollue la mesure.

Le fichier principal de sortie a dans notre exemple pour nom PHOT.LST (c'est le nom que vous avez fourni dans la boite de dialogue). Voici son contenu typique :

2451765.41241   -9.906    -9.570    -9.603   
2451765.41323   -9.992    -9.535    -9.694   
2451765.41404   -9.970    -9.632    -9.700   
2451765.41487   -10.053   -9.553    -9.711   
2451765.41568   -10.017   -9.574    -9.747   
2451765.41650   -10.008   -9.611    -9.628   
2451765.41734   -9.929    -9.535    -9.740   
2451765.41816   -9.937    -9.501    -9.629   
2451765.41898   -9.996    -9.556    -9.646   
2451765.41981   -10.019   -9.569    -9.725   
2451765.42065   -9.979    -9.628    -9.750   
2451765.42147   -9.972    -9.584    -9.588   
2451765.42231   -9.869    -9.460    -9.447   
2451765.42314   -9.869    -9.452    -9.470   
2451765.42396   -9.770    -9.388    -9.444  

La première colonne contient le jour Julien (une ligne par image), puis les colonnes suivantes sont associées aux étoiles sélectionnées. Dans cet exemple les magnitudes sont instrumentales (ce qui explique les valeurs négatives). Vous pouvez avoir des magnitudes plus proches de la réalité en remplissant le champ Constante (des magnitudes) de la boite de dialogue de Photométrie automatique.

Le fichier DELTA.DAT est aussi, dont voici un extrait :

1     -0.433339
2     -0.378491
3     -0.449788
4     -0.334538
5     -0.399466
6     -0.363487
7     -0.465965
8     -0.382446
9     -0.358777
10    -0.382895

DELTA.DAT contient la différence en magnitude (ou en flux si vous ne cochez pas l'option Sortie en magnitude) entre la première colonne (en principe l'objet variable) et la magnitude calculée en faisant la somme des intensités des étoiles de comparaison. C'est en traçant le graphe de ce fichier que vous pourrez éventuellement détecter la variation d'éclat de votre objet.

La fichier DELTA2.DAT est très similaire au fichier DELTA.DAT à ceci près qu'à la place du numéro d'ordre dans la première colonne on trouve le jour Julien :

2451765.412407 -0.433339
2451765.413229 -0.378491
2451765.414039 -0.449788
2451765.414873 -0.334538
2451765.415683 -0.399466
2451765.416505 -0.363487
2451765.417338 -0.465965
2451765.418160 -0.382446

Pour vérifier la consistance de votre analyse il ne faut pas hésiter à mesurer l'éclat des étoiles de comparaison entre-elles. Si la première étoile sélectionnée est une étoile non variable, vous pouvez relever en particulier le niveau de précision de la réduction photométrique au travers de l'information Ecart-type retournée par IRIS dans la fenêtre de sortie à la fin du traitement. Il s'agit de la déviation par rapport à la moyenne des différences de magnitude de l'objet de la première colonne et de la magnitude des objets de comparaison (somme de leur intensité). Plus l'écart-type à une petite valeur, meilleure est l'estimation des magnitudes. Voici un exemple :

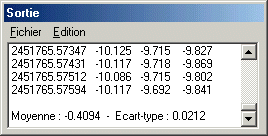
Une bonne habitude à prendre est de tester la précision photométrique (écart-type) en ajustant certain paramètres, et notamment en matière de photométrie d'ouverture, la taille des différents cercles (en particulier le cercle intérieur). Attention aussi au sous-échantillonnage des images stellaires, qui est l'un des facteurs majeur affectant la précision. Ne pas hésiter à utiliser la commande ASCALE (voir la discussion lors de la leçon 12), qui apportera souvent un gain significatif lorsque les images sont acquises avec un petit instrument ou avec un fort facteur de binning. La commande ASCALE2 permet de re-échantillonner de manière optimale une séquence pour la photométrie d'ouverture. Par exemple :

ASCALE2 SIWA I 132

Dans l'exemple ci-après on a tracé la valeur de l'écart type en fonction du rayon intérieur en photométrie d'ouverture. On note un minimum relativement bien marqué et on utilisera le rayon correspondant pour étudier une étoile variable par exemple. Le FWHM typique des étoiles (largeur à mi-hauteur) dans cet exemple est de 2.3 pixels (commande PSF du menu contextuel).

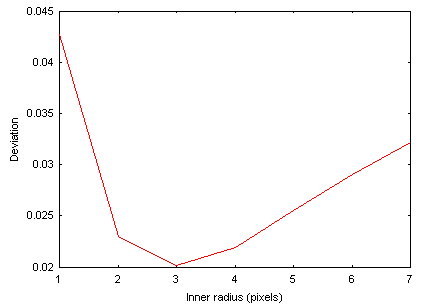
La photométrie automatique peut être réalisée par modélisation de la PSF (PSF = fonction d'étalement de l'étoile) :

Dans ce cas vous pouvez préciser la taille en pixel du carré à l'intérieur duquel l'ajustement de l'étoile est effectué. Tout comme pour la dimension des cercles en photométrie d'ouverture, vous devez ajuster soigneusement ce paramètre en traçant l'écart type en fonction de sa valeur (mesurer alors des étoiles d'éclat supposé constant). D'une manière générale la taille de la fenêtre vaut 4 à 5 fois la valeur du FWHM (largeur à mi-hauteur des étoiles). Si la dimension est trop grande, le logiciel va essayer d'ajuster le bruit du fond de ciel, ce qui n'est pas bon. Si la taille est trop petite, la modélisation mathématique ne sera que fragmentaire, ce qui n'est pas bon non plus. L'exemple ci-après montre l'erreur photométrique (à 1 sigma) en fonction de la taille de la fenêtre d'ajustement (le FWHM des étoiles est ici de 2.3 pixels).

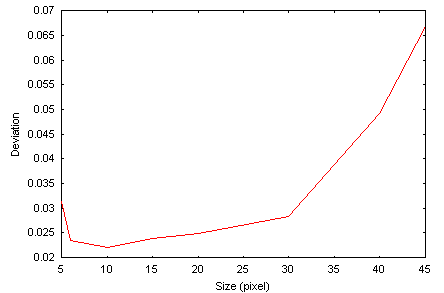
Généralement, on préférera la méthode de l'ajustement de la PSF dans le cas de l'étude d'un objet mobile ou lorsque la densité d'étoiles est importante, car la taille de la zone d'analyse est plus petite que ce qui est nécessaire en photométrie d'ouverture. Cependant, contrairement à une idée reçue assez fortement encrée, la précision ultime en photométrie est atteinte en exploitant de simples cercles d'ouvertures. La conjonction d'un calcul soigné du fond de ciel (valeur médiane avec réjection par exemple), d'un échantillonnage optimal de l'image (commandes ASCALE et ASCALE2, voir aussi Mighell, K. J. & Rich, R. M. 1995, AJ, 110, 1649) et d'un ajustement optimal de la taille des cercles d'ouverture sur un critère d'erreur quadratique, permet bien souvent à la photométrie d'ouverture de dépasser la technique d'ajustement de la PSF. Le résultat de la photométrie d'ouverture est en outre moins sensible aux déformations des étoiles provoquées par des erreur de suivi du télescope, ce qui n'est pas un mince avantage avec les instruments amateurs.

Le graphe ci-après montre l'erreur photométrique pour différents méthodes de mesures sur une séquence de 200 images (FWHM des étoiles de 2.3 pixels). On a choisit de comparer l'éclat relatif d'étoiles de comparaison (donc stables photométriquement). Ces courbes sont directement issues des fichiers DELTA.DAT produits par IRIS.

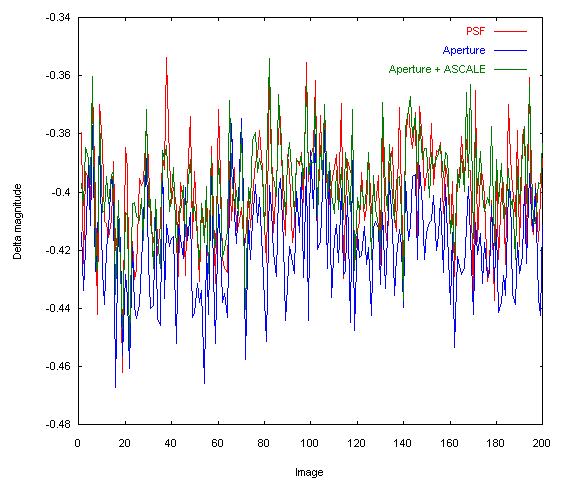
Voici le bruit en magnitude (à 1 sigma) relevé dans ces différentes distributions :

Ajustement de la PSF : 0.0187
Photométrie d'ouverture simple : 0.0184
Photométrie d'ouverture avec une grille de pixels deux fois plus fine (APHOT2) : 0.0164

Il faut remarquer que la taille du cercle d'ouverture optimal trouvé par essais successifs est très proche en photométrie d'ouverture simple et en photométrie d'ouverture avec re-échantillonnage (ici une valeur de 5 pixels de rayon). C'est cette propriété qui confère le gain en précision radiométrique dans le cas du re-échantillonnage car le cercle est ici plus petit en relatif par rapport à la taille des étoiles, et donc la contribution du bruit est moins prédominant.

Noter que pour beaucoup, le résidu de fluctuation est induit par la scintillation atmosphérique. Seule des techniques comme la moyenne des mesures contiguës (moyenne glissante) permettent alors d'accroître la résolution photométrique, mais ce, au détriment de la résolution temporelle.