Leçon 19 : La cartographie planétaire (partie 1)
Cette leçon aborde le problème de la construction de vue cartographique des images planétaires à partir de leur observation télescopique.
Au télescope, une planète apparaît sous la forme d'un disque qui est en fait la projection dans un plan du globe planétaire. Cette projection produit des distortions : un détail proche du limbe apparaît plus compressé que s'il était présent au centre du disque. L'effet de perspective donne du relief à l'image, mais en même temps, l'interprétation et la mesure des détails présents sur le globe planétaires en souffre. Il est ainsi difficile à partir d'une vue télescopique d'analyser l'évolution d'un détail en fonction du temps tellement l'aspect apparent est dépendant de la position de ce détail sur le disque. La vue télescopique ne donne en outre qu'une vue partielle de l'ensemble de la topologie de la planète, puisque au mieux, il n'est possible à un même moment de ne voir qu'un demi hémisphère.
L'idée de la cartographie est de présenter l'image planétaires en utilisant de nouvelles projections qui ont des propriétés géométriques ou visuelles attractives. Par exemple on pourra choisir de représenter la planète de telle manière qu'une distance mesurée sur la carte ai la même échelle suivant un axe vertical ou horizontal quel que soit l'endroit de la planète représenté. Il est possible aussi de choisir des projections de manière à ce que l'on ai une vision globale, sur 360°, de l'ensemble de la planète en une seule fois, ou encore des projections qui favorisent l'étude des pôles.
La science de la cartographie est nécessairement inexacte du fait que des déformations locales où globales dans la carte sont inévitables. Le choix de la projection cartographique est généralement basé sur des compromis entre différentes propriétés.
Les opérations cartographiques sont possibles avec Iris en utilisant la seule commande MAP, ainsi que quelques autres fonctions utilitaires. MAP est une commande puissante et extrêmement riche en possibilités. Pour débroussailler le terrain rien ne vaut un exemple bien concret.
Nous allons essayer de construire un planisphère complet de la planète Jupiter à partir de 5 images réalisées les 16 et 17 août 1987 avec le télescope de 1 mètre du Pic du Midi. Ces images, obtenues avec une caméra expérimentale reposant sur un CCD TH7852A, sont historique : se sont pratiquement les premières images planétaires réalisées avec une matrice CCD sur ce prestigieux télescope. Un époque héroïque qui amorçait un cycle d'observations planétaires remarquables, qui se perpétue encore aujourd'hui.
Pour télécharger les 5 images de Jupiter, cliquez ici (fichier JUPI.ZIP - taille de 150 Ko).
Voici la première image brute de la série qui date du 16/08/1987 à 3H18 TU dont le contraste été rehaussé avec un léger filtrage du type masque flou (commande UNSHARP) :
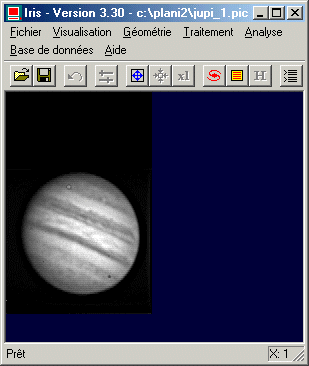
Le CCD utilisé ne possède pas des pixels carré ce qui produit un allongement d'environ 6.67% suivant l'axe vertical par rapport à l'axe horizontal (la taille des pixels est de 28x30 microns). Il est extrêmement important en matière de cartographie que les deux axes du CCD soient homothétiques. Pour ce faire l'image doit être légèrement comprimé suivant l'axe vertical avec l'aide de la commande SCALE :
SCALE 2 1 0.9333
Le premier paramètre (valeur 2) défini le type d'interpolation, ici une interpolation bilinéaire. Les second et troisième paramètres définissent le facteur d'échelle respectivement suivant les axes X et Y.
Voici le résultat :

Dans un objectif de simplification, il est important avec la présente version de Iris d'orienter le disque de la planète de telle manière que l'axe de rotation soit vertical et que le nord soit en haut du disque. La commande qui permet de réaliser cette opération est la commande ROT (vous pouvez aussi utiliser la commande Rotation... depuis le menu Géométrie). Les deux premiers paramètre de la commande ROT sont les coordonnées du centre de rotation, qu'il faut ici choisir comme étant le centre approximatif du disque planétaire. Dans le cas présent on trouve facilement en utilisant le curseur de la souris les coordonnées (78, 75). Le troisième paramètre de la commande ROT est l'angle de rotation de manière à amener l'axe de la planète vertical. Il y a plusieurs manière de déterminer c'est angle. Si l'axe horizontal des pixels de la matrice CCD est parfaitement orienté suivant l'axe Est-Ouest céleste, l'angle est alors donnée de manière rigoureuse dans les éphémérides au travers d'un paramètre appelé Angle de position (ou angle géocentrique de position du pole de rotation nord). Iris possède un petit module de calcul d'éphémérides qui fourni, entre-autre, ce paramètre pour les planètes Jupiter et Mars. Dans le cas présent invoquez la commande Ephémérides de Jupiter... depuis le menu Analyse et contentez-vous d'entrer la date de l'observation, puis enfin de cliquer sur le bouton Calcul :
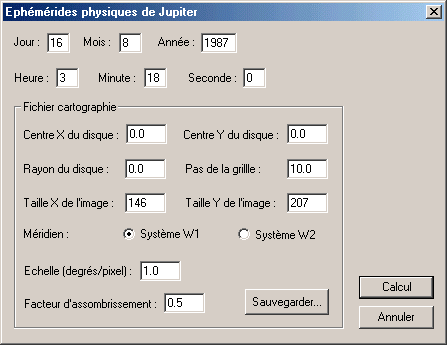
Iris fournie alors dans le fenêtre de sortie de résultats quelques paramètres physiques de Jupiter au moment de l'observation et notamment l'angle de position, qui vaut ici 338.1° (c'est angle est mesuré à partir du nord céleste en allant vers l'est, il est de 0° au nord, de 90° à l'est, de 180° au sud et de 270° à l'ouest).
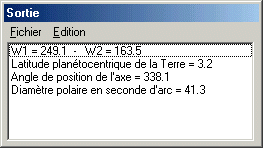
Mais c'est angle n'est pas ici directement applicable pour définir l'angle de rotation du disque car malheureusement l'axe horizontal du CCD est orienté nord-sud. En tenant compte de ce fait, on trouve en fin de compte que l'angle à appliquer est de 201.9°.
Un technique plus expéditive est d'estimer approximativement à l'oeil l'angle d'inclinaison de l'axe de rotation de la planète, de tourner le disque avec cette information et d'appliquer au besoin des corrections par approches successives.
Astuce : lorsque vous définissez une ligne de coupe dans l'image (commande Coupe du menu Visualisation), Iris retourne l'angle de cette ligne de coupe, ce qui peut être d'une bonne aide pour la première estimation de l'orientation de l'axe de rotation de la planète).
Par itération on trouve que le bon angle est de 201°. On tapera alors la commande :
ROT 78 75 201
Voici le résultat de l'opération que l'on sauvegarde (sous le nom JUP1 par exemple) :

Bien entendu dans le cas d'une série, l'angle de position est en principe identique pour toute les images et ne doit donc être déterminé qu'une seule fois.
A ce stade nous allons définir les paramètres cartographique proprement dit de notre image.
Vous devez tout d'abord déterminer le centre précis du disque de la planète ainsi que son rayon en pixel. Pour ce faire, la commande idéale est CIRCLE. Définissez un rectangle en glissant avec la souris (bouton gauche enfoncé) englobant l'intégralité du disque de Jupiter, puis entrez la commande :
CIRCLE 400
Le paramètre (400) est un seuil qui est choisi arbitrairement de telle manière que l'essentiel du disque de Jupiter ai une intensité supérieure à ce seuil :
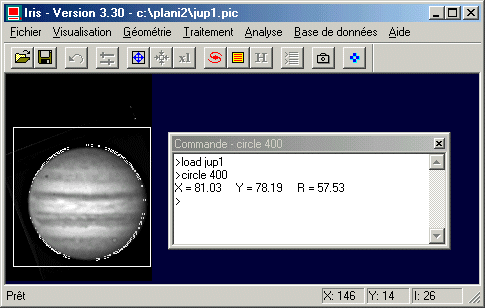
On retient que le centre du disque est aux coordonnées (81.0, 78.2) et que le rayon du disque est d'environ 57.5 pixels (rappel : le disque de Jupiter est aplati par la rotation aussi l'estimation du rayon est ici une moyenne).
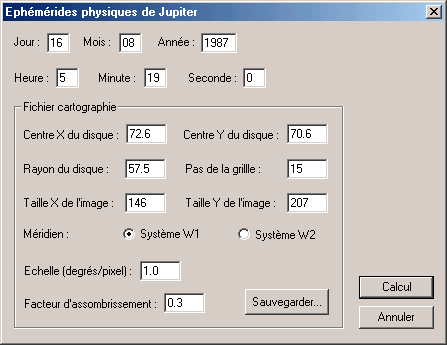
Pour définir les autres paramètres cartographiques nous allons nous aider de la boite de dialogue Ephémérides de Jupiter... qui peut être appelée depuis le menu Analyse. Remplissez cette boite de la manière suivante :
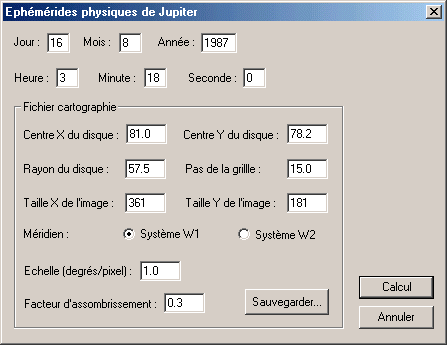
Vous devez tout d'abord entrer la date de l'observation (notez que les heures doivent être en TU - Temps Universel). Dans la zone Fichier cartographie, fournissez les coordonnées du centre du disque et son rayon, des paramètres déterminés à l'étape précédente (arrondissez au dixième de pixel, ce qui est largement assez précis).
Le pas de la grille correspond au pas du maillage d'un réseau de coordonnées que nous allons pouvoir plaquer sur le disque de la planète. Ici nous choisissons un pas de 15° en longitude et en latitude.
La taille de l'image est en principe renseignée directement si l'image traitée est en mémoire.
Dans le cas de Jupiter il faut définir le type de coordonnées en longitude (système I ou système II) du fait de la rotation différentielle de la planète. La période de rotation sidérale du système I qui s'étant de plus ou moins 10° de part et d'autre de l'équateur est de 9h50m30.003s. Le système II correspondant aux latitude plus élevées du disque et la période de rotation sidérale est de 9h55m40.632s. Ici nous choisissons le système I.
L'échelle (en degrés par pixel) définie la taille des images cartographiques. Ici nous adoptons 1 degré par pixel, ce qui est un bon choix la plupart du temps.
Enfin, le facteur d'assombrissement permet de compenser l'effet de la variation de l'albedo entre le centre et le bord du disque. La valeur de ce paramètre, qui est comprise entre 0 et 1, doit être choisie par essai successifs car elle dépend très fortement du type de traitement appliqué à l'image et du type de planète.
Une fois tout les paramètres renseignés, cliquez sur le bouton Sauvegarder... Iris vous demande alors de donner un nom de fichier de type LST. Par exemple choisissez le nom T1.LST pour ce fichier, que vous allez sauvegarder dans le répertoire de travail (c'est l'option que propose Iris dès le départ). Ce faisant vous venez de créer un fichier de type texte qui contient les paramètres fondamentaux de votre image JUP1. Il est facile de consulter le contenu de ce fichier avec un éditeur de texte (le WordPad de Windows par exemple) ou encore en utilisant la boite de dialogue Afficher les données du menu Analyse :
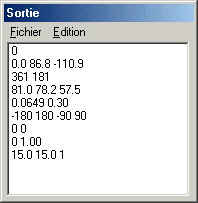
La structure de ce fichier généré automatiquement par Iris est strictement identique quelque soit le type de projection cartographique que nous allons utiliser. Le fichier T1.LST décrit plus spécifiquement un type de projection appelée Télescopique, qui correspond à l'aspect d'une planète observée avec un instrument d'astronomie.
Pour illustrer immédiatement l'usage du fichier de paramètre cartographique nous allons exécuter une commande qui affiche sur le disque de Jupiter une grille de coordonnées représentant les longitude et latitude planétaires. La commande s'exécute en mode commande en ligne et s'appelle GRID. Elle nécessite deux paramètres :
- le nom du fichier décrivant le projection cartographique, ici une projection télescopique. Ce nom de fichier sera bien sur ici T1 (il ne faut pas fournir l'extension .LST).
- l'intensité de la grille, un nombre compris entre 0 et 32767.
Mettons cela en application :
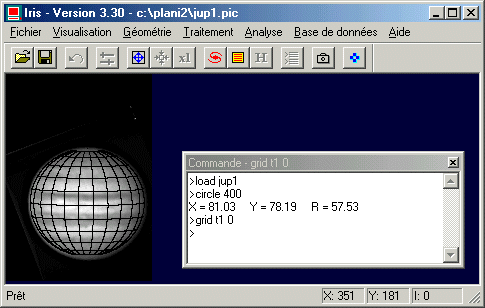
On remarque que le pôle nord est tourné légèrement vers l'observateur, ce qui a pour effet d'incurver légèrement les parallèles. Cet effet est déjà visible en examinant la courbure des bandes de Jupiter.
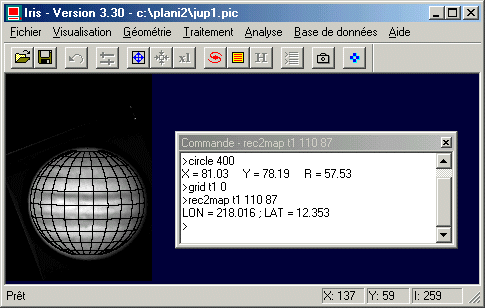
Supposons à présent que vous souhaitiez déterminer les longitude et latitude d'un détail du disque de la planète situé aux coordonnées image (110, 87). Vous devez pour cela utiliser la commande REC2MAP de la manière suivante :
REC2MAP T1 110 87
Le nom de la commande REC2MAP signifie que l'on convertie des coordonnées rectangulaires (X,Y) prises sur l'image en des coordonnées cartographiques (longitude, latitude), MAP étant un terme anglais dont la traduction en français est CARTE. Les paramètres de REC2MAP sont évident : on trouve tout d'abord le nom du fichier cartographie décrivant l'image en mémoire, puis ensuite, les deux coordonnées rectangulaires.
Il existe bien sur une fonction symétrique de REC2MAP qui permet de déterminer les coordonnées image de tout point défini par une longitude et une latitude. C'est la commande MAP2REC dont la syntaxe est très proche de MAP2REC. Par exemple :
MAP2REC T1 218.016 12.353
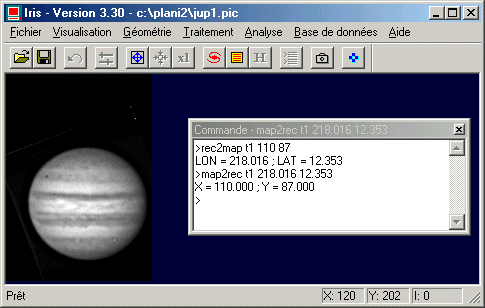
Les commandes REC2MAP et MAP2REC sont déjà des outils très précieux pour repérer les coordonnées vrai (planétaires) de détails morphologiques, même en restant dans une projection télescopique.
Nous allons détailler les 22 paramètres contenu dans un fichier cartographie. Celui-ci à la structure suivante :
PROJ
LAMP PHIP MERI
XW YW
XC YC RC
FL POWER
LONG1 LONG2 LAT1 LAT2
L1 L2
FLHEMI SCALE
LONGSTEP LATSTEP FLAG_T
Il est à noter que pour une projection cartographique donnée tous le paramètres ci-dessus ne sont pas nécessairement utilises. Un paramètre non utilisé prend la valeur 0.
Voici la description des paramètres :
PROJ : le type de projection cartographique utilisée. Iris reconnaît 17 projections différentes, spécialement sélectionnées pour leur utilités en astronomie. L'énumération de ces projections sera faite plus loin. Retenons ici que la projection ayant le numéro 0 correspond à la projection télescopique.
LAMP et PHIP : ces deux paramètres ne sont utilisés que pour la projection télescopique. Ils définissent les coordonnées apparentes (longitude et latitude) du pôle nord de la planète. Grâce à ces deux coordonnées il est possible de traiter un disque planétaire dont l'orientation est quelconque. Cependant dans un soucis de simplification, dans la présente version de Iris il est recommandé d'orienté l'axe polaire verticalement dans l'image (nous avons vu cela au début de cette leçon). Dans ces conditions LAMP ne peut prendre que deux valeurs : 0° ou 180° suivant que le pôle nord ou le pôle sud de la planète est orienté vers l'observateur. La valeur de PHIP est alors 90°-De où De est la latitude planétocentrique de la Terre (c'est la latitude du point de la planète depuis lequel on voit la Terre au zénith). La valeur de De est calculée automatiquement pour la date d'observation par Iris (+3.2° dans notre exemple). En outre, Iris calcule automatiquement les bonnes valeurs de LAMP et PHIP lors de la création du fichier cartographique et normalement vous n'avez pas à intervenir sur ces valeurs.
MERI : c'est la longitude du méridien central (système I ou II dans le cas de Jupiter) ramené dans un intervale compris entre -180° et 180°. Ici encore Iris à effectué le calcul pour vous pour la date de l'observation.
XW et YW : ces paramètres contiennent la taille de l'image en pixels. Ces paramètres ne sont utiles que pour la projection télescopique et lorsque cette projection est utilisée comme une sortie (voir plus loin l'usage de la fonction MAP).
XC et YC : les coordonnées, en pixels, du centre du disque de la planète dans une projection télescopique. Dans notre exemple on reconnaît les coordonnées calculées avec l'aide de la commande CIRCLE. Il faut remarquer que les coordonnées peuvent très bien se situer en dehors de l'image (cette situation se rencontre lorsque le disque de la planète est trop grand pour entrer en entier dans l'image CCD).
RC : le rayon équatorial de la planète en pixels dans le cas d'une projection télescopique.
FL : l'aplatissement de la planète. Dans le cas de Jupiter c'est aplatissement est de 0.0649. Dans le cas de la planète Mars l'aplatissement est de 0.
POWER : la puissance d'assombrissement centre-bord de la planète (utile uniquement pour la projection télescopique). Dans cette version de Iris on suppose que la planète n'a pas de phase et que l'assombrissement au limbe est une loi en puissance du cosinus de la longitude apparente. Ces limitations font que la correction de l'assombrissement centre-bord est une opération toujours délicate et en tout cas imparfaite. La valeur du paramètre POWER doit être estimée empiriquement (la valeur dépend par exemple du fait que vous avez ou non appliqué un filtre de rehaussement de contraste).
LONG1 et LONG2 : le domaine en longitude couvert par la carte. Pour une cartographie globale ces paramètres doivent prendre respectivement les valeurs -180° et 180°. Pour une cartographie régionale le domaine de ces paramètres peut être restreint.
LAT1 et LAT2 : le domaine en latitude de la carte avec LAT1<LAT2. Pour une cartographie globale la valeur de ces paramètres est respectivement -90° et 90°.
FLHEMI : un flag qui indique quel est l'hémisphère visualisé lors des projections cartographiques polaires (conique ou azimutale). La valeur est 0 pour l'hémisphère nord et 1 pour l'hémisphère sud.
SCALE : l'échelle moyenne ou équatoriale de la carte (cela dépend du type de projection) en degrés par pixel. Il faut faire attention à la valeur de ce paramètre lorsque le fichier cartographie est utilisé en sortie en raison de la taille de l'image générée. Par exemple, une image correspondant à une projection cylindrique entre -180° et 180° en longitude aura une dimension horizontale de 360 pixels si l'échelle est de 1 degré/pixel. Mais la taille sera de 3600 pixels si vous définissez par accident une échelle de 0.1 degré/pixel ! Un bon choix est généralement une échelle de 1 degré/pixel ou de 0.5 degré/pixel.
LONGSTEP, LATSTEP et FLAG_T : les deux premiers paramètres définissent le pas du maillage en degrés lors du tracé d'une grille de coordonnées sur une carte. Généralement le pas est compris entre 10° et 20°. Le paramètre FLAG_T est un paramètre réservé qui vaut toujours 1 ici.
A l'heure actuelle vous avez dans votre répertoire de travail un fichier .LST qui décrit la situation de votre image télescopique. C'est le fichier T1.LST.
Nous allons créer un nouveau cartographique qui va décrire la nouvelle projection que vous allez faire subir à votre image télescopique. Iris a ainsi besoin de deux fichiers cartographique pour effectuer les transformations : l'un, dit fichier d'entrée, décrit votre image actuelle, l'autre, dit fichier de sortie, décrit l'image après transformation. La fonction de Iris qui calcule la nouvelle carte s'appelle MAP. Sa syntaxe est la suivante :
MAP [FICHIER CARTO D'ENTREE] [FICHIER CARTO DE SORTIE]
Les deux paramètres de MAP ne sont autre que les fichiers .LST donnant la description de l'image avant et après transformation.
Créons dans le répertoire de travail un fichier cartographique de sortie qui décrit une projection cylindrique simple. Vous allez sauvegarder ce fichier sous le nom CYLIND.LST. Pour ce faire vous devez vous aider d'un petit logiciel de traitement de texte. Vous pouvez aussi partir du fichier T1.LST en le modifiant, mais en prenant garde aussi de ne pas l'écraser au moment de la sauvegarde. Voici le contenu du fichier CYLIND.LST :
1
0 0 0
0 0
0 0 0
0
0
-180 180 -90 90
0 0
0 1
15 15 1
Vous avez sûrement constaté que ce fichier est bien plus simple que celui décrivant la projection télescopique : de nombreux paramètres ont une valeur nulle. Le seul élément important est la premier paramètre (PROJ) qui prend la valeur 1, qui signifie que nous allons à faire une projection cylindrique simple (voir plus loin).
Vérifiez que vous avez bien chargé en mémoire l'image JUP1 et lancez la commande MAP :
MAP T1 CYLIND
Voici le résultat à l'écran :
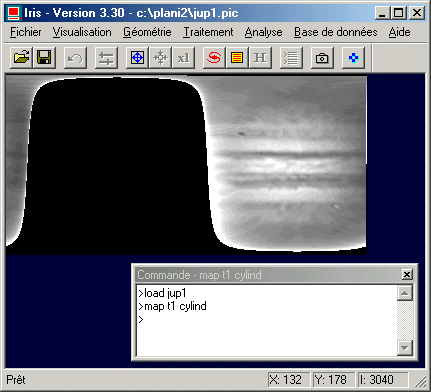
Iris à construit une portion de planisphère de la planète Jupiter en utilisant une projection dite cylindrique simple. Evidemment, la partie visible du planisphère correspond au demi-hémisphère visible sur le disque de l'image JUP1. On comprend cependant qu'il va être possible d'assembler plusieurs planisphères élémentaires de ce type, correspondant à des angles de rotations différents de Jupiter, pour constituer un planisphère complet. Il faut remarquer que Iris tente de restituer la surface de Jupiter dans la carte avec une échelle identique en tout point. La conséquence est que Iris doit interpoler fortement certaines régions qui sont très peu détaillés sur l'image originale en raison de l'effet de perspective. Cela est bien visible sur le limbe. En pratique ces zones sont trop déformées pour être vraiment utilisables, aussi faut-il les supprimer de l'image cartographique. On utilise pour cela la commande EDGE dont voici la syntaxe :
EDGE X1 Y1 X2 Y2
Les coordonnées images (X1, Y1) et (X2, Y2) définissent les coins opposés d'un rectangle à l'intérieur duquel l'image est conservée intacte. Tout point situé en dehors de ce rectangle prend l'intensité zéro. Dans le cas présent faisons par exemple :
EDGE 247 26 357 176
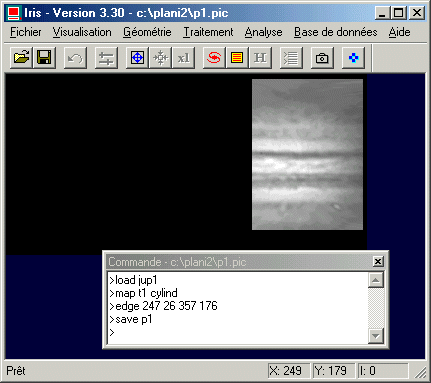
Le résultat est sauvegardé sous le nom P1.
La commande GRID fonctionne parfaitement avec la projection cylindrique, il suffit d'écrire :
GRID CYLIND 1500
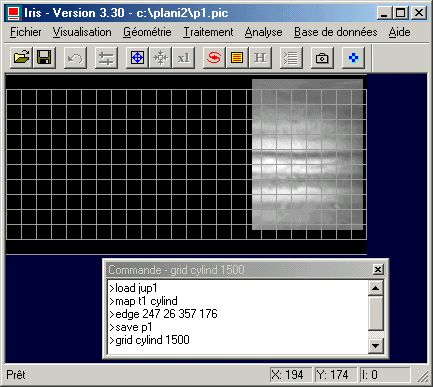
On remarque immédiatement la particularité géométrique de la projection cylindrique simple : l'échelle en degrés par pixel est identique en longitude et en latitude (le pas de la grille est égal suivant les deux axes).
Bien entendu les commandes REC2MAP et MAP2REC fonctionne aussi. Essayez par exemple :
REC2MAP CYLIND 290 67
Iris retourne pour ce point les coordonnées planétocentrique : Longitude=250°, Latitude -23°. Vous noterez s'en peine que la longitude 0° se situe au centre de la carte suivant l'axe X.
Nous pouvons à présent traiter la seconde image de la série : JUPI_2 :
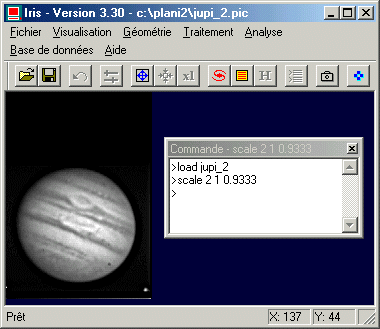
Tout comme pour l'image précédente il faut corriger le fait que les pixels ne sont pas carrés. Ensuite tourner la disque de 201° de manière à placer le pôle nord en haut de l'image, déterminer le centre précis du disque avec la commande CIRCLE, puis créer un nouveau fichier cartographique que vous aller appeler T2.LST, sachant que la date de prise de vue est le 16/08/1987 à 5H19TU. Vous allez vous aider pour cette dernière opération de la boîte de dialogue Ephémérides de Jupiter... du menu Analyse :
Voici le contenu du fichier T2.LST généré :
0
0.0 86.8 -37.1
146 207
72.6 70.6 57.5
0.0649 0.30
-180 180 -90 90
0 0
0 1.00
15.0
15.0 1
Il est dès lors simple de produire une nouvelle portion de planisphère :
MAP T2 CYLIND
Remarquez que le fichier décrivant la projection de sortie (CYLIND.LST) est bien sur toujours le même.
Voici la résultat après détourage de la partie utile de l'image, que vous sauvegardez sous le nom P2 :
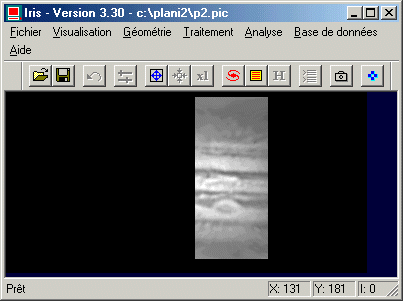
Il est aisée d'assemblée les portions de planisphère P1 et P2 en utilisant la commande MOSA. La procédure est la suivante :
LOAD P1
MOSA
P2 0 0 5
Le premier paramètre de la commande MOSA désigne le nom de l'image (P2) qui va être assemblée avec l'image actuellement en mémoire (P1). Les deux paramètres suivant définissent le décalage en pixels entres les deux images suivant les axes X et Y. Ici on désire que les images se superposent et donc les décalages sont nuls. Enfin, le dernier paramètre défini le type de fusion des parties communes des images. Ici on choisi un mode d'interpolation polynomial, qui est optimal dans le cas de figure (type = 5).
Les opérations sont reconduites avec les images JUPI_3, JUPI_4 et JUPI_5.
Les dates d'acquisitions des 5 images sont les suivantes :
JUPI_1 : 16/08/1987 - 3H18 TU
JUPI_2 :
16/08/1987 - 5H19 TU
JUPI_3 : 16/08/1987 - 6H38 TU
JUPI_4
: 17/08/1987 - 3H33 TU
JUPI_5 : 17/08/1987 - 4H59 TU
Voici pour résumer les portions de planisphère déterminées avec les 5 images de la série (images de P1 à P5) :
:




Pour assembler le planisphère complet vous devez faire (attention, la grille, si vous la tracé, fait partie de l'image, évitez donc de la dessiner avant de constituer la mosaïque) :
LOAD P1
MOSA P2 0 0 5
MOSA P3
0 0 5
MOSA P4 0 0 5
MOSA P5 0 0 5
Voici le résultat final :

Pour charger le planisphère complet de Jupiter, cliquez ici (fichier PLANI_JUP.ZIP - taille de 80 Ko).
Attention, ce planisphère a été calculé avec le système I des longitudes. Il n'est donc valable que pour une zone étroite de plus ou moins 10° par rapport à l'équateur. Pour pouvoir comparer la morphologie de jour en jour de Jupiter pour des latitudes plus élevées il est impératif de faire le calcul avec les système II des longitudes. Il faut faire très attention à ces considérations.