Leçon 20 : La cartographie planétaire (partie 2)

Cette leçon reprend les résultats de la leçon 19. Nous avons constitué un planisphère complet de Jupiter pour les dates du 16/08/1987 et 17/08/1987. La projection cartographique adoptée est la projection cylindrique simple. Il est facile à partir de cette projection de passer à une tout autre projection en créant le fichier cartographique adéquat Par exemple nous allons convertir notre planisphère en une projection télescopique originale qui va montrer Jupiter sous un angle particulier.

A partir du fichier T1.LST créez un nouveau fichier que vous aller appeler POLE.LST et qui contient les paramètres suivant :

0
0.0  45  50
361  181
81.0  78.2  57.5
0.0649  0.30
-180  180  -90  90
0  0
0  1.00
15.0  15.0  1

Puis exécutez la commande MAP de manière à convertir la projection cylindrique vers la nouvelle projection télescopique :

MAP  CYLIND   POLE

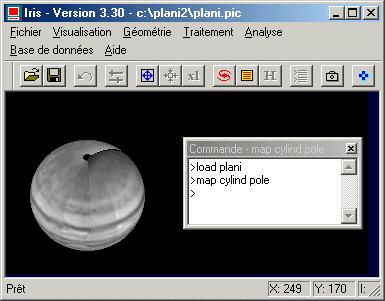
Pour tracer une grille sur cette image vous devez faire par exemple :

GRID   POLE   15000

En modifiant la valeur du paramètre MERI dans le fichier POLE.LST vous changez la valeur du méridien central dans l'image télescopique. Par exemple en faisant successivement MERI=30°, MERI=50°, MERI=70° vous obtenez les 3 images suivantes :

Vous pouvez produire autant d'images de ce type que vous voulez et avec le pas en longitude de votre choix. Il est possible ensuite de faire défiler en séquence ces images afin de produire une animation spectaculaire et fluide de la planète.

Iris peut traiter les problèmes cartographiques de la planète Jupiter, mais aussi de la planète Mars. Voici par exemple une image de Mars réalisée au télescope de 1 mètre du Pic du Mid le 26 décembre 1988 à 17h35m42s :

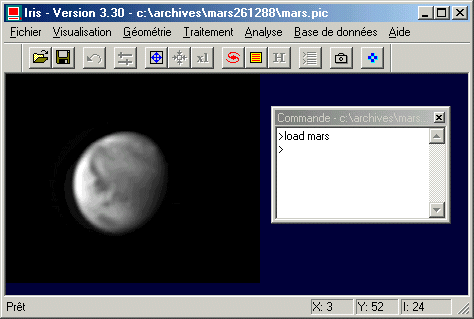
Pour télécharger cette image, cliquez ici (fichier MARS.ZIP - taille de 43 Ko)

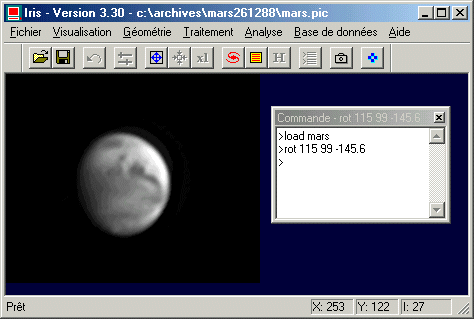
Tout comme pour Jupiter il est nécessaire d'amener l'axe de rotation vertical avec le pôle nord en haut :

Il faut à présent déterminer le centre du disque et son rayon avec l'aide de la commande CIRCLE. Notez dans l'exemple ci-après que le rectangle de sélection est défini de telle manière à éviter la partie de Mars située à la limite du jour et de la nuit (terminateur), ce qui fausserait le résultat. Dans le cas présent, la commande CIRCLE calcule le pourtour de la planète en n'utilisant dans le demi hémisphère droit :

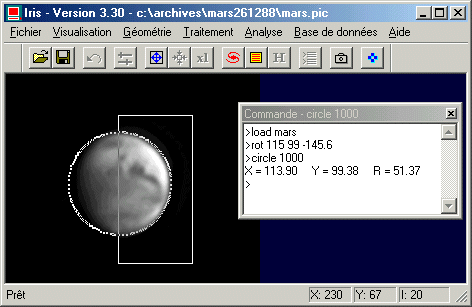
Pour créer le fichier décrivant la projection télescopique, appelez la boite de dialogue Ephémérides de Mars... depuis le menu Analyse. Remplissez cette boite de la manière suivante :

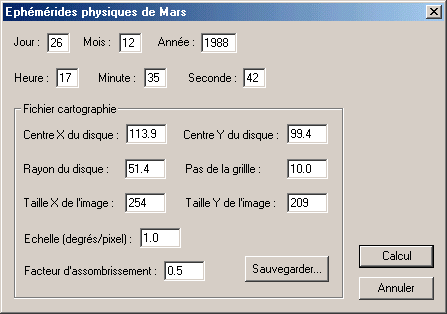
Sauvegardez le fichier cartographie en cliquant sur le bouton Sauvegarder... et donnez lui le nom TEL.LST.

Pour vérifier que tout va bien une sage précaution consiste à tracer la grille de coordonnées sur le disque :

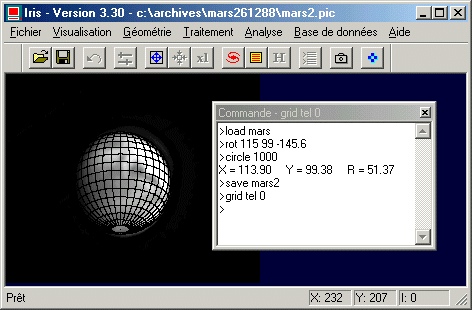
A titre de nouvelle vérification, repérez la formation martienne sinus sabaeus aux coordonnées images (131, 120). C'est par ce point que passe le méridien de longitude 0° sur Mars. Faite :

MAP2REC TEL 131 120

Iris retourne les coordonnées planétocentrique : Longitude=0.56° et Latitude=0.61°. Ce point se situe bien à l'origine des coordonnées de la planète Mars (à la précision de l'image près qui ne fait ici que 10 secondes d'arc de diamètre).

A ce stade vous pouvez bien sur tracer la carte de votre choix de la planète Mars en faisant par exemple :

MAP TEL CYLIND

Voyons à présent l'ensemble des projections cartographiques disponibles dans Iris. Rappel, le type de projection est contenu dans le paramètre PROJ du fichier cartographie. Voici les différentes valeurs possibles :

PROJ = 0 : projection télescopique, encore appelée projection oblique orthographique. Ce type de projection est important en astronomie car il correspond à l'image que donne le télescope des planètes. Les paramètres nécessaires à son utilisation sont LAMP, PHIP, MERI, XC, YC, RC, FL et POWER. Les paramètres XW et YW doivent aussi avoir des valeurs valides si le fichier de cartographie est utilisé en sortie.

PROJ = 1 : projection cylindrique simple. C'est l'une des projections cartographiques les plus populaires. On obtient une projection cylindrique en enroulant un cylindre autour de la sphère. La grille de coordonnées y est régulière et identique en longitude et latitude. L'ensemble de la planète peut être représenté. Il y a une distortion significative on longitude près des pôles. Le coté pratique de cette projection est qu'il existe une relation linéaire entre la taille des pixels image et les coordonnées planétaires, aussi est-elle recommandé comme projection de base à partir de laquelle d'autres projections seront construites. Les paramètres obligatoires sont LONG1, LONG2, LAT1, LAT2 et SCALE. Le planisphère en projection cylindrique simple ci-après montre la planète Mars en septembre 1988 réalisée avec le télescope de 1 mètre du Pic du Midi (image PLANI_MARS, pour télécharger cette image, cliquez ici - taille de 37Ko) :

PROJ = 2 : projection de Lambert cylindrique à surface égale. Les pôles sont moins déformés que dans le cas de la projection cylindrique simple et la projection respecte les surfaces. La représentation de toute la planète est possible. Les paramètres nécessaires sont LONG1, LONG2, LAT1, LAT2 et SCALE. Voici le planisphère de Mars représentée dans la projection de Lambert :

Pour effectuer une telle transformation vous devez écrire le fichier LAMBERT.LST suivant :

2
0 0 0
0 0
0 0 0
0 0
-180 180 -90 90
0 0
0 1
15 15 1

Puis modifier la projection cylindrique en utilisant la commande MAP :

LOAD PLANI_MARS
MAP CYLIND  LAMBERT
GRID LAMBERT 150

PROJ=3 : projection de Mercator. Il s'agit encore d'une projection dite cylindrique, mais probablement une des plus célèbre. Elle est dite conforme (cela signifie qu'elle conserve les angles entre tous les points de la carte), ce qui est très pratique pour les marins en navigation et pour tracer leur route (loxodromie). Elle est souvent utilisée comme standard par de nombreux organismes s'occupant de cartographie planétaire. Cette projection dilate notablement les latitudes élevées (les pôles sont en fait rejetés à l'infini), aussi il est fortement recommandé de limité à des latitudes inférieures à 60 ou 65°. A titre d'exemple, une zone de latitude 60° est dilatée d'un facteur 2 par rapport à la zone équatoriale, et une zone à 88° de latitude est dilatée d'un facteur 33 par rapport à la zone équatoriale ! Les variables nécessaires sont LONG1, LONG2, LAT1, LAT2, et SCALE. Noter que LAT1>-90° et LAT2<90°.

Ecrivons le fichier MARCATOR.LST :

3
0 0 0
0 0
0 0 0
0 0
-180 180 -60 60
0 0
0 1
15 15 1

Remarquez que l'excursion on latitude est limité à -60° et 60°. Puis

LOAD PLANI_MARS
MAP CYLIND MERCATOR

Voici la même projection Mercator avec le planisphère de Jupiter du 16/08/1987 :

PROJ = 4 : projection de Mercator transverse (le cylindre de projection est en contact avec les deux pôles). La projection est conforme et a l'avantage de ne pas distordre pôle. C'est à présent la région équatoriale qui est fortement déformée. Le méridien central est calculé automatiquement à partir de la moyenne des paramètres LONG1 et LONG2. Les paramètres indispensables sont LONG1, LONG2, LAT1, LAT1 et SCALE. Voici ce que donne cette projection à partir du fichier suivant :

3
0 0 0
0 0
0 0 0
0 0
-120 120 -60 60
0 0
0 1
15 15 1