Nouveautés de la version 5.30

Version 5.30 -  4 mars 2006

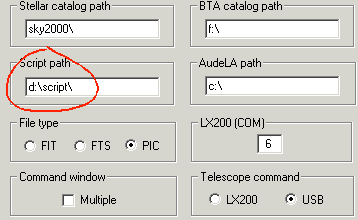
Vous pouvez à présent définir un répertoire dans lequel sont regroupés vos fichiers de script (commande RUN). Il faut pour cela ouvrir la boite de réglage du menu Fichier; puis remplir champ le chemin de script en désignant un répertoire valide :

Si le champ est vide, Iris cherche les scripts dans le répertoire de travail.

Exploitation des optiques fisheye

Voici une image fisheye typique :

Canon EOS 5D et objectif fisheye Peleng 8 mm f/3.5. Le Peleng est un objectif bas coût; mais aussi un très bon fisheye de 180° de champ.
La trame entière ci-dessus (réduite) montre comment est réalisée la projection fisheye sur la capteur Full-Frame du 5D.
Pour des détails sur les caractéristiques du fisheye Peleng, cliquer ici.

Iris V5.30 introduit un nouveau jeu de commandes de corrections géométriques (menu Géométrie) :

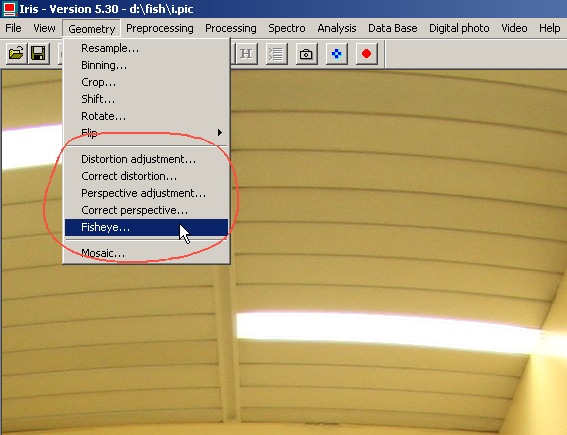
Lancer la commande Fisheye...  :

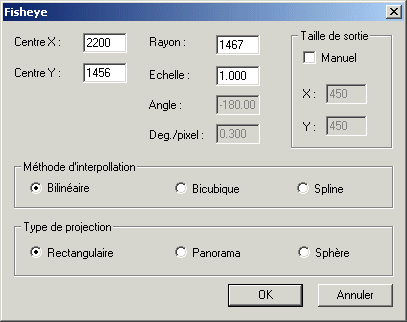
Entrer les coordonnées du centre du champ de l'image fisheye. Ici x=2200, y=1456. Fournir aussi la distance focale de l'objectif. Au besoin, essayer plusieurs valeurs afin de minimiser les distorsion après traitement (si vous travaillez avec une image en format réduit, multiplier la distance focale par le facteur de réduction). Choisir l'interpolation Bilinéaire pour un résultat rapide. Choisir la projection Rectangulaire. Cliquer sur OK. L'image fisheye sphérique est maintenant projetée sur un plan de front tangent à la sphère.

Recharger l'image fisheye et sélectionner un facteur d'échelle plus petit :

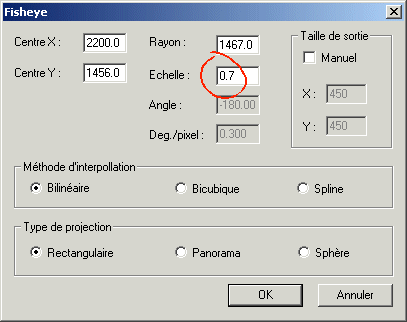
Facteur d'échelle de 0,7.

Vous pouvez encore ajuster la taille de l'image après transformation. Par exemple :

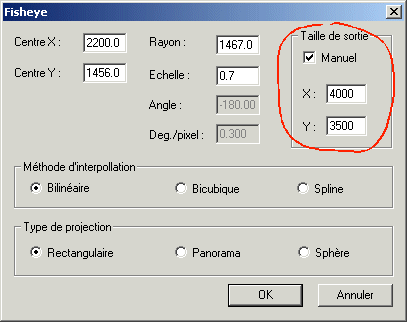
L'image finale a ici un support de 6000 x 3500 pixels (version réduite).

Pour le résultat final, après ajustement des paramètres, il est recommandé de choisir l'option d'interpolation Bicubique.

Cette technique d'échantillonnage de l'image permet de préserver les plus fins détails de l'image, tout en conservant un temps de calcul raisonnablement court. La méthode Spline donne un résultat encore meilleurs mais pas fondamentalement différent, pour un temps de calcul nettement plus long. On réservera l'option Spline au traitement d'images de taille relativement petite ou pour une touche vraiment finale.

Considerons à présent cette vue globale du ciel (l'objectif est orienté vers le zénith, l'image est prise depuis mon propre observatoire urbain) :

Canon EOS 5D + Peleng 8 mm fisheye. Depuis mon observatoire en terrasse.

Sélectionner l'option Panorama et entrer les paramètres suivants :

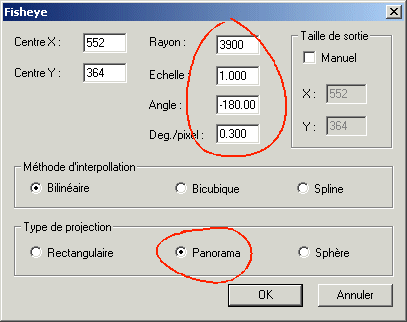
La figure suivante donne la signification de ces paramètres :

La paramètre Angle défini l'angle de position à l'origine de la future vue panoramique. Le paramètre Deg./pixel est l'échelle horizontale de la vue panoramique en degrés par pixels. Voici le résultat :

L'image panoramique.

 
L'angle de position est à présent de -80°.

Il est possible d'obtenir un résultat équivalent en utilisant le jeu de commande suivant depuis la console :

>LOAD FISHEYE_VIEW
>REC2POL2 552 364 390 -80 0.3
>MIRRORXY
>MIRRORX

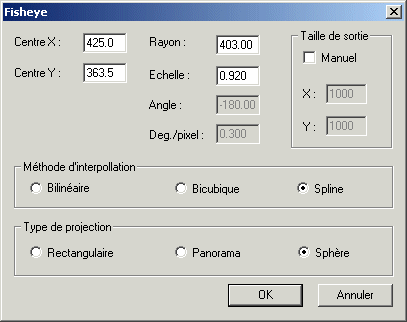
Essayez à présent l'option Sphère (bien sur, penser à charger en mémoire l'image fisheye originale en premier).

Les paramètres sont les coordonnées du centre de l'image fisheye, le rayon de cette image en pixels, et un éventuel facteur d'échelle.

Après la projection sphérique, la scène est comme si vous la voyez en reflection sur une sphère. Cette nouvelle projection offre des possibilités considérables lorsqu'on la couple avec les outils cartographiques de Iris (commande MAP).

Editer le texte suivant (par exemple en employant l'application WordPad) :

0
0  90  0
848 727
424 364 370
0 0
-180 180 -90 90
0 0
0 1
10 10 3

et le sauver dans un fichier ayant pour nom SPHERE.LST (c'est un exemple, l'import ant est l'extension qui doit être .LST). Pour simplifier, utiliser le répertoire de travail actuel. Ce fichier contient une liste de paramètres pour la famille de commandes MAP (cartographie). Voici la signification de ces paramètres :

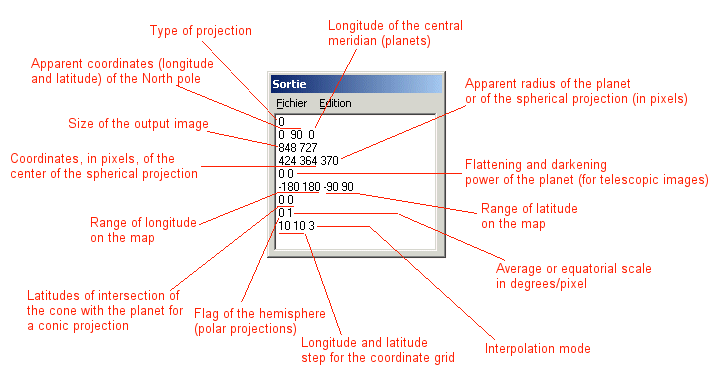
Pour une description complète de la commande MAP et de ces possibilités, cliquer ici. Pour quelques exemples d'application (en français), cliquer ici.

Par exemple, avec l'aide du pointeur de souris on a mesuré soigneusement que le centre de l'image sphérique se situé aux coordonnées X=424 et Y=364 (vous pouvez entrer des valeurs fractionnaires). Une autre valeur importante ici est le rayon de la sphère en pixel (R=370 dans l'exemple).

Le dernier paramètres du fichier de description est le mode d'interpolation utilisé pour synthétiser les images. Dans le présent exemple on utilise la valeur 3, qui signifie que l'interpolation est du type bicubique (c'est un bon choix pour la vaste majorité des applications). La valeur 2 correspond à une simple interpolation bilinéaire, et la valeur 4 correspond à une interpolation spline.

Charger la représentation sphérique de votre scène et lancer la commande suivante depuis la console :

>GRID SPHERE 0

Le premier paramètre indique le fichier de paramètres décrivant l'actuelle projection (ici une projection sphérique car la première valeur du fichier de description est 0). Le second paramètre est l'intensité de la grille de coordonnées tracée à l'écran. Voici le résultat :

Maintenant, éditer le nouveau fichier ASCII suivant :

0
0  140  0
848 727
424 364 370
0 0
-180 180 -90 90
0 0
0 1
10 10 3

et sauvergarder le sous le nom SHERE2.LST. La seule différence avec le fichier SHPERE.LST est la valeur de la latitude du pole nord (140° au lieu de 90°). Lancer la commande MAP de la manière suivante :

>MAP SPHERE SPHERE2

La syntaxe est très simple. Le premier paramètre est le nom du fichier de paramètre décrivant la projection de l'image à transformer. Le second paramètre est le nom du fichier décrivant la projection de destination. Ici, la projection de destination est encore sphérique, très semblable à la projection de départ, mais avec le pôle incliné d'un angle de 140°-90°=50°. Vous pouvez parfaitement tracer une grille de coordonnées sur l'image transformée :

>GRID SPHERE2 1500

Le résultat :

La sphère inclinée

La calculatrice de poche est à présent pratiquement vue de face (son contour n'est pas strictement rectangulaire, car elle ne se trouve pas à une distance proche de l'infini au moment de la prise de vue, ce qui créée un effet de perspective).

Editer une nouveau fichier de description de projection, et sauvegarder le sous le nom CYLIND.LST :

1
0  0  0
0 0
0 0 0
0 0
-90 90 -60 60
0 0
0 0.2
10 10 3

C'est la description d'une simple projection cylindrique (elle s'apparente aux projections panoramiques). Recharger l'image de la sphère de départ, puis

>MAP SPHERE CYLIND
>GRID CYLIND 2000

L'image couvre un domaine angulaire de -90° à 90°suivant l'axe
horizontal et +/-60° suivant la direction verticale (voir le fichier CYLIND.LST).

Il est facile d'inverser le traitement (après avoir ou pas modifier l'image de la projection cylindrique) :

>MAP CYLIND SPHERE

Il est aussi facile de synthétiser un panorama sur 360° en combinant plusieurs images fisheyes. Modifier le fichier CYLIND.LST en un fichier CYLIND2.LST de la manière suivante :

1
0  0  0
0 0
0 0 0
0 0
-180 180 -60 60
0 0
0 0.2
10 10 3

Noter le nouveau domaine de longitude (-180°, +180°).

Modifier aussi le fichier de départ décrivant la sphère initiale (donner à la modification le nouveau nom SPHERE3.LST):

0
0  90  90
848 727
424 364 370
0 0
-180 180 -90 90
0 0
0 1
10 10 3

Le méridien central est décalé de 90° (paramètre 4). Lancer alors

>MAP SPHERE3 CYLIND2
>GRID CYLIND2 2000

L'image actuelle occupe la première partie gauche d'une scène sur 360. Elle peut être complétée plus tard par mosaiquage avec des scènes supplémentaires.

Calculer a présent une projection sinusoïdale à patir de la projection cylindrique de 360°. Pour cela écrire dans votre disque dur la fichier SINUS.LST :

5
0  0  0
0 0
0 0 0
0 0
-180 180 -70 70
0 0
0 0.2
10 10 3

>MAP SPHERE SINUS
>GRID SINUS 2000

Votre image couvrant 180° plaquée sur une projection sur 360°.
Noter la distortion minimale le long du méridien central (c'est une caractéristique de la projection sinusoïdate)

Voici un dernier exemple, une projection polaire. Sauvegarder le fichier POLAR.LST avec le contenu :

7
0  0  0
0 0
0 0 0
0 0
-180 180 -90 90
0 0
0 0.4
10 10 3

puis

>MAP SPHERE POLAR

Près de 300 combinaisons de projections sont possibles. Vous pouvez aussi créer des animations, montrant pas exemple la rotation autour d'un point de vue, et bien plus. Ici quelques exemples de démonstration.

Correction de la distorsion optique

Considérer l'image suivante acquise avec un Canon EOS 5D et un zoom Canon 17-40 mm utilisé à la focale de 17 mm :

Un exemple de distorsion optique en barillet notable.

For corriger ce type de distorsion Iris calcul u décalage radial spécifique pour tous les pixels de l'image. La fonction calculé est un polynome du troisième ordre, caractérisé par ces coefficients A, B, C, et D. Ces coefficients sont spécifiques à un objectif donné, et peuvent être ré-utiliser pour traiter toutes les images acquises avec cet objectif. La forme de la fonction ajusté est :

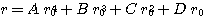
La paramètre D défini l'échelle de l'image finale. Si A=B=C=0 and D=1, l'image n'est pas modifiée. Les valeurs négatives pour les coefficients sont accéptées pour corriger la distorsion en coussinet. Il est possible de mélanger des coefficients ayant des valeurs négatives et positives. Par exemple, une valeur négative pour le coefficient A permet de compenser une distorsion affectant les pixels les plus extérieurs, alors qu'une valeur positive pour le coefficient C permet de corriger une distorsion en barillet au centre de l'image. Bien sur, le traitement doit s'appliquer à une image complète, et non pas à une portion.

Dans une première étape, l'estimation des coefficients peut être faite intéractivement. Lancer la commande Ajustement de la distorsion... du menu Géométrie, puis

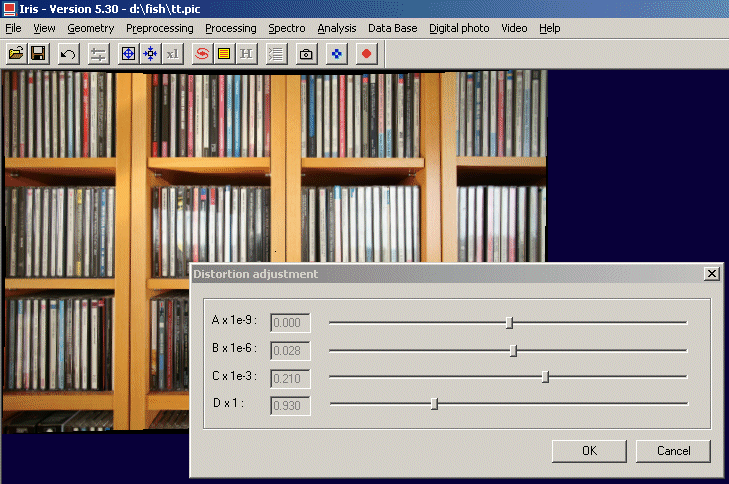
En minimisant la distorsion par simple examen visuel on trouve ici :: A=0, B=0.028.10^-6, C=0.210.10^-3, D=0.93. Pour une première évaluation, vous pouver travailler sur une image de taille réduite pour accélérer le calcul. Toujours par soucis d'optimisation de la vitesse de calcul, Iris se contente ici d'une interpolation bilinéaire.

Pour le traitement final, ouvrir la boite de dialogue Correction de la distortion... du Géométrie et sélectionner la méthode d'interpolation Bicubique pour un échantillonnage de qualité avec un effet négligeable sur la dégradation de l'image finale :

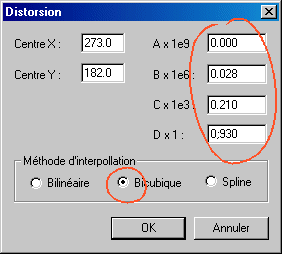
Si nécessaire, détourer le résultat final pour ne garder que la zone valide de l'image. Vous pouvez aussi superposer à l'image une grille qui peut vous aider à mieux  apprécier le résultat (commande Cadre... du menu Visualisation) - attention cette grille est permanente dans l'image, faite une copie avant sur votre disque dur :

L'image traitée.

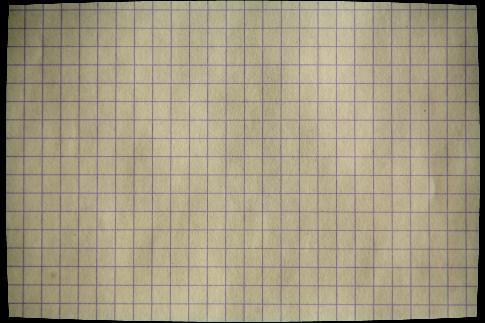
Le polynôme décrivant la distorsion peut être trouvé à partir de points relevés dans la photographie d'une grille régulière. Par exemple, voici un cadrillage vue au travers d'un objectif Canon 24-70 mm en position macro, équipant un Canon EOS 5D :

Avec l'aide du pointeur du pointeur de souris, relever les numéros de pixels correspondant à l'intersection de la grille, par exemple sur un axe horizontal, en partant du centre de l'image :

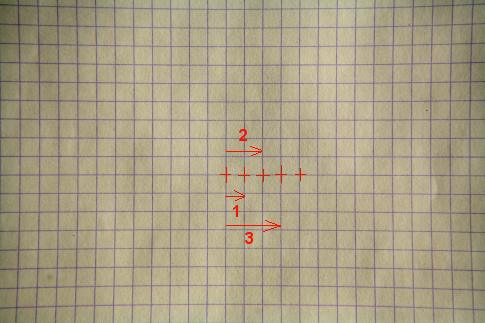
Inscrire le résultat dans un fichier texte sous la forme d'une liste à deux colonnes. La première contient les coordonnées relevées dans l'image. La seconde correspond aux coordonnées que l'on trouveraient  si l'optique ne présentée pas de distorsion. L'unité dans cette colonne n'a pas d'importance. Ici on choisi un pas régulier avec un incrément d'une unité d'une intersection de grille à la suivante. Ceci donne le contenu de fichier suivant :

0    0
167  1
331  2
498  3
664  4
830  5
995  6
1168 7
1334 8
1506 9
1678 10
1856 11
2033 12

Sauvegarder ce fichier dans le répertoire de travail, par exemple sous le nom grille.dat (seule l'extension est imposée).

Depuis la console, lancer la commande FITDISTOR avec les paramètres suivant :

>FITDISTOR GRILLE 4

La premier paramètre est le nom du fichier texte contenant les coordonnées mesurées dans l'image. Le second paramètre est le degré du polynôme qui est ajusté parmi les points mesurés. Voici le résultat dans notre exemple :

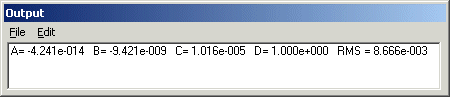
RMS est l'erreur quadratique de l'ajustement de la deuxième colonne du fichier. Plus la valeur de l'erreur est petite, meilleur est l'ajustement. Lancer la commande Correction de la distorsion... du menu Géométrie :

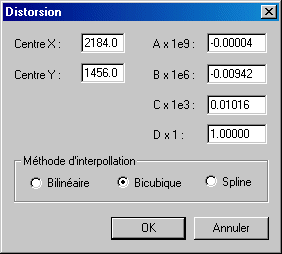
Tous les champs de la boite de dialogue sont automatiquement rempli. Cliquer sur OK pour traiter l'image. Voici le résultat :

Noter que dans la plus part des situations, un polynôme d'ordre 2, et éventuellement d'ordre 3, est largement suffisant (voir la petitesse du coefficient d'ordre 4 dans l'exemple).

Astuce 1 : la commande FIT est un petit utilitaire permettant d'ajuster un polynôme de degrés quelconque sur les données inscrites dans un fichier texte en deux colonnes. Par exemple :

>FIT GRILLE 6

Un fichier des résidus est créée automatiquement dans le répertoire de travail (OC.LST).

Astuce 2 : vous pouvez traiter séparément les couches R, G et B d'une image couleur, ce qui offre la possibilité de corriger le chromatisme latéral  Séparer votre image 48 bits en ces composantes R, G et B (commande SPLIT_RGB), adjuster la distorsion de chaque couche couleur, puis recombiner une image couleur (commande TRICHRO).

Correction de la perspective

Charger une image, puis lancer la commande Ajustement de la perspective.... du menu Geometrie :

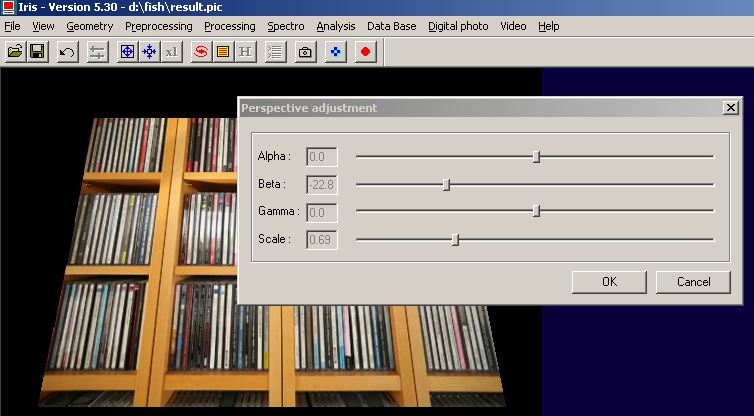
Sélection intéractive des paramètres de la perspective.

Voici quelques effets de perspective produits en fonction de la valeur des angles choisis :

Pour le traitement final, lancer la commande Correction de la perspective... du menu Geometrie et sélectionner l'option Bicubique. Vous avez aussi la possibilité de définir la taille de l'image finale (pour connaître la taille de l'image en mémoire, lancer la commande INFO depuis la console ou consulter la boite de dialogue Info image... du menu Fichier) :

 
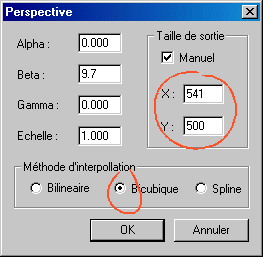
Le défaut de perspective à corriger (lignes fuyantes)...

...l'image après correction de l'effet de perspective.
Noter que la distorsion optique peut être corrigée au préalable (voir le paragraphe suivant).

Voici un autre exemple classique, sur une image de bâtiment :

Après l'usage de l'outil perspective, l'image ci-dessus a subit une très retouche visant à la tasser très légèrement verticalement. Le but était de maintenir un contour bien circulaire pour le lampadaire boule. L'opération est aisé en utilisant l'outil Changement d'échelle... du menu Géométrie. La facteur d'échelle appliqué suivant l'axe horizontal est de 1 (pas de modification) et de 0,96 suivant l'axe vertical :

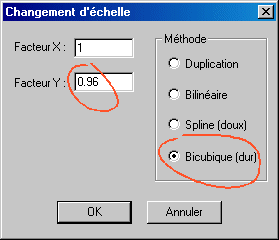
Le choix de l'interpolation bicubique permet de préserver un maximum de détails. Ce choix est à privilégier pour les images non astronomiques, mais en revanche il faut être plus prudent lorsqu'on travaille des images du ciel profond. Dans ce cas quitte à avoir une image un peu moins fine au final (pour un agrandissement), il vaut mieux choisir l'interpolation Spline qui produit moins d'artifact autour des étoiles.

Le dernier exemple est plus délicat car il fait appel à la fois au basculement et au balancement de l'image. Les paramètres sont cependant assez faciles à trouver en utilisant l'outil de perspective interactif. Le degré de correction de la perspective est de toute manière assez subjectif, fortement lié à l'appréciation de l'opérateur et à la destination de l'image.

Correction du vignettage optique

La commande de base est  CVIGNE2. Voici la syntaxe :

CVIGNE2 [IMAGE] [TEST]

[IMAGE] est le nom du fichier image à corriger. [FLAT] est l'image d'une scène la plus uniforme possible acquise dans les mêmes conditions que l'image à corriger (même objectif, même ouverture). Iris ajuste un polynôme de second ordre sur l'image "flat" et applique ce polynôme à l'image à traiter pour compenser l'effet du vignettage optique. Le résultat est affiché à l'écran après traitement. Exemple :

Image d'un écran blanc éclairé uniformément. L'image est acquise avec un objectif Canon de 500 ouvert à f/1,4.
Le vignetage optique est clairement visible (obscurcissement sur les bords). L'image est sauvegardée sous le nom FLAT (par exemple).

La méthode alternative consiste à utiliser les commandes EVIGN and CVIGN.

EVIGN

Charger l'image "flat" et lancer la commande  EVIGN (elle n'a pas de paramètres). Iris retourne dans la fenêtre de sortie les coefficients du polynôme ajustant le défaut de vignetage optique :

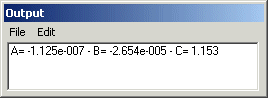
Dans le présent exemple, par rapport à la distance X relativement au centre de l'image, le vignetage est modélisé par l'équation :

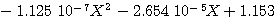
CVIGN [A] [B] [C]

Applique la correction de vignetage à l'image à traiter. Charger cette image, puis faire par exemple

>CVIGN -1.125e-7 -2.654e-5 1.153