ETAPE 2 - LA REDUCTION ASTROMETRIQUE
Nous allons relier les coordonnées (x,y) des pixels dans l'image IMG3 à des coordonnées équatoriales (AD, DEC) (nous ferons la même chose plus tard avec les images IMG1, IMG2 et IMG4). C'est le but de la réduction astrométrique.
Chargeons l'image IMG3 :
>LOAD IMG3
Lancer la commande Astrométrie automatique... du menu Analyse :

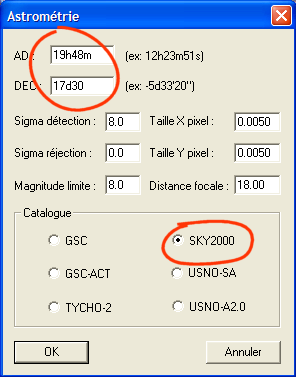
Entrer les coordonnées équatoriales du centre de l'image (les mêmes que celles adoptés à l'étape de recherche la distorsion optique). Vérifier que la taille des pixels et la distance focale sont correctes. Sélectionner le catalogue SKY2000. Finalement, cliquer sur OK.
Iris recherche alors automatiquement des étoiles en correspondance entre l'image photographique et la carte du ciel SKY2000. La réduction astrométrique est effectuée à partir de ces correspondances. Le logiciel entoure par des cercles les étoiles utilisées pour la réduction. Dans la fenêtre de sortie, le logiciel donne les paramètres astrométrique fondamentaux de l'image sous la forme d'un jeu de deux équations, une pour chaque axe de l'image :
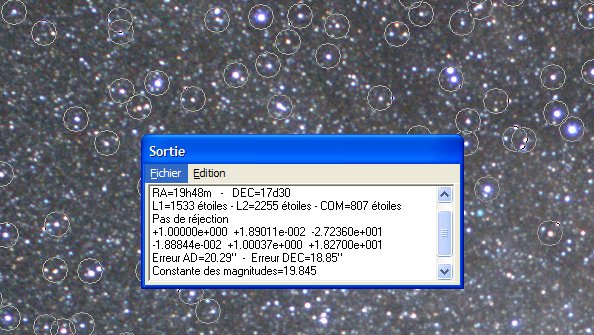
Cette matrices de 3x2 paramètres contient les éléments d'une transformation affine (translation, rotation, échelle) et se lit de la manière suivante :
A B C
D E
F
Les équations de cette transformation relient un point de l'image d'arrivée (x,y) à un point de l'image de départ sont (x',y') :
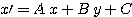
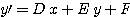
Les paramètres C et F correspondent à une translation respectivement suivant les axes X et Y.
Normalement Iris retourne les paramètres d'une matrice de rotation, translation, échelle de la forme :
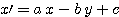
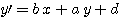
Dans notre exemple nous avons :
A = +1.00000
B = +0.0189011
C = -27.236
D = -0.0188844
E
= +1.00037
F = +18.270
On vérifiera que nous avons bien environ :
a = A = E
b= -B = D
c = C
d = F
L'angle de rotation f est relié aux paramètres par :
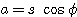
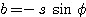
avec s le facteur d'échelle
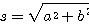
L'angle est donc donné par

Dans notre exemple, le facteur d'échelle étant très proche de l'unité nous pouvons trouver la valeur de l'angle de rotation avec une bonne précision en faisant simplement
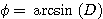
Nous évaluons cet angle à -1,08°. C'est la valeur déjà trouvée intéractivement à l'occasion de la recherche de loi de distorsion.
Noter que la fenêtre de sortie nous informe aussi que la réduction astrométrique permet de positionner les objets de l'image avec une précision de 20 secondes d'arc, ce qui n'est pas si mal vue la focale de l'instrument utilisé (focale de18 mm) et son champ.
Compte tenu de la distorsion initiale, il faut aussi souligner
que la correspondance entre les étoiles dans l'image et dans la carte synthétique
serait impossible. Il y a trop d'écart en effet entre la position attendue des
étoiles dans l'image et la position observée. Ceci souligne l'importance cruciale
de bien estimer la distorsion optique. Ici, le logiciel a
identifié 1533 étoiles dans l'image photographique, 2255 étoiles dans l'image synthétique
produite avec le catalogue SKY2000 et 807 étoiles communes. Ce sont ces 807
étoiles qui servent à réduire astrométriquement l'image (par la méthode des
moindres carrés). Si malgré la correction de la distorsion, le logiciel ne peut
pas trouver d'étoiles en correspondances entre l'image est le catalogue de référence
essayez de modifier les valeurs par défaut de sigma détection (sensibilité
à la détection des étoiles) et la magnitude limite du catalogue dans
la boite de dialogue Astrométrie.
Nous allons transformer notre image IMG3 de manière à ce que ces axes X et Y soient orthogonaux au système équatorial et que l'échelle et le centre d'image soient conformes à la réduction. Le jeu d'équation affine est utilisé pour cela. Ouvrir la boite Transformation affine... du menu Analyse :
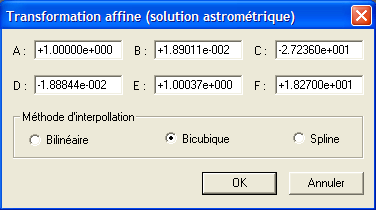
Les champs contenant les paramètres de la transformations affine sont déjà rempli du fait que l'on vient juste de faire la réduction astrométrique. On peut se contenter de cliquer sur OK. Noter dans le résultat que l'image est pivotée de 1° environ par rapport à l'original. C'est la différence la plus visible. Sauvegarder le résultat sous le nom ASTRO3 :
>SAVE ASTRO3
Nota : si vous faite la réduction astrométrique de l'image ASTRO3 vous aller constater que l'angle f a maintenant une valeur nulle.
A ce stade il est facile de voir que l'image est correctement réduite. La petite exploitation que nous allons faire immédiatement est déjà bien utile pour pointer les objets par leurs coordonnées et a quelques vertus pédagogiques.
Soit à identifier la position de l'étoile Altair. Les coordonnées équatoriales sont :
Alpha = 19h50m47s
Delta = +8°52'
Ouvrir la boite de dialogue Tracé de cercles de coordonnés... depuis le menu Analyse. Entrer les coordonnées de l'étoile (Altair) et les coordonnées du centre de l'image (toujours les mêmes depuis le début). Sélectionner aussi le type de projection cartographique. Choisir la projection gnomonique. Cette projection est très important car elle gouverne la position des étoiles dans une images photographiques du ciel (le plan du film ou du capteur électronique est tangent à la sphère céleste au niveau du centre de l'image). Sa particularité est que les grands cercles (équateur céleste, méridien) sont des droites dans l'image. Son inconvénient est de déformer considérablement l'aspect du ciel pour des angles de champs élevée (pour limiter ce problème dans les optiques du type fisheye, les opticiens produisent un défaut de distorsion volontaire qui compense en partie celui de la projection). Le fait d'avoir corriger la distorsion avec précision dans notre image conduit à une projection gnomonique quasi parfaite, ce qui autorise aussi la réduction astrométrique comme nous l'avons vu.
Cliquez sur les boutons OK correspondant pour tracer des cercles de coordonnées d'ascension droite ou de déclinaison :
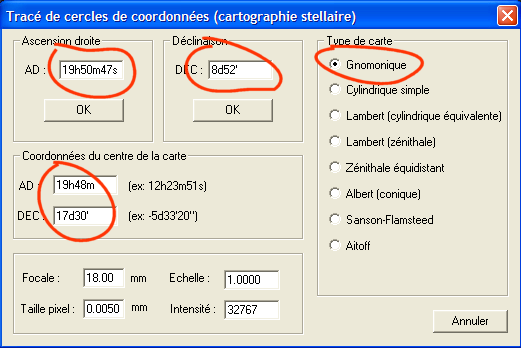
Voici le résultat (une petite portion de l'image centrée sur l'étoile Altair) :

L'étoile
Altair
Un autre exemple avec l'amas globulaire Messier 71 dans la constellation de la Flèche. Coordonnées de M71 :
AD = 19h53m46s
DEC = +18°47'

Pointage
de l'amas M71 après la réduction astrométrique (projection gnomonique).
Les caractéristiques astrométriques de l'image IMG3 sont entièrement définie par les coordonnées équatoriales du centre, la distance focale de l'instrument et la taille des pixels. Le nombre de ces paramètres est restreint, mais suffisant. A chaque image qui doit constituer par exemple un panorama il faut attacher un jeu de ces paramètres spécifique. Remarquez que ces paramètres sont fourni lors du tracé d' un cercle de coordonnées.
ETAPE 3 : LA PROJECTION CARTOGRAPHIQUE
L'image IMG3 est définie dans un repère gnomonique. Nous allons à présent projeter cette image sur un cylindre qui entoure la sphère céleste à l'équateur. Dans ce mode cartographique les cercles d'ascension droite et de déclinaison seront équidistant. C'est la carte la plus simple (on l'appelle parfois Carrée). Pour procéder, charger en premier l'image IMG3 puis invoquez la boite de dialogue Cartographie stellaire... depuis le menu Analyse :
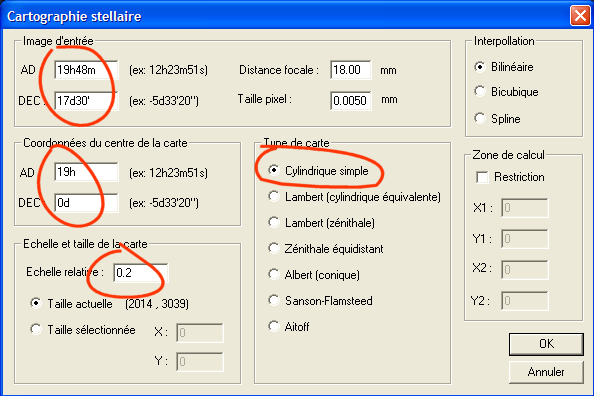
Les paramètres de l'image d'entrée sont relatifs à l'image en projection gnomonique. On retrouve les coordonnées équatoriales de son centre, la distance focale de l'optique et la taille du coté d'un pixel. C'est tout. Vous désignez le type de carte pour l'image résultat (image de sortie). Ici une projection cylindrique simple. Vous devez prendre ensuite une décision sur les coordonnées équatoriales qui se situerons au centre de votre image d'arrivée. Dans notre exemple le point situé au centre de l'image aura une ascension droite de 19h00m et une déclinaison de 0°00'. Enfin, nous définissons un facteur d'échelle relatif. Si vous désirez une image de sortie ayant une échelle moyenne identique à l'image d'entrée, choisissez la valeur 1,0 pour le facteur d'échelle. Pour notre exemple nous adoptons un facteur de 0,2, si bien que la distance linéaire entre deux étoile sera réduite d'un facteur 0,2 entre l'entrée et la sortie. Notre champ apparaîtra plus petit. En revanche, la taille de l'image de sortie est ici la même que l'entrée (2014 x 3039 pixels). Notre image d'entrée projetée dans le nouveau repère n'occupera donc qu’une fraction de la surface du support de sortie. Cliquez sur OK pour lancer le calcul.
Ci-après, un extrait du résultat :

Extrait
de l'image de sortie, en projection cylindrique simple.
Le réseau de coordonnées a été dessiné avec la fonction Tracé des cercles de coordonnées... Remarquer que ce réseau est constitué de droites. Les indications d'ascension droite et de déclinaison ont été ajouté dans un second temps avec un logiciel d'infographie (l'image peut être exporté depuis Iris en utilisant par exemple la commande SAVEBMP). Il faut bien préciser les conditions de tracé du réseau de coordonnées, par exemple ci-dessous pour l'ascension droite 20h00m et la déclinaison 10°00' :
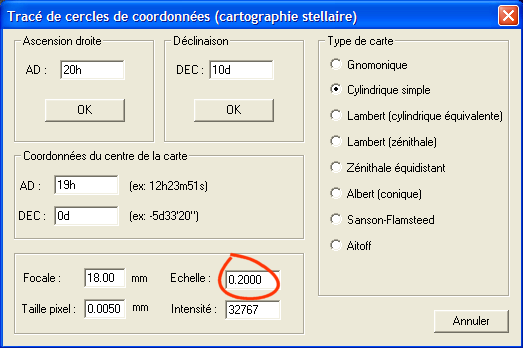
Le centre de l'image indiqué dans la boite de dialogue est celui décidé lors de la réalisation de la projection cylindrique (19h, 0°). Notez, que le facteur d'échelle doit aussi être précisé en cohérence avec celui adopté lors du calcul de la carte (Iris rempli ce champ pour vous). Penser encore à définir le type de carte correct.
Compte tenu du facteur de réduction utilisé (0,2 x), un grand espace autour de l'image produite ne contient pas d'information. Vous pouvez restreindre le domaine de calcul dans l'image d'arrivée dans une fenêtre dont on peut fixer la taille en définissant les coordonnées de deux coins opposés :
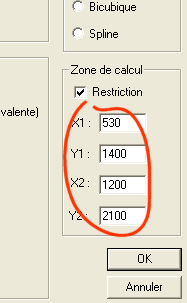
La taille de l'image de sortie est inchangée. La différence est que l'image n'est calculée dans l'image de sortie que dans la surface de la fenêtre que nous venons de définir. Ceci permet d'accélerer les calculs et au besoin de détourer la seule partie jugée utile de l'image (ellimination de certains phénomènes de repliement lors du calcul).
Depuis la boite de dialogue de cartographie stellaire vous avez aussi la possibilité de définir la dimension de l'image de sortie. Par exemple, en faisant
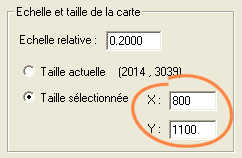
vous obtenez

Transformons à présent l'image ASTRO3 (la recharger en mémoire) dans une projection dite "cylindrique équivalente" ou encore de "Lambert cylindrique". Le cylindre de projection est tangent à l'équateur de la sphère avec des latitudes projetées radialement. Une propriété importante de cette projection, c'est de là que vient le terme "équivalent", est la conservation les surfaces. Ceci préserve la précision photométrique lorsqu'on intègre le signal d'une source étendue. Les régions polaires sont part ailleurs comprimées, ce qui permet de les visualiser dans une image de taille raisonnable. Par exemple faire :
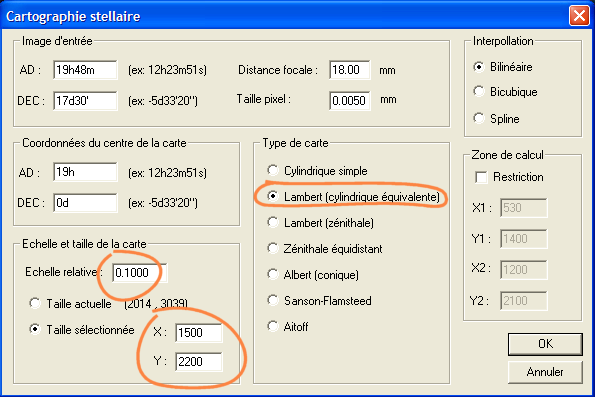
Le résultat :
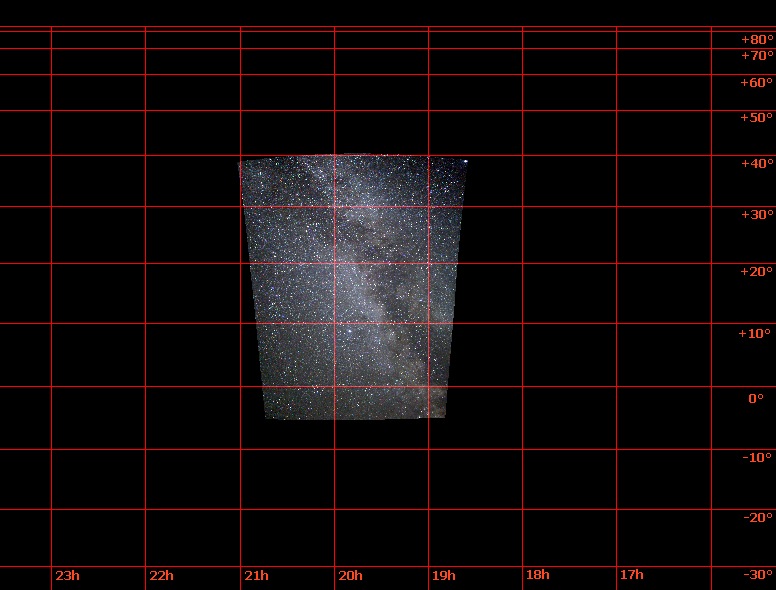
Expérimentons la projection de Lambert zénithale :
>LOAD ASTRO3
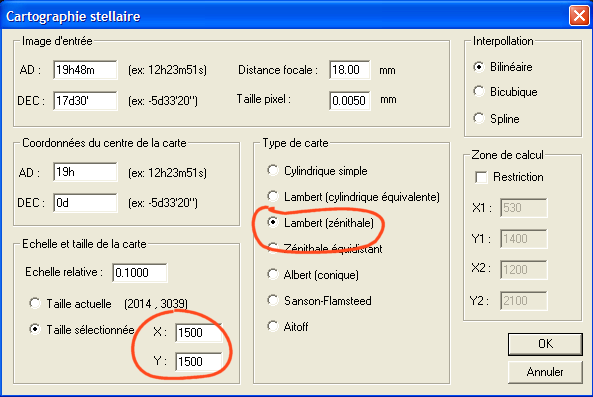

Projection
de Lambert zénithale.
Le pôle est au centre de cette projection zénithale (ou azimutale). Dans la version de Lambert les surfaces sont conservées. L'ensemble de la sphère céleste peut être représentées, mais avec une très forte déformation du demi-hémisphère opposé.
Dans la projection zénithale équidistante les cercles de déclinaison de pas identiques sont espacés par des intervalles égaux dans la carte :

Projection
zénithale équidistante.
Dans une projection conique, l'image est projetée sur une surface conique dont le sommet contient l'axe polaire et dont le point de contact avec la sphère céleste se situe à la déclinaison Theta. Vous devez entrer cet angle Theta si la projection conique est demandée. La grille d'ascension droite est représentée par des droites qui partent de l'apex du cône. Les cecles de déclinaison sont des arcs concentriques. Ce type de projection est pratique pour représenter des régions intermédiaires entre le pôle et l'équateur avec une faible déformation. Dans la projection conique de Alber les surfaces sont conservées. Voici un exemple, avec un point de contact du cône proche du centre de l'image :
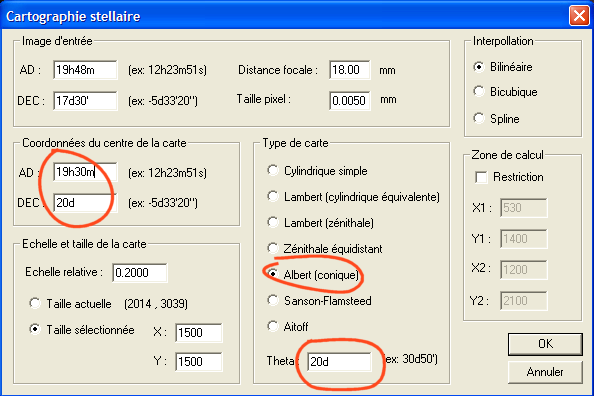
l'image ASTRO3 dans une projection conique prend l'aspect :

Les projections Sanson-Flamsteed et Aitoff sont particulièrement adaptées pour une représentation globale de la sphère céleste. Les deux projections conservent les surfaces. La projection Aitoff (parfois appelée Hammer-Aitoff) distort modérément les régions polaire. C'est une projection très classiquement utilisée pour montrer l'ensemble de la voûte céleste.
Exemple :
>LOAD ASTRO3
puis
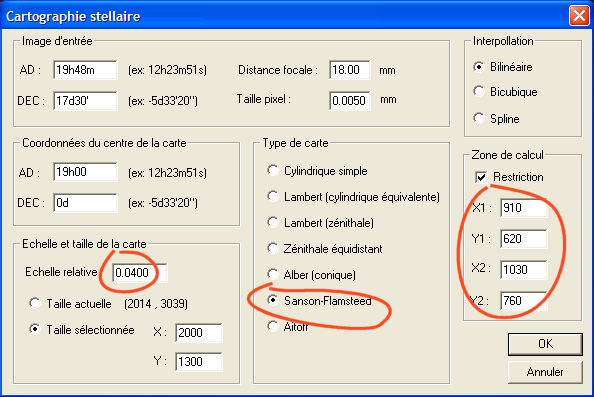
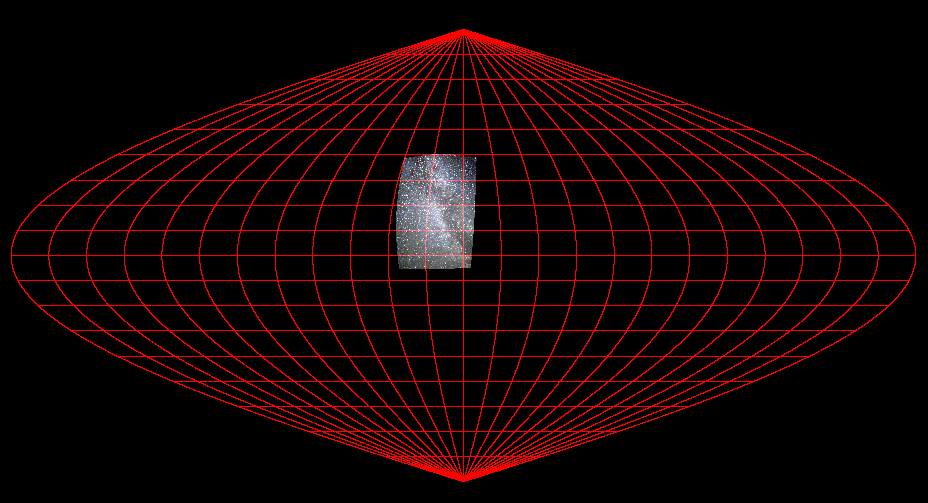
La
projection Sanson-Flamsteed. Remarquer la surface couverte par notre image obtenue avec
une focale de 18 mm par rapport à la surface totale du ciel.
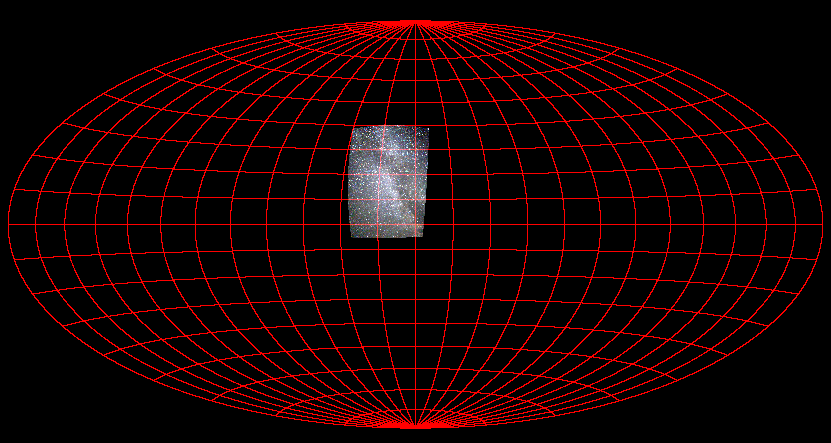
Projection
Hammer-Aitoff.
ETAPE
4 : L'ASSEMBLAGE D'UN PANORAMA
L'assemblage d'images grand-champs du ciel avec les logiciels d'infographie est une vraie gageure, avec à la clef un résultat incertain. Le raccord entre les images est quasi impossible entre des images dont les plan de projection changent d'une vue à l'autre. A ceci s'ajoute les problèmes de distorsion optique.
Les puissantes fonctions de correction de distorsion et de cartographie que nous avons évoqués plus haut permettent de réaliser de manière simple et rigoureuse de vastes mosaïques du ciel sans avoir le moindre besoin d'ajuster le raccord entre les images. Pour le démontrer nous allons réaliser une mosaïques du ciel à partir des images FIELD1, FIELD2, FIELD3 et FIELD4.
Nous avons déjà montrer comment réduire astrométriquement l'image FIELD3. Les mêmes opérations sont à reconduire pour les trois autres images.
Vous devez en premier corriger la distorsion optique de chaque image avec la commande Correction de la distorsion... du menu Géométrie. Vous n'avez pas recalculer les paramètres A1, A2 et A3 : ceux trouvé pour l'image FIELD3 s'appliquent sans problème. La correction de la distorsion de notre jeu d'image ne prend donc que quelques secondes. Faire :
>LOAD FIELD1
Appeler la boite de dialogue
Correction de la distorsion... du menu Géométrie et cliquer sur
OK sans changer les paramètres A1, A2 et A3
>SAVE
IMG1
>LOAD FIELD2
Appeler la boite de dialogue Correction
de la distorsion... du menu Géométrie et cliquer sur OK
>SAVE
IMG2
...et ainsi de suite.
La séquence IMG1, IMG2, IMG3 et IMG4 correspond à notre jeu d'images couleur corrigée du défaut de distorsion optique.
Vous devez ensuite estimer les coordonnées équatoriales approximatives du centre de chaque image. Pour notre séquence nous avons :
Image 1 : AD = 18h25m, DEC = -21°56'
Image 2 : AD =
19h00m, DEC = -6°50'
Image 3 : AD = 19h48m, DEC = +17°30'
Image 4 : AD
= 20h42m, DEC = +39°54'
A titre de rappel, voici la séquence de réduction astrométrique de la première image :
>LOAD IMG1
Lancer la commande d'Astrométrie automatique depuis le menu Analyse :
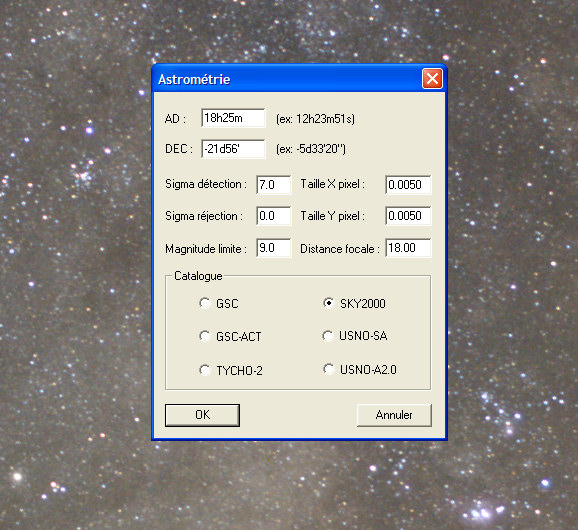
Rappelez-voius que si Iris vous informe qu'il ne trouve pas d'étoiles en commun entre l'image et le catalogue, alors modifier dans la boite de dialogue Astrométrie la valeur sigma de détection (sensibilité à la détection des étoiles) ou la magnitude limite des étoiles extraites du catalogue, puis refaire un essai.
Continuer par la transformation affine (commande Transformation affine... du menu Analyse) :
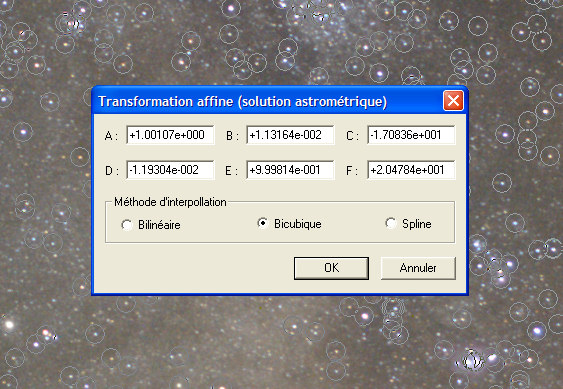
Enfin :
>SAVE ASTRO1
Reconduire les mêmes opérations pour les autres images, la seule précaution à prendre étant de modifier les coordonnées équatoriales du centre de l'image.
Vous disposez à présent des images ASTRO1, ASTRO2, ASTRO3 et ASTRO4.
Nous allons par exemple assembler les images ASTRO2 et ASTRO3 dans une projection du type Aitoff avec la pleine résolution pour juger la qualité du raccord.
Projetons en premier l'image ASTRO2 :
>LOAD ASTRO2
puis
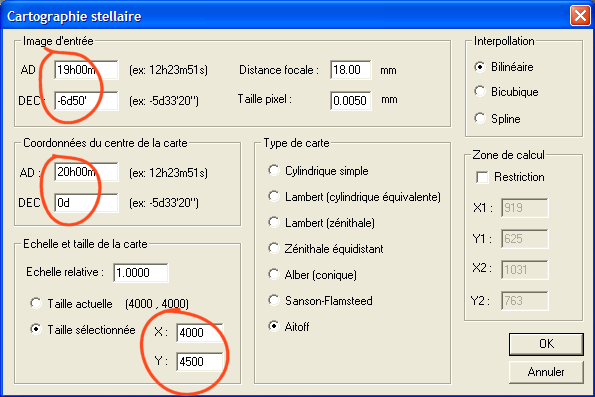
Remarquez que nous avons redéfini la taille de l'image de sortie. Elle est ici très grande pour que se support puisse contenir les deux images projetées dans la même carte avec un centre commun choisi à la l'ascension droite 20h00m et à la déclinaison 0°00'.
Au terme du calcul, sauvegardez le résultat intermédiaire
>SAVE PANO2
Calculons maintenant la projection de l'image ASTRO3 :
>LOAD ASTRO3
Nous modifions seulement les coordonnées du centre de cette image d'entrée. En revanche, nous ne touchons pas au centre commun entre les images dans la projection de sortie (AD=20h00m, DEC=0°) :
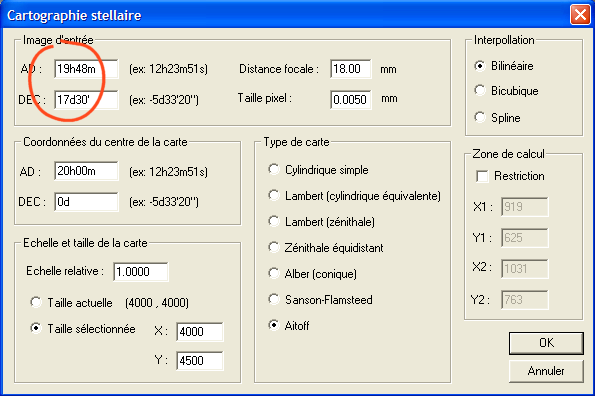
>SAVE PANO3
Il nous ne reste plus qu'à fusionner les images PANO2 et PANO3. Pour cela vous pouvez par exemple utiliser l'outil Mosaïque... accessible depuis le menu Géométrie :
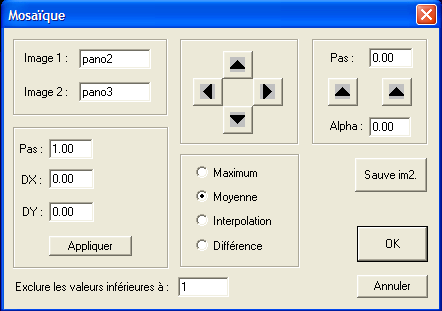
Si tout c'est bien passé, il n'y a pas de décalage entre les images. Contentez-vous de cliquer sur OK. Vous venez d'achever un panorama contenant deux grandes images de la Voie Lactée.
Examinons une petite partie des images PANO2 et PANO3 dans une zone où elles se chevauchent :

Extrait
de l'image PANO2.

Extrait
de l'image PANO3 pour la même région du ciel.
A l'évidence, dans les zones communes, les deux images se ressemblent. Seules les aberrations optique de notre objectif grand-champ modifie l'allure des étoile. L'image ci-dessous est un détail la fusion des images PANO2 et PANO3 pour la zone qui nous concerne :

Fusion
des images PANO2 et PANO3.
Il n'y a pas de dédoublement des étoiles. L'illusion qu'il s'agit d'une même image est très bonne alors qu'il s'agit d'une construction à partir de deux images distinctes. Le trait sombre horizontale dans la partie inférieure droite est un problème classique de bordure (cette bordure n'est pas nette dans l'une des images). La commande FILL2 peut aider à gommer les partie de l'images qui n'ont pas un bord "net", c'est à dire ne tombant pas brutalement du niveau nominal à la valeur zéro (remplissage avec des zéros d'une zone délimité par un rectangle de sélection à la souris). Vous pouvez obtenir alors des bordures franches et des raccords sans artéfacts.
Une autre solution pour obtenir des bords d'images abrupts consiste à utiliser la commande PANO_EDGE, spécialement écrite pour cela. La syntaxe est
PANO_EDGE [SEUIL]
SEUIL est un paramètre qui définir l'intensité valide juste en dehors de la zone de validité de l'image. Généralement, une petite valeur pour ce paramètre est recommandée. Par exemple essayer :
>PANO_EDGE 1
(la détection du bord d'image se fait en ajoutant juste un ADU à la valeur nulle).
Exemple pour notre jeu d'images:
>LOAD ASTRO1
>PANO_EDGE 1
>SAVE
ASTRO1
>LOAD ASTRO2
>PANO_EDGE 2
>SAVE ASTRO2
>LOAD
ASTRO3
>PANO_EDGE 3
>SAVE ASTRO3
>LOAD ASTRO4
>PANO_EDGE
4
>SAVE ASTRO4
Il demeure bien sur de votre responsabilité d'harmoniser le niveau entre les images pour que les raccords se produisent sans effet d'escalier. Ceci passe par un traitement rigoureux des images (en particulier la correction flat-field) et au besoin, par un usage de l’outil d'uniformisation du fond de ciel (voir ici par exemple).

La
fusion des images PANO2 et PANO3 après un détourage avec la commande PANO_EDGE.
Il est instructif de produire un décalage volontaire de 3 pixels suivant l'axe horizontal entre les images PANO2 et PANO3 puis de les fusionner :

Les
images PANO2 et PANO3 avec un décalage accidentel horizontal de 3 pixels.
L'effet est immédiatement visible dans le panorama à la jonction des composantes. La distorsion optique présente dans les images originelle représente plus de 10 pixels dans certaines parties du champ. Les erreurs de projection initiales entre les images élémentaires peuvent atteindre 20 à 30 pixels; On comprend toute l'importance d'avoir corrigé la distorsion puis de disposer d'un outil cartographique pour réaliser une projection dans un repère commun.
Pour fusionner une séquence d'image devant constituer le panorama final vous pouvez utiliser l'outil Mosaïque comme nous l'avons vu, en procédant deux par deux images (et en s'abstenant de produire le moindre décalage entre les images). Vous pouvez aussi utiliser les commandes PANO_MAX et PANO_MEAN. La première commande fusionne les images en ne conservant que les pixels d'intensité maximum dans les zones de recouvrement (c'est cette fonction qui a été utilisée ici car le raccord en intensité n'est pas parfait dans la séquence traitée, et PANO_MAX a tendance à atténuer ces défauts). La commande PANO_MEAN moyenne les intensités dans les zones de recouvrement. Les intensités nulles ou négatives ont alors une importance particulière dans le sens où elles ne sont pas prise en compte par le calcul. Par exemple supposons que dans une zone de recouvrement nous ayons pour une image l'intensité 100 et pour une autre image l'intensité 0 (car l'image n'est pas définie à cet endroit de la projection). Une moyenne simple donnerait l'intensité 50, qui ne reflète pas la réalité. Mais comme PANO_MEAN exclu du calcul les valeurs égales ou inférieures à 0, alors le niveau finalement calculé est 100, ce qui est proche de la réalité.
La syntaxe des commandes de fusion est :
PANO_MAX [NOM] [NOMBRE]
PANO_MEAN [NOM] [NOMBRE]
NOM est le nom générique des images individuelles du panorama. NOMBRE est le nombre d'images élémentaires.
Par exemple, pour notre exemple nous pouvons faire :
>PANO_MAX PANO 4
L'image après est un panorama réalisé avec les 4 images disponibles dans une projection équatoriale de Lambert (les coordonnées équatoriales du centre du panorama sont (AD=20h, dec=0°) :

Cliquer
sur l'image pour voir une version agrandie.
Voici encore nos 4 images dans une projection de Hammer-Aitoff, qui permet d'apprécier la surface couverte par rapport à la surface totale du ciel :

Cliquer
sur l'image pour voir une version agrandie.
Un détail de notre projection Hammer-Aitoff, qui montre l'efficacité de celle-ci pour visualiser un large domaine de déclinaison sans une déformation excessive des constellations :

Cliquer
sur l'image pour voir une version agrandie.
PRECEDENT SUIVANT RETOUR PAGE IRIS