Méthodes de mesure de la réponse instrumentale et de la transmission atmosphérique

Christian Buil
Castanet-Tolosan Observatory

1. L'enjeu

Le signal spectral brut enregistré par le détecteur d’un spectrographe est toujours fort loin de refléter celui réellement envoyé par la source mesurée.

La raison est que lumière doit traverser de très nombreux filtres spectraux avant qu'elle ne soit effectivement enregistrée. Ces filtres sont des éléments qui atténuent certaines couleurs au détriment d'autres. Au final, si rien n'est fait, le profil spectral brut observé n'est généralement pas exploitable tel quel, tellement il est distordu par rapport à la réalité.

Dans l'ordre, lorsqu’on observe une étoile, les éléments atténuateurs rencontrés sont :

- l'atmosphère terrestre (extinction) ;
- l'optique du télescope (miroirs, lame de fermeture, ...) ;
- l'optique du spectrographe (lentilles, réseau, ...) ; - le détecteur (variation spectrale du rendement quantique).

On peut distinguer deux catégories :

Catégorie 1 : les atténuateurs dont l'effet varie en fonction du temps, de l'endroit du ciel visé, du site d'observation.

Catégorie 2 : les atténuateurs qui sont au contraire stables en fonction de ces paramètres.

L'extinction atmosphérique fait bien sur partie de la première catégorie. Par exemple, suivant que l'étoile est observée proche de l'horizon ou au zénith, le profil spectral apparent de l'astre sera très différent. Cet ainsi que l'atmosphère atténue plus le bleu que le rouge et que cet écart augmente d'autant plus vite qu’on vise proche de l'horizon.

Dans une très large mesure, la transmission des optiques et la réponse spectrale du détecteur peuvent être rangées dans la catégorie 2. Ce sont des constantes instrumentales (ces paramètres sont figés par construction).

Il y a un effet cumulatif lorsque la lumière rencontre tous ces éléments. L'atténuation globale est égale au produit des atténuations élémentaires.

Les éléments appartenant à la catégorie 2 sont responsables de la réponse instrumentale. Il s’agit d’une courbe, tracée en fonction de la longueur d'onde, qui indique comment l'ensemble instrumental atténue telle couleur par rapport à telle autre.

Il est assez rarement utile de connaître la réponse instrumentale et la transmission atmosphérique en valeur absolue. Par exemple, savoir qu'à la longueur d'onde de 500 nm la moitié des photons est bloquée par l'instrument et l’atmosphère nous importe assez peu.

En revanche, prendre conscience que l'instrument et l'atmosphère atténuent deux fois plus le spectre réel de l'étoile à 400 nm qu'à 500 nm est bien plus important. En valeur relative cela signifie que l'atténuation est de 1 à 500 nm et de 0,5 à 400 nm. C'est cette dépendance en fonction de la longueur d'onde du rendement global du système d’observation (instrument + atmosphère) que nous cherchons ici à évaluer.

Voyons l'enjeu sur un exemple numérique.

Supposons une étoile nous envoyant hors atmosphère un flux lumineux de 30 à 400 nm et de 40 à 500 nm (peu importe les unités de flux).

Le ratio d'intensité vrai entre 400 nm et 500 nm est donc de 30 / 40 = 0,75. Cette valeur a importance astrophysique. Elle peut par exemple nous informer sur la température de l'astre. Sommes-nous capables de trouver ce rapport avec notre instrument ? C'est toute la question.

On sait que celui-ci atténue d'un facteur 0,25 le signal à 400 nm, et d'un facteur 0,5 le signal à 500 nm. On enregistre donc dans à 400 nm un signal de 0,25 x 30 = 7,5 et à 500 nm, un signal de 0,50 x 40 = 20. Le ratio apparent est de 7,5 / 20 = 0,375. Ce n'est pas du tout le résultat attendu ! Si on l’exploite tel quel, nous faisons une très grosse erreur en annonçant un résultat astrophysique erroné.

Supposons à présent que le produit (catégorie 1 x catégorie 2) = (transmission atmosphérique x réponse instrumentale) ai été évalué (nous allons voir comment ci-après). En valeurs relatives le résultat de ce produit vaut ici à 0,5 à 400 nm et  1,0 à 500 nm.

Pour restituer le vrai signal relatif de l'étoile, il suffit d'inverser numériquement l’atténuation en divisant le signal apparent observé par le rendement global spectral, soit ici,

- à 400 nm : 7,5 / 0,5 = 15
- à 500 nm : 20 / 1,0 = 20

Si nous faisons le rapport de ces deux valeurs rectifiées nous avons 15 / 20 = 0,75. Nous venons de trouver le vrai rapport d'intensité du flux stellaire entre 400 nm et 500 nm.

Pour résumé, on trouve le profil vrai de l'étoile appliquant la formule :

          (1)

Les termes en dénominateur de cette équation peuvent être trouvés à partir de deux méthodes.

La première méthode est différentielle. Elle permet d'évaluer en une fois le produit global (catégorie 1) x (catégorie 2).

La seconde méthode est photométrique. Les coefficients (catégorie 1)  et (catégorie 2) peuvent être séparés l’un et l’autre.

Je vais décrire successivement ces deux méthodes et dégager leurs avantages et défauts respectifs.
 

2. La méthode différentielle

On s'intéresse à l'étude d'une étoile, que l'on va appeler la cible. L'idée de la technique différentielle est d'observer au voisinage immédiat de cette cible une étoile dont on connaît le contenu spectral hors atmosphère. Cette caractéristique lui confère le rang d'étoile de référence. Il existe des catalogues spectrophotométriques où de tels objets sont regroupés. C'est le cas de la base de données MILES, reprise dans le logiciel ISIS. Cette intégration dans le logiciel permet d'extraire le profil hors atmosphère d'une étoile du catalogue pour un usage immédiat.

L’hypothèse sur laquelle repose la méthode est que l'étoile de référence est suffisamment proche angulairement de l'étoile cible que l'atténuation produite par l'atmosphère soit identiques pour les deux objets. Suivant la précision recherchée et la hauteur des objets au-dessus de l'horizon, l'écart maximal angulaire tolérable sera de quelques degrés à d'une dizaine de degrés. La séparation peut même être plus forte, mais à condition qu’elles les deux objets se situent sur un cercle approximativement parallèle à l'horizon. L'idée forte est que l'épaisseur d'air traversée, la masse d'air, soit identique pour les deux objets.

Pour montrer la mise en œuvre je vais m’appuyer sur une observation réelle de l’étoile de référence HD192640 (elle fait partie de la base MILES). Le spectrographe utilisé est un Alpy 600 monté au foyer f/4 d'un télescope de 200 mm de diamètre. On a pris 12 spectres successivement, avec un temps de pose de 60 secondes pour chacun.

Ces 12 images spectrales sont traitées avec le logiciel ISIS de manière classique, à ceci près qu’au départ la réponse instrumentale et la transmission atmosphérique ne sont pas connues. C’est justement  l’étude de ces 12 spectres de l’étoile de référence qui va nous permettre d’évaluer ces termes atténuateurs du flux stellaire.

La séquence à traiter est nommée hd192640b-1, hd192640b-2, ..., hd192640b-12. Voici comment est rempli l'onglet "Général" ISIS pour la circonstance :

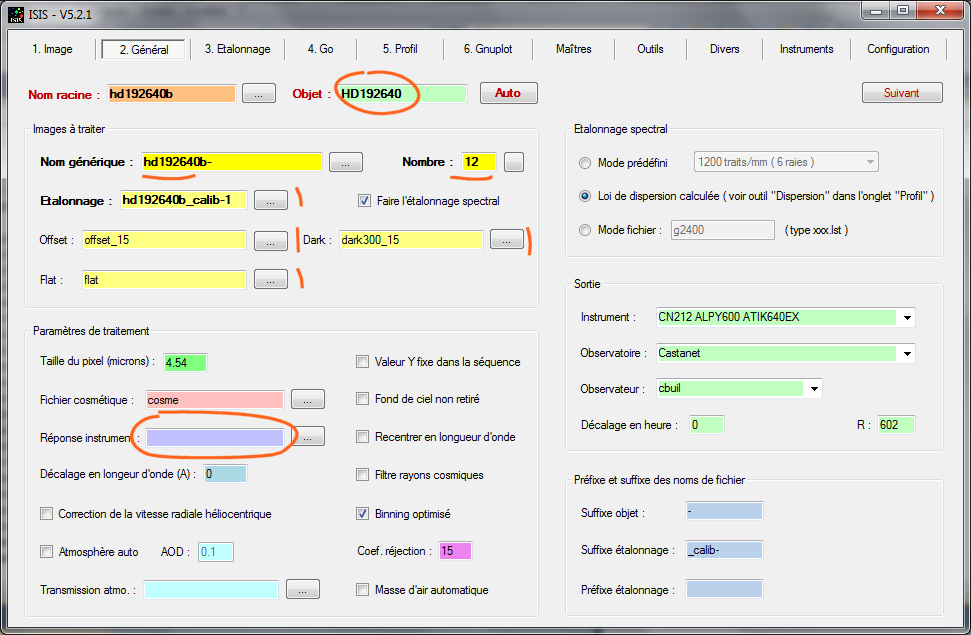
Notez que le champ "Réponse instrument" est laissé vierge. C'est bien cette fonction que l'on cherche à évaluer.

Plusieurs documents de la documentation de ISIS expliquent par le détails comment remplir l'onglet "Général" et la signification des différents champs de paramètres. En particulier :

- Le tutorial du spectrographe Alpy 600, qui s'appui du reste sur le traitement complet de cette même étoile HD192640. Cliquer ici.

- Le tutorial du spectrographe LISA (la méthode de traitement des spectres Alpy 600 et LISA est très voisine). Cliquer ici.

Voici le spectre de HD192640 après le traitement des 12 images en suivant les directives indiqués dans l'onglet "Général" :

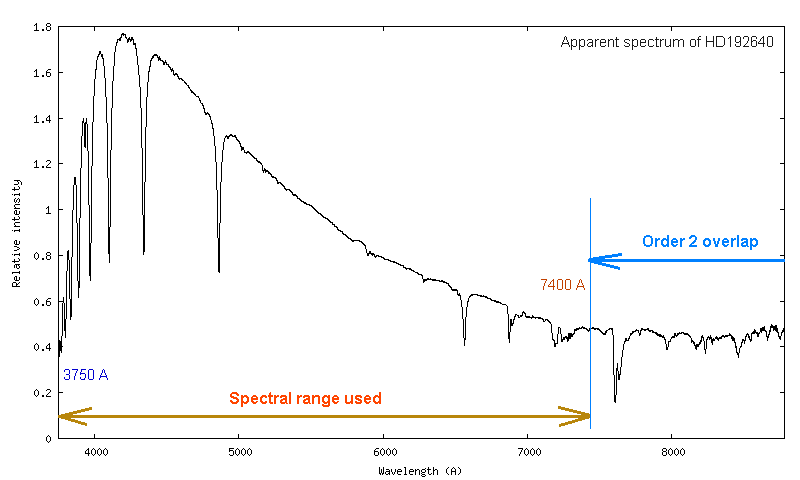
Comme cela a été souligné en introduction, l'allure du spectre restitué par la chaîne instrumentale est distordue par des atténuations de catégorie 1 et 2 (atmosphère et instrument).

Note pour les utilisateurs du spectrographe Alpy 600 : le spectre s'étend très loin dans le rouge profond, jusqu'à 8790 A dans l'exemple. La raison vient de l'usage d'un très grand capteur (celui qui équipe la caméra Atik 460 EX). En outre, le filtre de coupure IR n'est pas utilisé dans cette configuration. Au-delà de 7400 A environ, il s'avère que le recouvrement de l'ordre 2 devient sensible. Le spectre n'est donc pas utilisable au-dessus de cette longueur (à moins d'insérer un filtre d'ordre passe-haut, ce qui n'est pas le cas ici).

Voici le spectre de HD192640 extrait de la base de données MILES – c’est le spectre effectif de l'asre tel qu'il pourrait être vu en dehors de l’atmosphère terrestre avec un instrument spectralement neutre :

Ce spectre est plus résolue que celui produit par le specrographe Alpy 600. Une bonne idée est d'amener la résolution du spectre MILES à celle de Alpy 600 (soit un pouvoir de résolution voisin de R=600). Voici comment procéder sous ISIS :

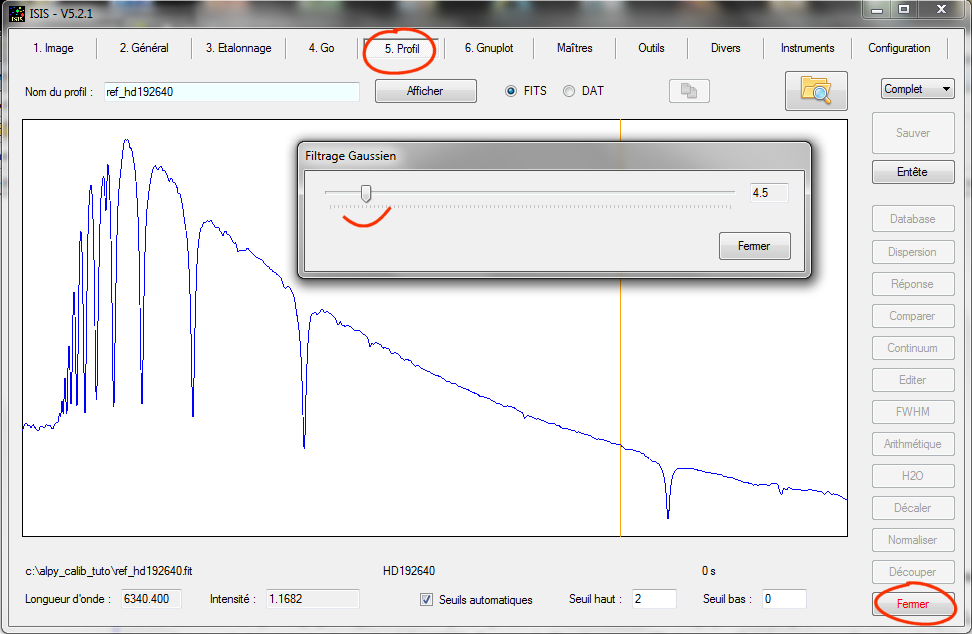
et le résultat, que l'on sauvegarde dans le répertoire de travail sous la forme d'un fichier profil nommé ici ref_hd192640  (le nom adopté est abritraire, mais il indique bien de quoi il s'agit).

On obtient la courbe spectrale de rendement global (incluant la réponse intrumentale et l'extinction atmophérique) en divisant le profil observé de HD192640 par le profil MILES, "ref_hd192640". Voici une manière de faire sous ISIS à partir de l'outil "Comparer" :

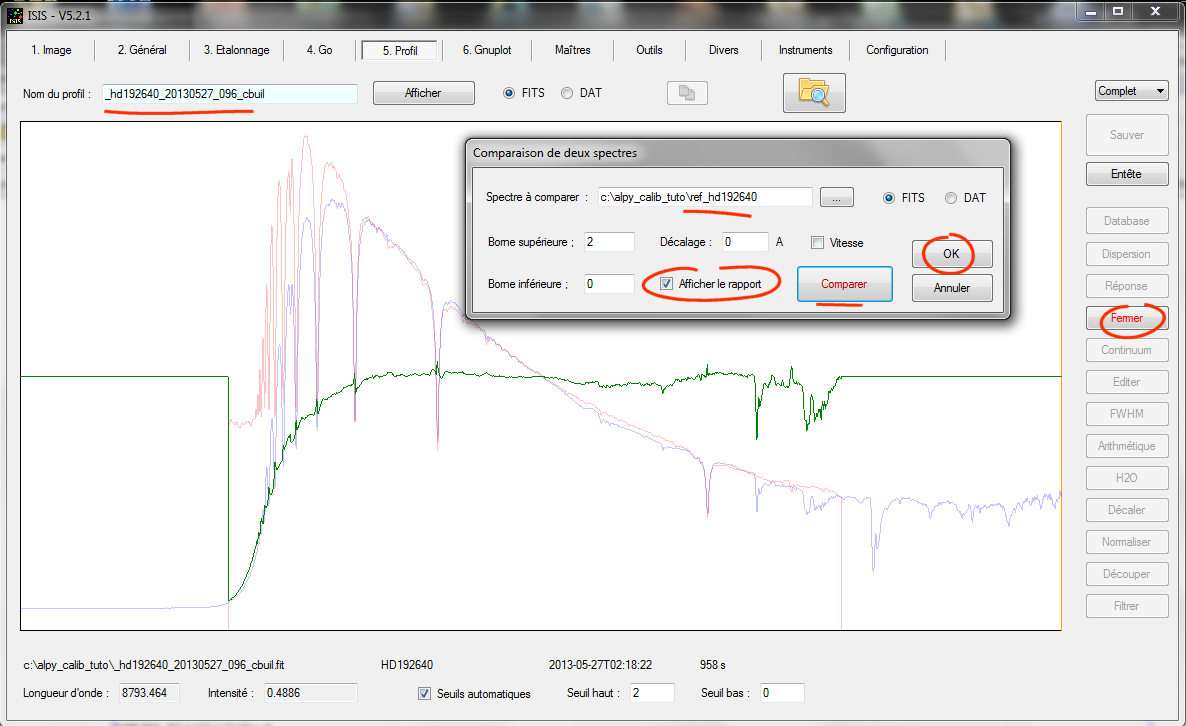
Dans cette copie d'écran, en bleu le profil observé, en rouge le profil attendu hors atmosphère et hors instrument (profil MILES), en vert le rapport des deux, c'est-à-dire, le rendement instrumental (incluant donc l'atténuation spectrale de l'instrument et de l'atmosphère).

Après le gommage des quelques aspérités au niveau des raies spectrales Balmer (ce sont des artefacts de calcul et qui n'ont rien avoir avec la réponse) - voir le tutorial LISA en particulier, et après détourage, on obtient le rendement instrumental global recherché (on nomme ce fichier profil rendement dans le répertoire de travail, tout simplement) :

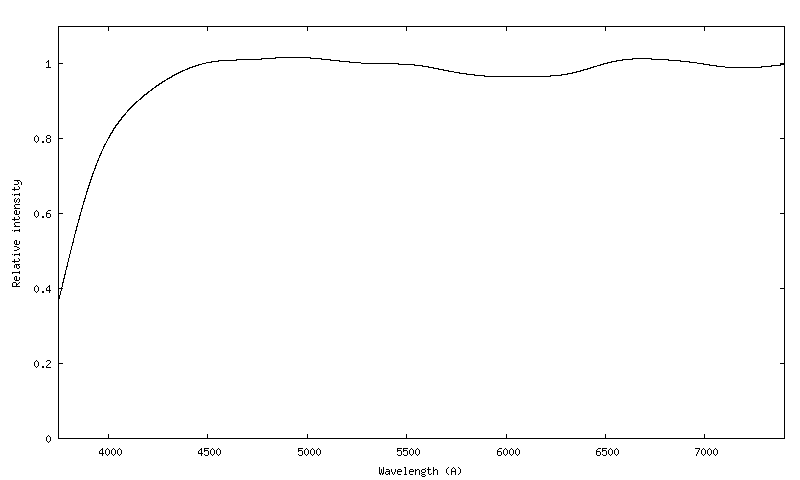
Le calcul réalisé s'écrit :

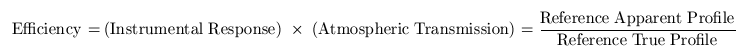      (2)

Il est important de noter que cette courbe est la traduction du produit (transmission atmosphérique) x (réponse instrumentale) en fonction de la longueur d'onde. On l'appelle rendement ou efficacité du système (system efficiency en anglais). Si notre étoile avait été observée à une hauteur différente au-dessus de l'horizon, la forme de la courbe serait différente, car le terme (transmission atmosphérique) n'a plus les mêmes valeurs. Il ne s'agit donc pas ici d'une "réponse instrumentale" alors que souvent on attribue ce nom au résultat de ce calcul. C'est un sujet de controverse qui peut rendre perplexe celui qui n'est pas prévenu : d'une nuit à l'autre, d'une heure à l'autre, la "réponse" de l'instrument semble ainsi changer, ce qui est déroutant - comme si l'instrument était instable. C'est en fait la transmission atmosphérique qui est ici la variable. Ce que nous appelons ici "réponse instrumentale" peut donc être de qualifié de pseudo réponse.

Même ISIS contribue à sa manière à entretenir cette ambiguïté comme on va le voir...

Exploitons la courbe de rendement système juste trouvé pour un nouveau traitement du le spectre de HD192640. La seule différence par rapport au traitement précédent est le contenu du champ "Réponse instrument" dans l'onglet "Général" :

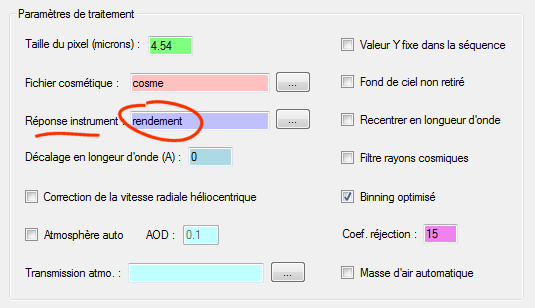
Ici il y a un contresens :  on indique dans le champ "Réponse instrument" le fichier rendement,  qui n'est nullement la réponse instrumentale puisqu'on y trouve aussi l'influence de la transmission atmosphérique. A ce stade, l'intitulé "Réponse instrument" dans l'interface de ISIS est donc particulièrement mal à propos (mais il sera justifié plus loin....). Il faut essayer de passer outre, et surtout bien comprendre ce qu'est le fichier rendement, c'est-à-dire le produit  (transmission atmosphérique) x (réponse instrument).

Une fois le champ "Réponse instrument" rempli,  ne rien changer d'autre et aller directement à l'onglet "Go", puis cliquer le bouton "Go". Voici le résultat :

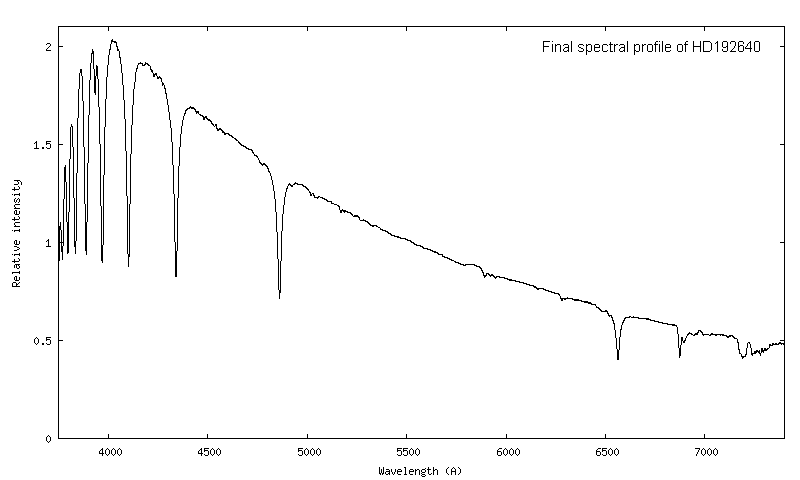
Le calcul fait par ISIS est celui décrit par l'équation 1. Le profil trouvé est bien celui que l'on verrait avec un instrument parfaitement neutre spectralement et placé en dehors de l'atmosphère.

Note : ce n'est pas tout à fait exact en réalité... en particulier autour de la raie Halpha et pour des longueurs d'onde plus grande que 6700 A, l'absorption par les bandes telluriques O2 et H2O sont encore présentes, car a contrario, absentes du profil MILES.

L'intérêt de tout ce travail préparatoire (évaluation du fichier rendement) est de permettre de calculer le vrai spectre de l'étoile cible, voisine angulairement de l'étoile de référence. Par exemple ici, une petite séquence de l'étoile RR Lyrae, proche de HD192640 (ce n'est pas un hasard !) et prise approximativement au même moment. Voici la première image de cinq acquises (le temps de pose est de 300 secondes) :

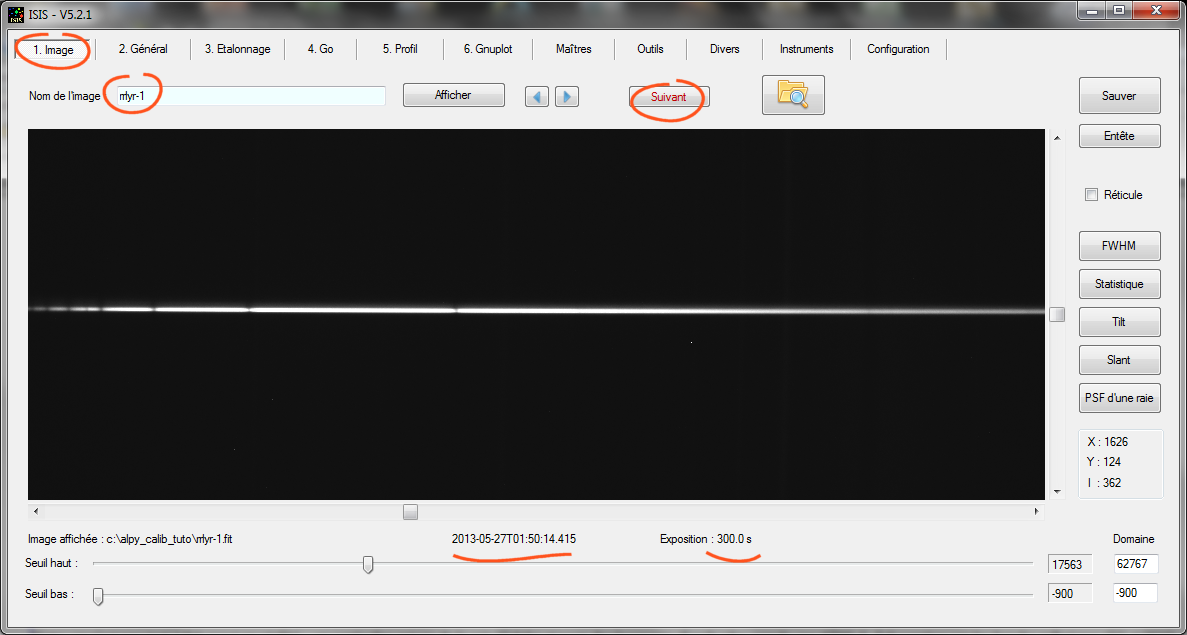
Voici l'onglet "Général" rempli pour ce traitement :

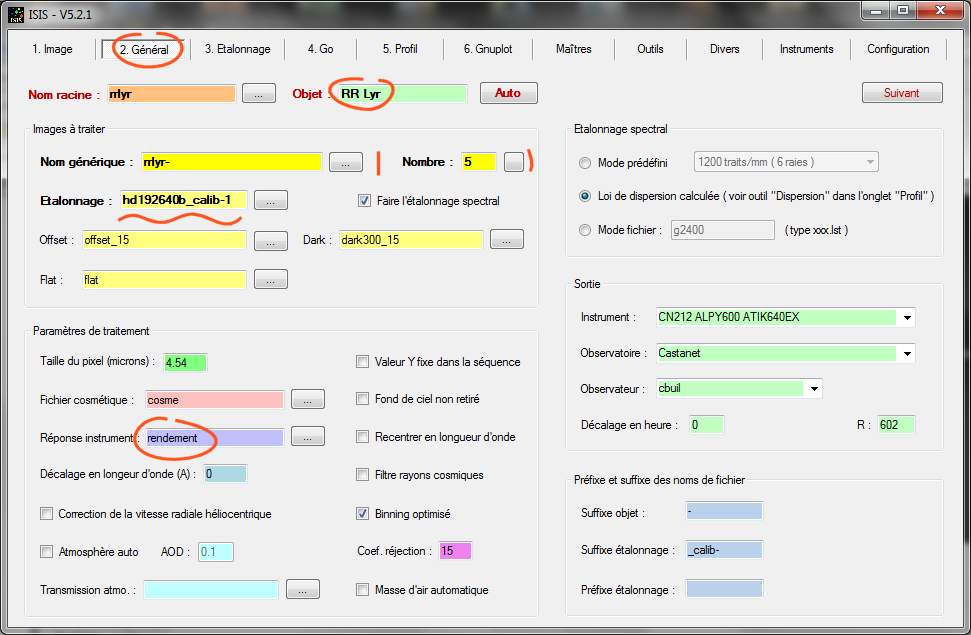
Remarquer que le champ "Réponse instrument" est bien renseigné. Noter aussi que le fichier d'étalonnage en longueur d'onde est le même que celui utilisé pour traiter HD192640. Le spectrographe Alpy 600 est si stable mécaniquement que l'on peut se permettre ce genre de facilité.

Le spectre vrai de RR Lyrae (hors atmosphère) ainsi calculé est (l'étoile est ici à son maximum de brillance) :

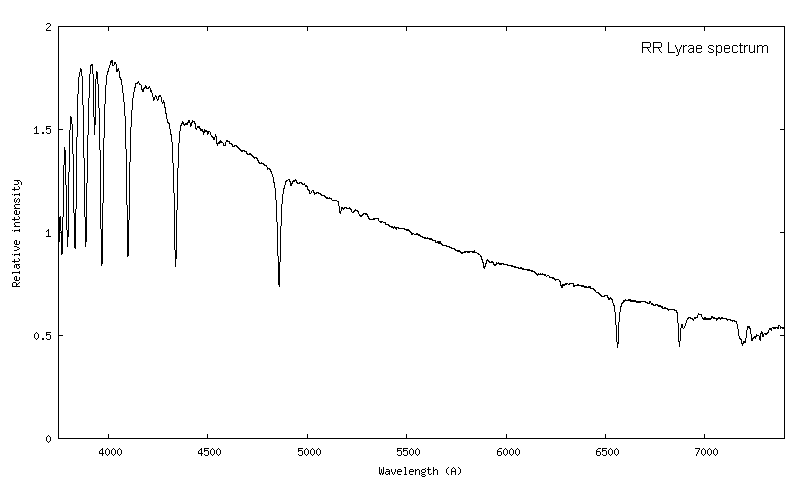
L'ensemble des opérations réalisées dans la méthode différentielle peut ce résumé à l'équation :

          (2')

On peut noter que grace au deuxième terme de cette équation : (Profil Observé de la Cible) / (Profil Observé de la Référence), l'impact de la transmission atmosphérique, mais aussi celui de la réponse instrumentale disparait. En effet, par définition, la transmission atmosphérique et la réponse étant identiques même pour ces deux observations, leur effet s'annule dans le rapport. C'est la clef de la méthode différentielle : l'état de l'atmosphère n'est pas critique.

On remarque au passage qu'il n'est même pas utile de calculer le rendement instrumental puisqu'il est le même au numérateur et au dénominateur. Il est cependant recommandé de procéder à cette évaluation afin que les profils individuel prétraités (cible et référence) ressemblent tout de même à ceux de spectres stellaires. C'est plus rassurant et cela permet de faire des vérifications.

L'intérêt de la méthode différentielle est d'être assez expéditive et simple. En une prise de spectre on calcule les distorsions spectrales associées à la transmission atmosphérique et à l'instrument lui-même. Cependant, il faut systématiquelent coupler à l'observation d'un objet cible donné une observation équivalente sur une étoile de réference voisine à peu près au même moment, si on veut bien sur réaliser un travail précis. C'est assez long et fastidieux.  On note que la réponse instrumentale (distincte de la transmission atmosphérique) n'est jamais extraite en tant que telle.
 

3. La méthode photométrique

La méthode nécessite d'observer l'étoile de référence à deux masses d'air distinctes. Cet écart de masse d'air donne accès à la transmission atmosphérique réelle. Dans un second temps, nous pouvons calculer la réponse instrumentale relative. Au terme du calcul, les deux termes du dénominateur de l'équation sont donc évalués.

L'évaluation de la transmission atmosphérique est d'autant plus précise que l'écart de masse d'air est grand. La difficulté est donc qu'entre les deux observations de l'étoile de référence il peut s'écouler une durée longue (le temps que l'étoile s'élève ou descende relativement à l'horizon). La technique ne fonctionne donc que lorsque la nuit stable sur le plan météorologique, on dit photométrique ou quasi photométrique.

La méthode mathématique pour extraire la transmission atmosphérique à partir de deux observations du même objet à des masses d'air différentes est décrite dans la page: https://buil.astrosurf.com/atmosphere/transmission.htm

Je vais illustrer par un exemple concret. On dispose de deux séquences d'observation de l'étoile HD192640 :

- Une première séquence "a" de 13 images posées chacune 60 secondes autour de la date du 26,886 / 05 / 2013 (milieu de l'observation) - HD192640a-1, ... HD192640a-13

- Une seconde séquence "b" de 12 images posées chacune 60 secondes autour de la date du 27,102 / 05 / 2013 (milieu de l'observation) - HD192640b-1, ... HD192640b-12

L'écart de temps entre ces deux observations est de 5 heures. Une ou deux observations intermédaires de cette étoiles sont faites à titre de contrôle dans cette longueur période.

Ces séquences sont traitées de manière classique (avec leur étalonnage spectral associé), mais sans rien indiquer pour la "Réponse instrument". Par exemple pour la première séquence :

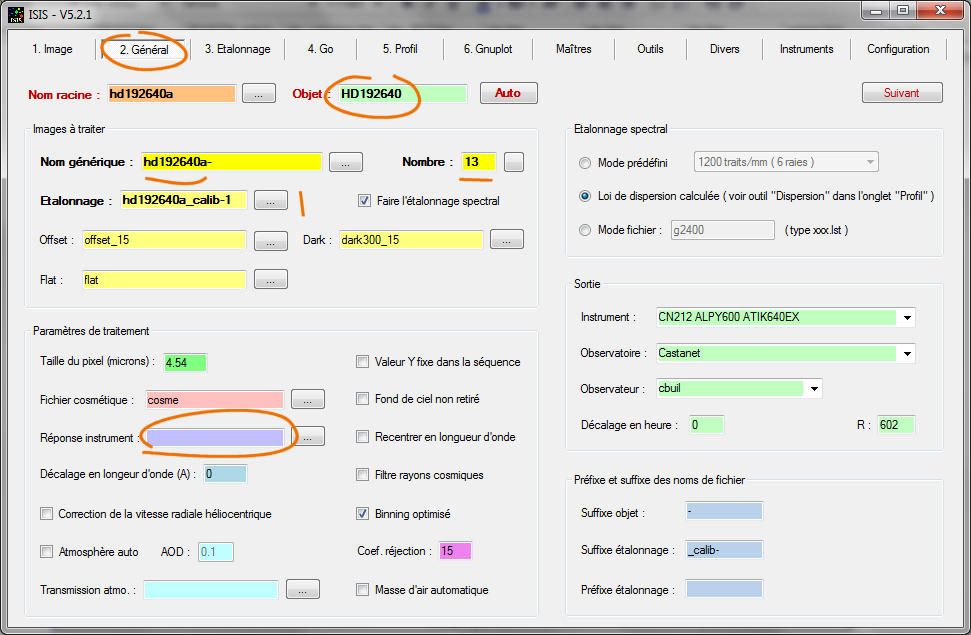
Avant de lancer le traitement, il faut faire une petite manœuvre préalable. Nous souhaitons en effet obtenir des profils spectraux en pas codeur (ou unité de pas analogique, ADU en anglais), alors que de manière naturelle ISIS normalise le profil à l'unité dans une plage de longueur d'onde que vous définissez dans l'onglet "Configuration". Par exemple, pour cette étude, qui concerne le suivi de l'étoile RR Lyrae, j'ai choisi une zone de calcul de la norme comprise entre 5450 A et 5600 A. L'astuce pour forcer ISIS à ne pas normaliser est de rentrer des valeurs nulles pour les bornes de normalisation :

Lancer l'extraction du profil depuis l'onglet "Go". Noter que ISIS indique la date du milieu de l'observation au terme du traitement. Relevez cette information :

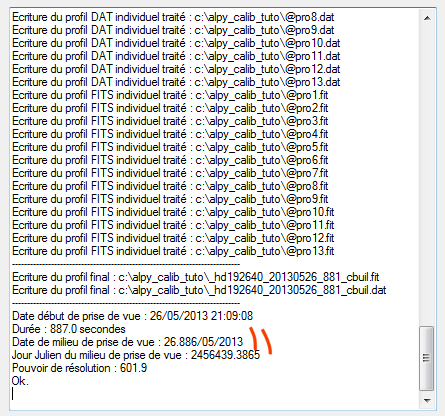
Attention ici. L'intensité dans les deux profils calculés n'est pas directement comparable, car si les temps de pose individuels des images sont identiques, en revanche, la première séquence comporte 13 images et la seconde 12 seulement. Donc les intensités en pas codeur ne sont pas cohérentes. Nous allons ramener l'intensité du profil "a" (le premier) à ce qu'il serait si nous avions travaillé avec 12 images. Le profil de la première séquence doit donc être multiplié par le coefficient 12 / 13 = 0.923.

Pour cela, chargez ce profil en mémoire, puis utilisez l'outil "Arithmétique" :

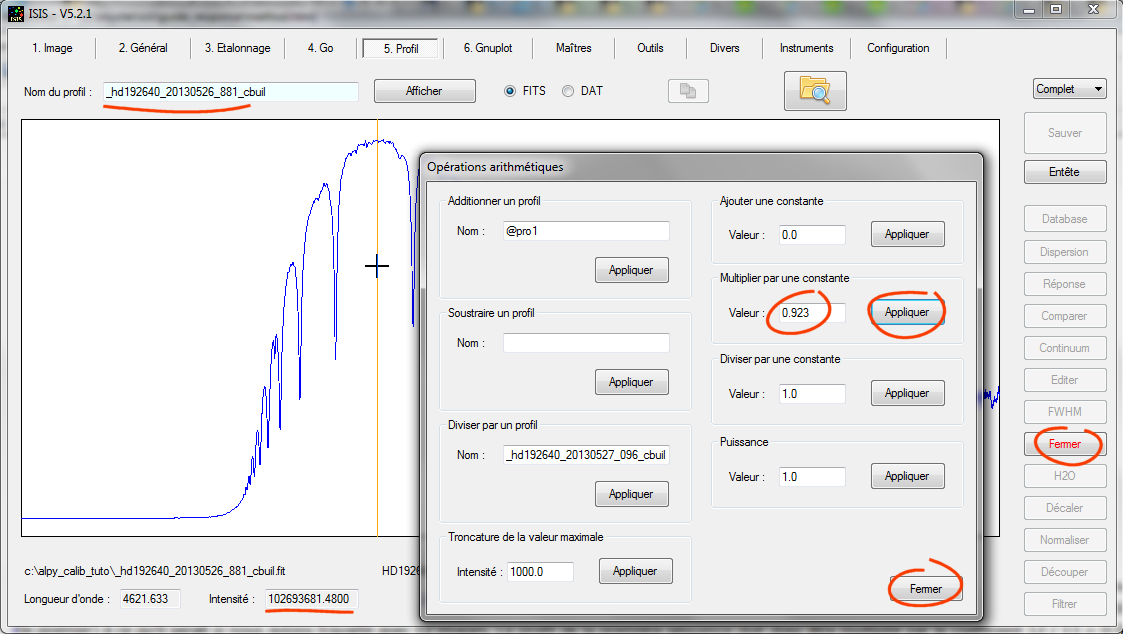
Une fois la multiplication appliquée, fermer la boite dialogue, puis sauvegardez le profil modifié en écrasant le précédent.  Par exemple :

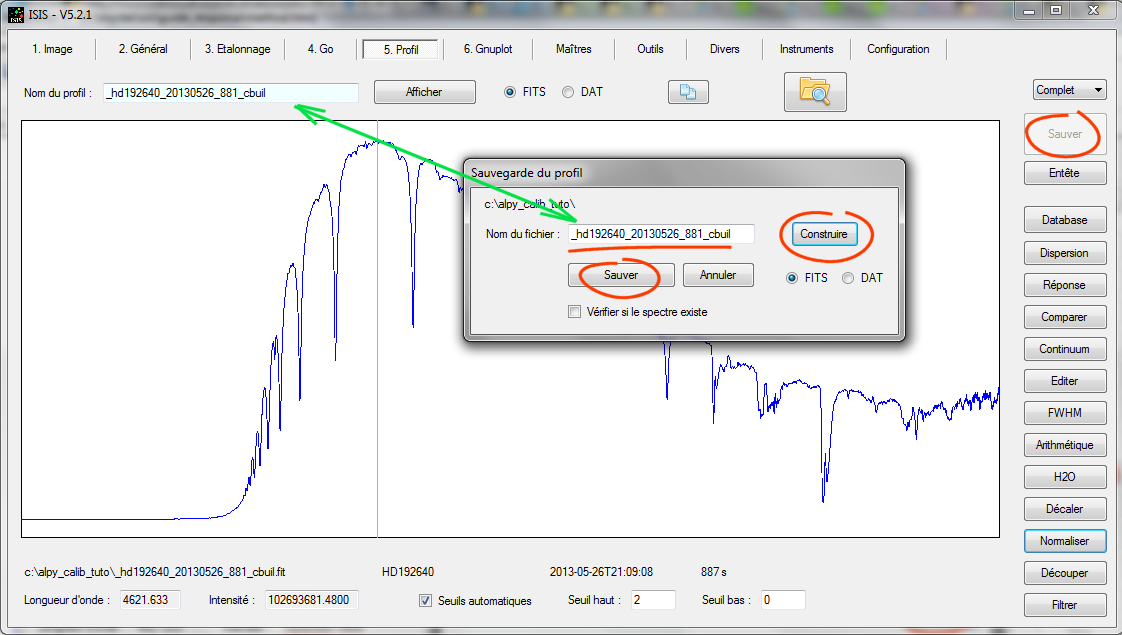
Voici l'aspect des deux profils affichés sur le même graphe :

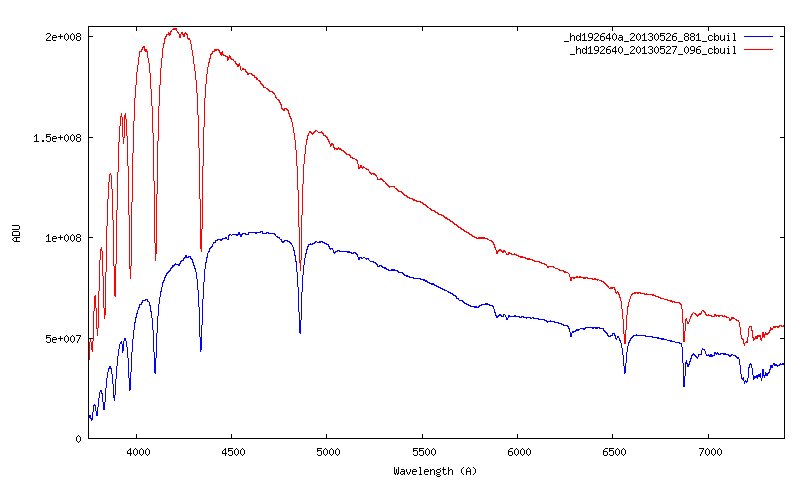
L'écart est considérable alors qu'il s'agit de la même étoile. La seule différence est que le profil bleu est obtenue alors que l'étoile est assez basse sur l'horizon, alors que la courbe rouge est obtenue alors que l'étoile est proche du zénith. L'intégrité des données acquises est vraiment fortement affectée par l'atmosphère. Il toujours important de ce rappeler que depuis le sol, on observe au travers d'un fitre spectral particulièrement redoutable et variable !

Nous avons tout pour calculer le rapport des deux termes de l'équation (rappel T est la transmission de l'atmophère au zénith) :

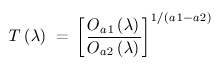              (3)

Dans notre exemple, le profil en numérateur est celui issu de la séquence "a", alors le profil en dénominateur vient de la séquence "b".

A partir de l'outil "Arithmétique", diviser le premier profil (séquence "a") par le second profil (séquence "b") :

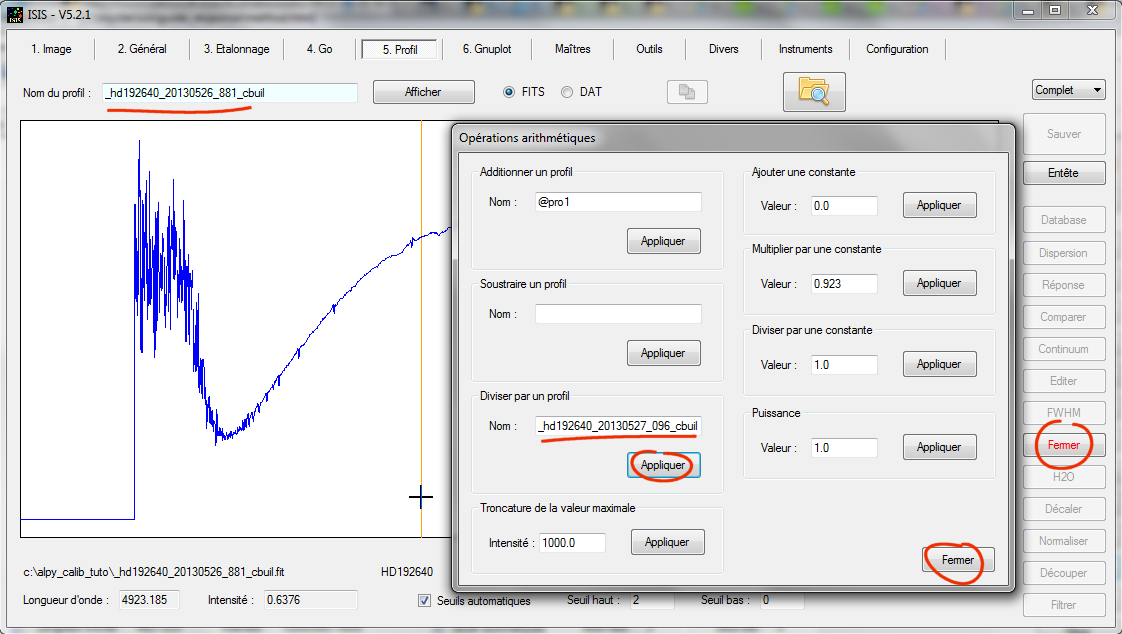
Voici le ratio trouvé sous forme graphique :

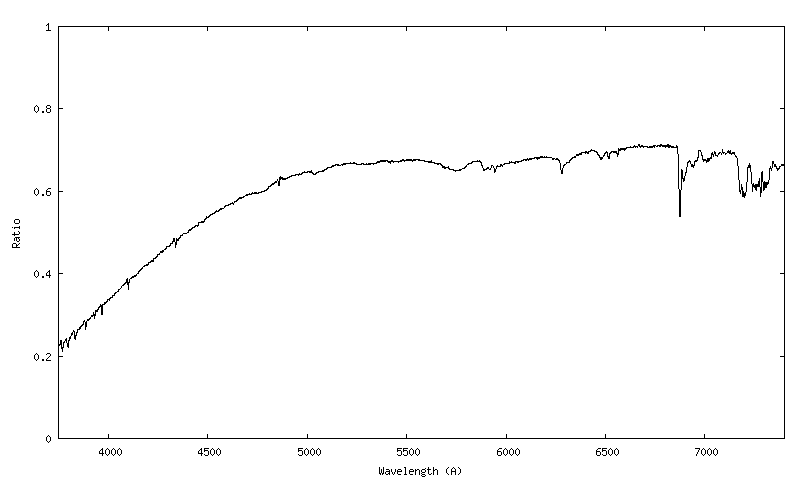
On va lisser localement (et délicatement) les petites aspérités résiduelles au niveau des raies de Balmer dans le bleu pour parfaire le calcul de la transmission atmosphérique. On utilise pour cela l'outil "Continuum" (d'une manière générale, il est extrêmement utile de bien maîtriser cette fonction !). Voici le ratio nettoyé :

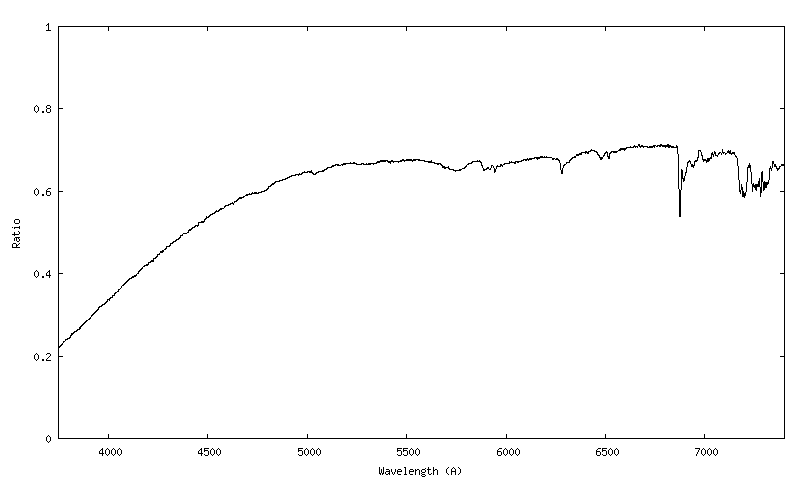
Cette courbe n'est pas encore la transmission atmosphérique absolue (pour une masse d'air unitaire). D'après la formule (3), il reste à l'élever à la puissance 1/(a1 - a2), avec a1 et a2 respectivement les masses d'air traversées lors de la première observation (séquence "a") et lors de la seconde observation (séquence "b").

Pour trouver les masses d'air, ouvrir l'onglet "Divers", puis l'onglet "Vitesse héliocentrique". Fournir la date d'observation et les coordonnées équatoriales de l'objet (ici nous avons fait une recherche Simbad à partir du numéro catalogue HD) :

On constate que lors de la première observation, HD192640 se trouve 19,03° au-dessus de l'horizon. La masse d'air correspondante est a1 = 3,044.

Note : attention, penser à bien mettre à jour les coordonnées géographiques de votre observatoire dans l'onglet "Configuration".

Cinq heures après, la position de l'étoile dans le ciel local est :

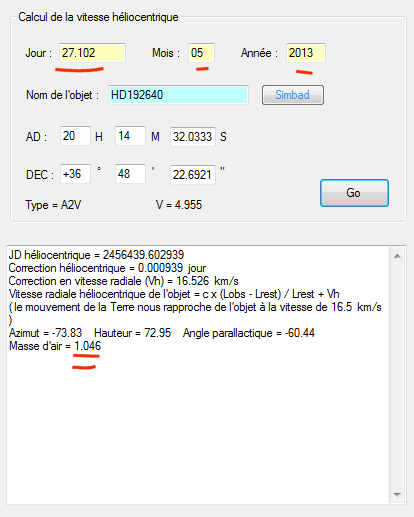
Soit a2 = 1,046.

On calcule 1/(a1 - a2) = 0,5005. Pour élever à la puissance notre ratio, il faut encore passer par l'outil "Arithmétique" :

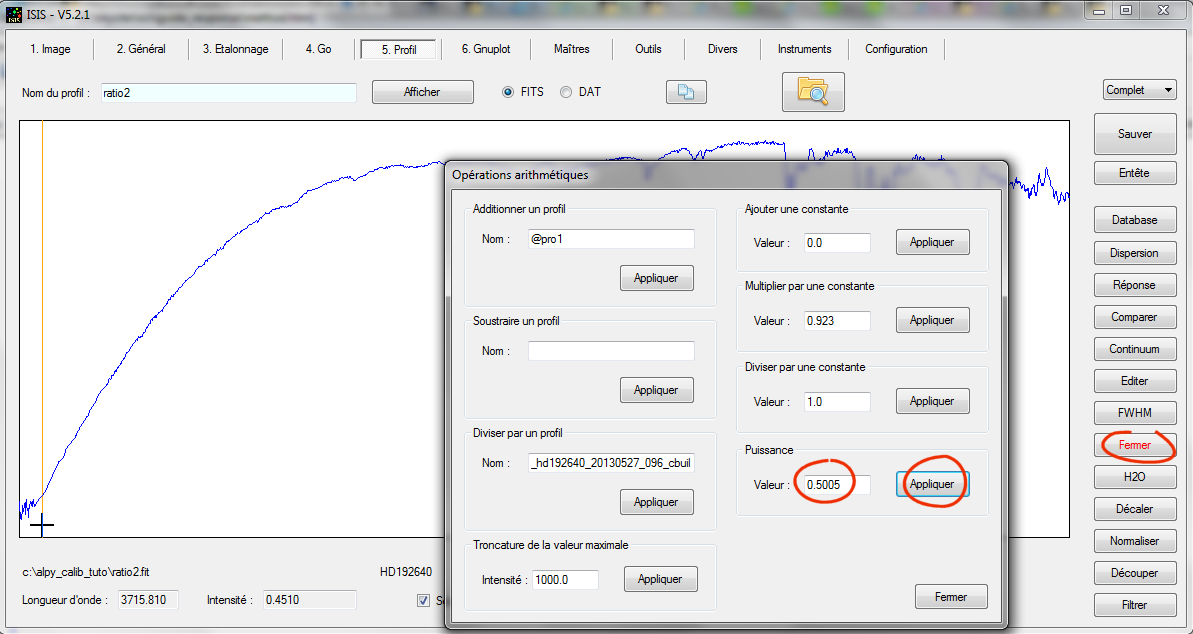
On sauvegarde le résultat dans le répertoire de travail sous le nom trans_atmo (par exemple) :

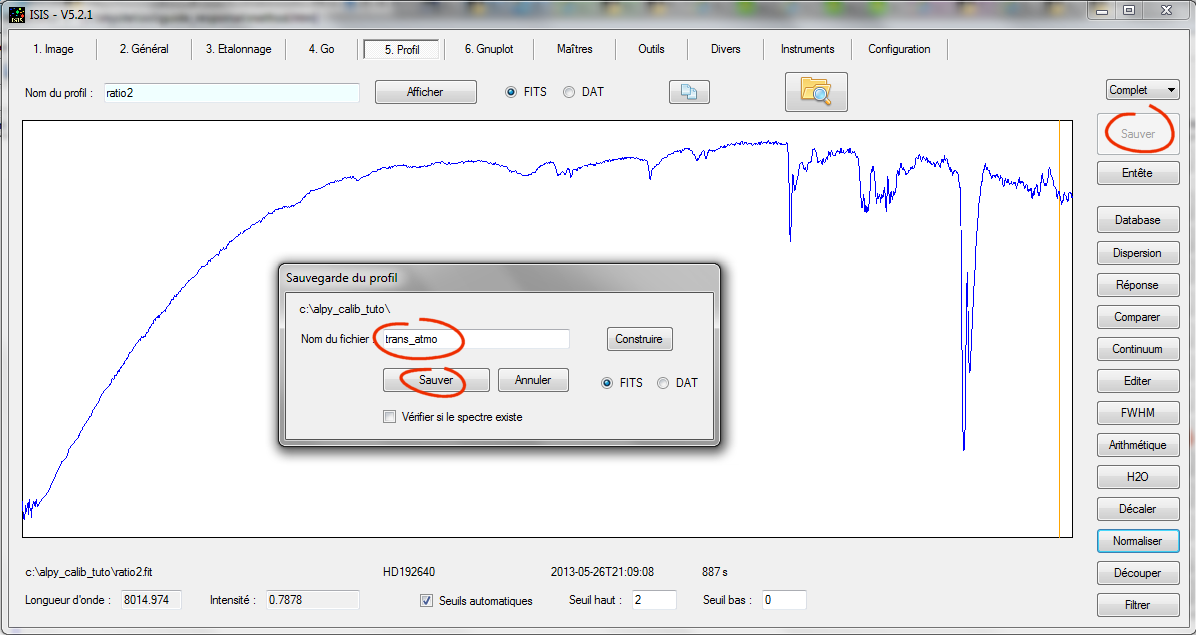
La courbe "trans_atmo" est la vraie transmission de l'atmosphère au zénith pour la nuit d'observation considérée (soit pour une masse d'air unitaire, a = 1) :

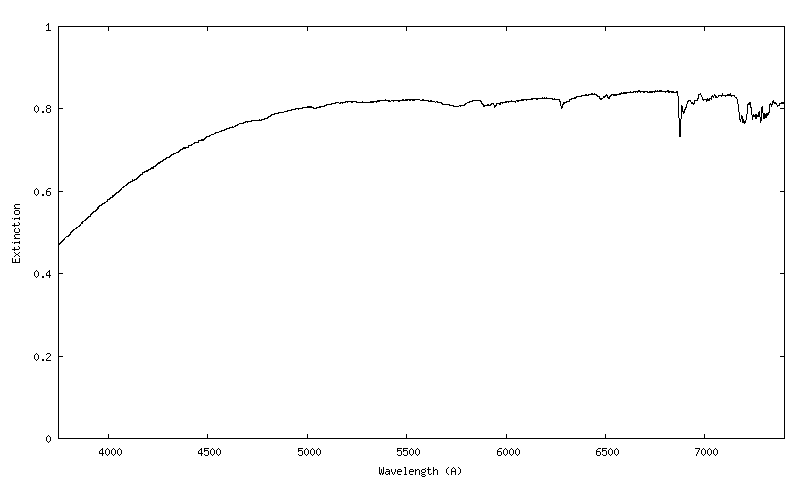
On remarque que le flux stellaire est atténué de 20% dans le rouge et dans le vert depuis mon observatoire urbain de Castanet-Tolosan. L'extinction est de 53% environ vers 4750 A.

Nous disposons à présent du premier terme du produit dans le dénominateur de l'équation 1. Il reste à trouver la réponse instrumentale proprement dite.

La technique consiste à calculer le profil de l'étoile observé (par exemple, celui de la séquence "b") tel qu'il serait vu depuis l'espace, c'est-à-dire en l'absence de l'atmosphère terrestre. On divise pour cela le profil apparent par la transmission atmosphérique calculée pour la masse d'air traversée par la lumière de l'étoile, ce qui donne

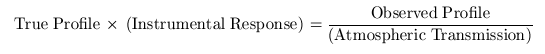          (4)

Il suffit ensuite de diviser le résultat de cette opération par le profil vrai de l'étoile de référence pour trouver la réponse instrumentale.

Dans l'équation 4, la transmission atmosphérique est associée à la masse d'air a de l'étoile. La formule suivante permet de trouver cette transmission :

            (5)

ISIS peut faire le calcul correspondant à l'équation 4 automatiquement. Voici comment est organisé l'onglet "Général" pour cela :

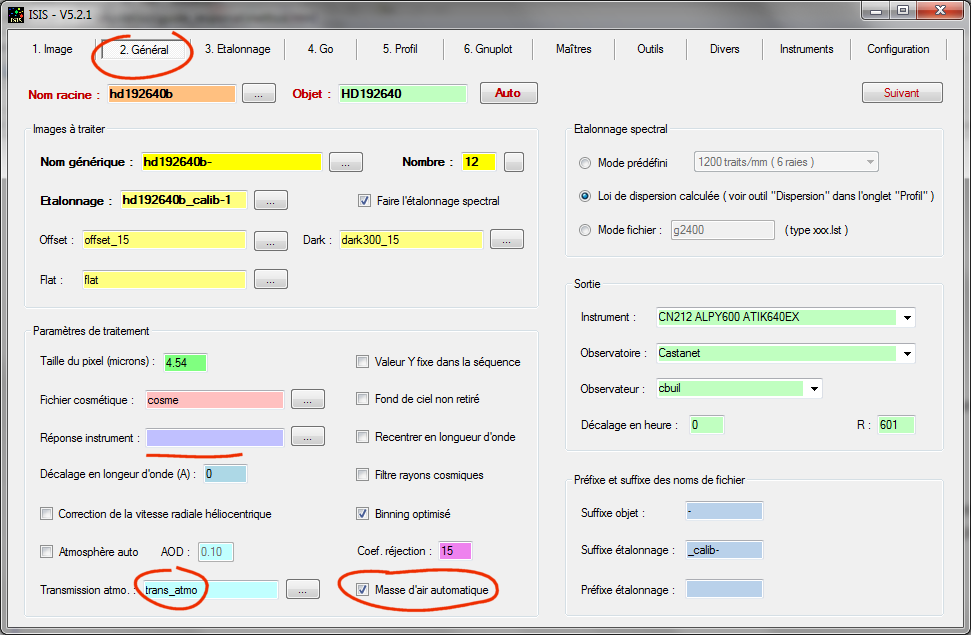
On donne le nom du fichier de transmission atmosphérique pour une masse d'air a = 1 (ici trans_atmo). On coche par ailleurs l'option "Masse d'air automatique", ce qui oblige ISIS à calculer la masse d'air automatiquement pour l'étoile HD192640 au milieu de sa période d'observation. ISIS calcule ensuite la transmission atmosphérique correspondante (équation 5) et réalise ensuite la division (équation 4).

Note : ISIS interroge ici automatiquement Simbad pour trouver les coordonnées équatoriales de l'objet. Si vous n'êtes pas connectés à Internet ou si le nom que vous donnez à l'objet (champ "Objet") n'est pas résolu pas Simbad, la procédure échoue. Cependant, ISIS vous demande à ce stade s'il peut continuer la calcul avec les coordonnées équatoriales inscrites dans l'onglet "Divers" / "Vitesse héliocentrique". Ceci vous permet d'extraire des spectres, même si vous n'êtes pas branché sur Internet.

Voici le résultat de l'opération décrite par l'équation 4 :

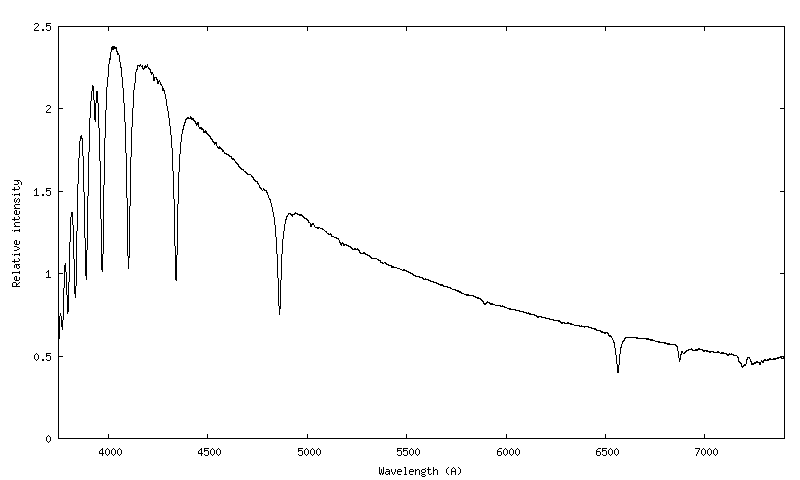
On rappelle qu'il s'agit du profil produit par un ensemble télescope + spectrographe exploité dans un observatoire qui orbite autour de la Terre. Ce profil est encore distordu par la réponse instrumentale. Comme le spectre attendu de l'étoile est connu, pour trouver la réponse instrumentale, il suffit de diviser ce profil par le spectre MILES. Vous pouvez utiliser l'outil "Comparer" pour cela, où encore réaliser une division directe à partir de l'outil "Arithmétique" :

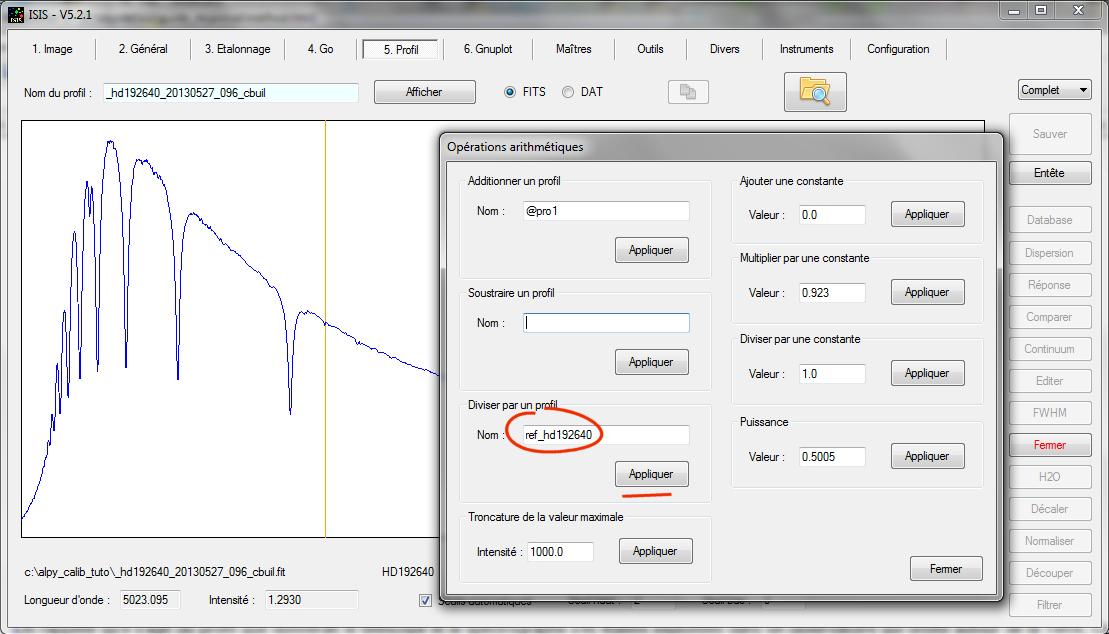
Le calcul réalisée est :

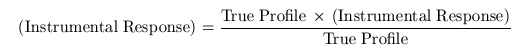        (6)

Voici enfin la vrai réponse instrumentale (terme de catégorie 2), trouvée avec l'équation 6,  après ellimination des résidus de raies de Balmer et de raies telluriques, puis détourage à la partie utile :

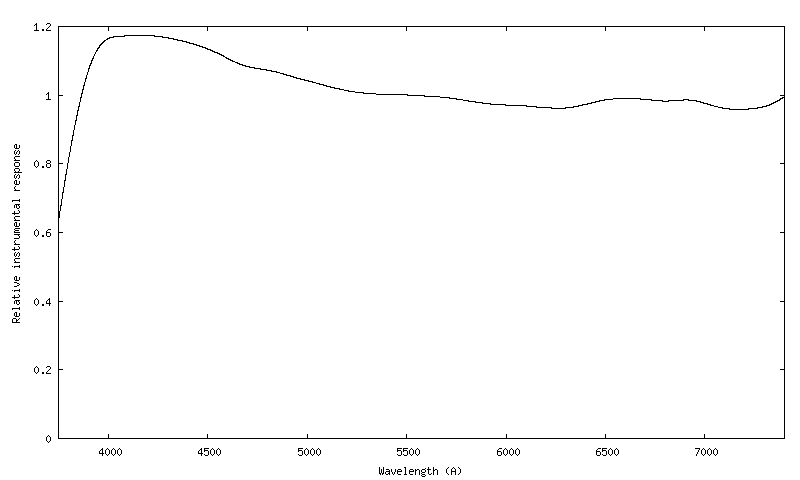
On a donné le nom reponse_inst à ce fichier. Vous pouvez adopter une tout autre nomination bien sûr. Cette courbe est une vraie constante de votre instrument, sa signature en quelque sorte. Elle est indépendante de la transmission atmosphérique, et en principe vous n'avez à l'évaluer qu'une seule fois. Il est sage cependant de l'actualiser régulièrement.

Voici à présent comment régler l'onglet "Général" pour extraire le profil spectral de toute étoile observée dans la nuit considérée :

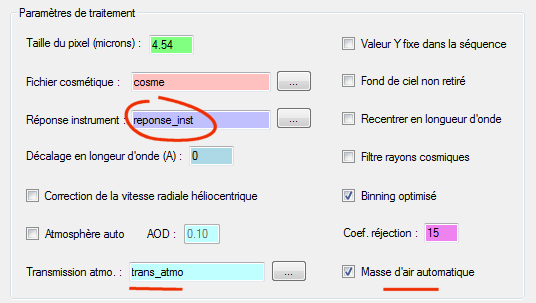
Cette fois, la signification du champ "Réponse instrument" n'est plus ambiguë. C'est bien la vraie réponse instrumentale que l'on fournit, bien distincte de la transmission atmosphérique. Cela justifie l'intitulé adopté dans l'interface de ISIS !

Voici le spectre final de HD192640 traité avec la méthode photométrique :

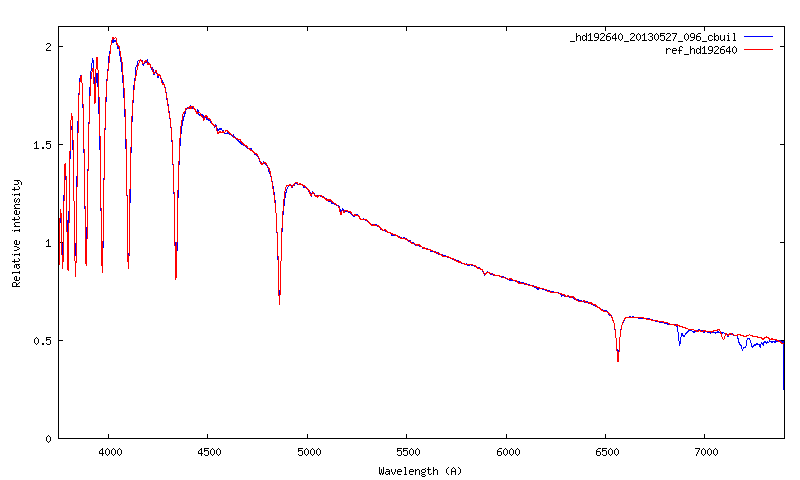
On notera au passage la très bonne qualité des résultats fournis par le spectrographe Alpy 600, y comprit jusque dans l'ultraviolet.

La méthode photométrique consomme au départ du temps d'observation pour trouver la transmission atmosphérique (prise de spectres d'une même étoile pour plusieurs masses d'air). Ce peut être un temps masqué entre l'observation de deux cibles, ce qui alors assez peu pénalisant.

Le gros avantage est qu'une fois la transmission atmosphérique calculée, vous pouvez entièrement vous consacré à vos cibles, sans vous soucier de jongler avec des étoiles de référence. C'est extrêmement confortable et efficace (j'ai peu apprécié la précision de la méthode). Cette façon de travailler est par exemple précieuse lorsqu’on fait le suivi sur un long temps et en permanence d'un objet tel que RR Lyrae : on ne quitte quasiment jamais la cible de vue !

Ci-après, l'onglet "Général" pour le traitement de l'étoile RR Lyrae. Au moins pour la nuit concernée, les fichiers reponse_inst et trans_atmo sont des constantes, quel que soit l'objet pointé, ce qui simplifie fortement le traitement (et l'acquisition des données en routine) :

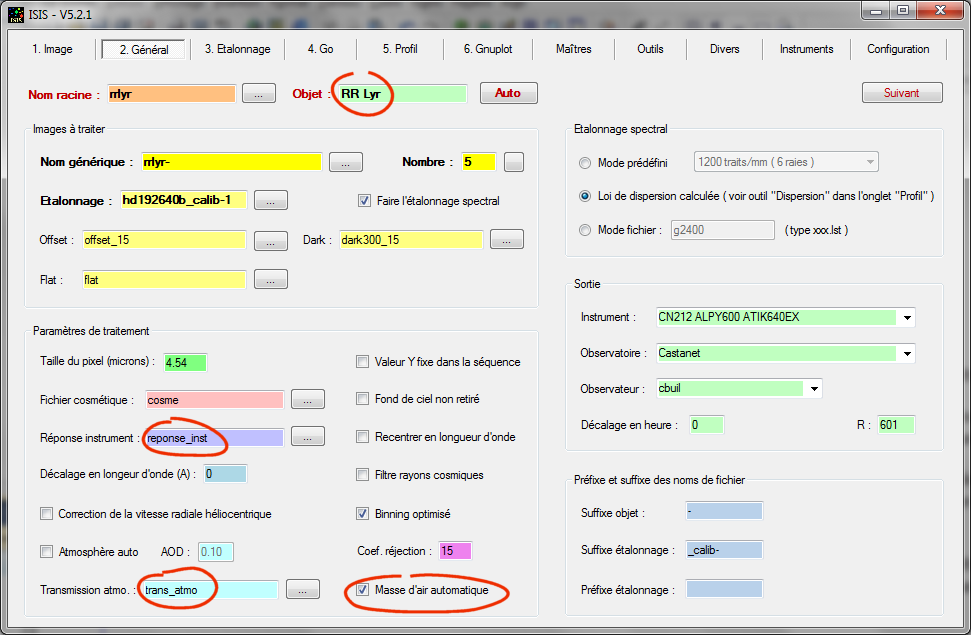
Au fur et à mesure que vous observez (de nuit en nuit), vous pouvez affiner la connaissance de la réponse instrumentale et aussi finir par établir une bibliothèque de transmission atmosphérique en fonction des conditions météo (hiver, été, ...). A partir d'un certain moment, il est presque possible de se passer d'observer des étoiles de références pour trouver le vrai continuum des étoiles.

Comme son nom l'indique, la méthode photométrique ne fonctionne que si la nuit est photométrique ou quasiment. Si tel n'est pas le cas, il faut se résigner à observer dans le mode différentiel.

On doit souligner aussi la critcité de la largeur de fente choisie en regard du seeing et de l'ampleur de la dispersion atmosphérique. La qualité du résultat dépend fortement de cette largeur. C'est un sujet important discuté sur cette page.
 

4. La transmission atmosphérique synthétique

ISIS peut calculer une transmission atmosphérique via un modèle numérique. Voici comment activer cette fonction depuis l'onglet "Général" :

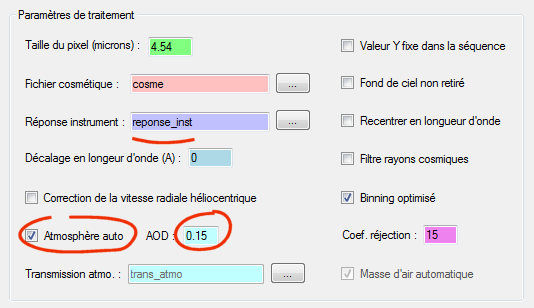
L'indice AOD est fonction de la quantité d'aérosol dans l'atmosphère. La valeur de 0,15 est la plus approchante des conditions d'observations, mais le résultat est assez décevant par rapport à une mesure réelle de la transmission en l'état de l'investigation :

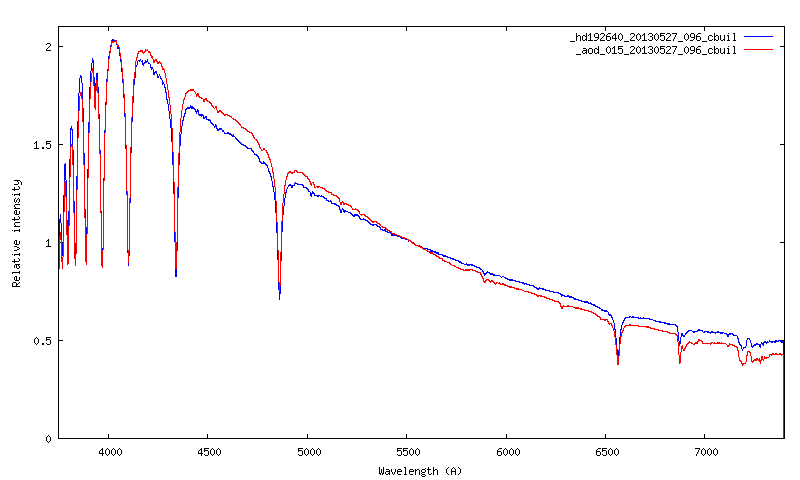
4. Quelques précautions

La température de couleur de la lampe tungstène (ou halogène) utilisée pour fabriquer l'image flat-field "colore" le profil spectral calculé. ISIS divise en effet les données brutes par l'image flat-field. L'explication tiens dans cette équation fondamentale :

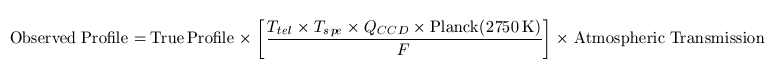        (8)

Elle exprime l'ensemble des termes qui modifient le profil vrai de l'objet observé lors du traitement avec ISIS :

- Ttel est la transmission optique spectrale du télescope ;

- Tspe est la transmission optique du spectrographe ;

- Qccd est le rendement quantique spectral du détecteur ;

- F est le signal mesuré de la lampe blanche d'étalonnage flat-field ;

- Planck(2750 K) est une courbe de Planck synthétique (calculée) pour un corps noir de 2750 K (cette température est paramètre interne de ISIS).

Si par exemple la lampe "blanche" flat-field est positionnée juste à l'avant de la fente d'entrée du specrographe (la situation du module d'étalonnage Alpy ou du spectrographe LISA, par exemple), on a

      (9)

et finalement

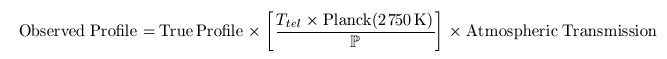        (10)

avec P, le spectre émis par la lampe flat-field d'étalonnage (un quasi profil de corps noir).

Le spectre continu de la lampe flat-field permet d'éliminer la contribution du détecteur CCD (pixel à pixel variation de réponse) et du spectrographe (vignetage). Ceci suppose que la distribution du flux flat-field et du flux cible est la même sur le détecteur, ce n'est pas toujours strictement le cas à cause de la manière d'éclairer la fente avec la lampe d'étalonnage, mais l'équation (10) demeure une bonne approximation (en particulier, la réponse pixel à pixel du CCD devient bien uniforme, ce qui justifie la correction flat-field).

Le but de la courbe de Planck calculée (Planck(2750 K)) est de compenser le fort déficit de couleur bleu dont souffrent les lampes flat-field généralement utilisées.

Le terme entre [ ] dans l'équation (8) est l'expression de la "réponse instrumentale" dans le référentiel ISIS, ou pseudo réponse (on appelle aussi parfois ce terme "la solution en flux" de l'instrument). La courbe de Planck synthétique permet d'obtenir une réponse approximativement plate en fonction de la longueur d'onde, ce qui l'on constate effectivement. Une anomalie dans la réponse est ainsi plus facile à repérer.

Avec la formule 10, on remarque qu'effectivement, le contenu spectral P de la lampe flat-field détermine l'aspect de la pseudo réponse instrumentale. Ce profil par exemple évoluer à l'allumage de la lampe, alors que le filament n'a pas encore atteint la température d'équilibre. L'expérience montre cependant que les effets de couleurs sont toujours modestes, même avec une lampe halogène branchée sur le secteur 220V.

Noter sur cette page : https://buil.astrosurf.com/dispersion/atmo.htm, comment la dispersion atmosphérique et la turbulence atmosphérique peuvent affecter le profil spectral. Les risques d'erreur augmentent au fur et à mesure que la fente devient étroite en regard de la dimension du disque de seeing. Je travaille dans un site extrêmement turbulent. Le seeing est le plus souvent supérieur à 3 secondes d'arc et atteint environ 4 à 5 secondes d'arc une nuit sur deux. J'ai utilisé ici une configuration instrumentale qui réduit les conséquences photométriques de ce très mauvais seeing. La distance focale du télescope n'est que de 840 mm. Un seing de 5 secondes d'arc représente environ 21 microns au foyer. La fente du spectrographe Alpy 600 étant large de 23 microns, une large part du flux entre donc malgré tout dans le spectrographe, ce qui limite les problèmes photométriques liés à l'agitation et au spectre atmosphérique.

Observation de l'objet PNV J19150199+0719471 avec le système de guidage Alpy 600. Il s'agit d'une nova naine en éruption,
de magnitude V = 12,06 au moment de l'observation (source AAVSO). La fente d'entrée est le trait sombre
vertical (bien visible à cause de la pollution lumineuse). Elle fait 23 microns de large, soit environ 5,6 arcsec sur le ciel
compte tenu de la focale du télescope (D = 212 mm, F/4). De gauche à gauche à droite, l'étoile cible est progressivement
amenée au centre de la fente. A ce moment précis, elle disparaît presque totalement.
Le FWHM (seeing) est mesuré égal à 4 arcsec. L'étoile est donc un peu plus fine que la largeur de la fente. C'est une configuration proche
de l'idéal pour capturer l'essentiel du flux stellaire et pour réduire les conséquences de la dispersion atmosphérique sur
le continuum. Le télescope lui-même est parfaitement achromatique. Caméra de guidage est un modèle Atik314L+.
Le temps de pose est de 15 secondes lors de cette phase de pointage.

La configuration de guidage. Le temps de pose n'est plus ici que de 2 secondes.
L'étoile cible de magnitude 12 est virtuellement invisible lorsquelle est dans la fente.
Le guidage est réalisé sur une étoile brillante du champ, il n'y a pas d'autre choix, et
cela fonctionne très bien. La logiciel de guidage est Audela. La monture équatoriale est une
un modèle Astrophysics GTO Mach 1.

Pour intégrer les mouvements erratiques de l'image de l'étoile sur la fente d'entrée du spectrographe, il est recommandé d'acquérir le spectre des étoiles de référence avec un temps d'intégration de 30 secondes au minimum. Ne jamais donc utiliser une étoile aussi brillante que Vega comme référence avec des spectrographes aussi lumineux qu'un LISA ou un Alpy 600 – le temps de pose est bien trop court (environ 1 sec.) car il faut éviter de saturer le détecteur.

 Retour