Stage de spectrographie - Session 2 (2/4)

LA CONSTRUCTION D'UN SPECTROGRAPHE

Raymond - De quoi est fait au juste un spectrographe ?

Aude - Le coeur de l'instrument est un composant optique qui disperse la lumière incidente dans les couleurs de l'arc-en-ciel. On peut pour cela utiliser un prisme en verre. Tenez le prisme à bout de bras et observez un paysage au travers :

Les objets apparaissent subitement irisés des couleurs de l'arc-en-ciel. Vous venez de construire un spectrographe très primitif ! Mais la simplicité du prisme cache aussi pas mal de défauts. Un prisme disperse relativement modestement la lumière et de façon différente suivant la longueur d'onde. Ces considérations posent pas mal de problèmes lors de la réalisation d'un vrai spectrographe et lorsqu'il s'agit d'analyser les spectres. Bien qu'il soit tout à fait possible de concevoir un spectrographe avec un prisme, je vais m'orienter vers un autre dispositif que l'on appelle réseau à diffraction.

Christian - Diantre !

Aude - Un réseau à diffraction est une pièce optique sur laquelle on grave des sillons rectilignes très rapprochés, typiquement avec une densité de plusieurs centaines de traits au millimètre. Supposons que la gravure soit réalisée sur une surface réfléchissante. Lorsque la lumière blanche arrive sur une telle structure, au lieu de repartir avec un angle de réflexion égal à l'angle d'incidence, comme pour un miroir, elle subit un phénomène de diffraction auquel s'ajoute un phénomène d'interférence. La conséquence est l'apparition d'un spectre tel que le montre la figure suivante :

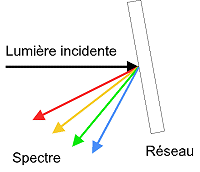
Vous pouvez facilement voir comment fonctionne un réseau en examinant la lumière d'une lampe qui se réfléchie sur un Compact Disk . Un disque optique comporte une sorte de sillon très mince qui s'enroule sur toute sa surface et qui se comporte optiquement comme les traits d'un réseau. En orientant de manière adéquate le disque vous aller immanquablement observer un spectre.

Faisons un petit peu de mathématique pour mieux voir comment fonctionne un réseau.

Christian - Ouille !

Aude - N'ai pas peur Christian, il y a pratiquement qu'une seule formule à connaître. C'est la formule dite des réseaux. Supposons que la lumière incidente soit monochromatique, c'est à dire constituée d'une seule longueur d'onde...

Raymond - C'est le type de lumière que l'on trouve à la sortie des lasers, non ?

Aude - Tout à fait. Soit l la longueur d'onde de cette lumière. Elle arrive sur le réseau avec l'angle d'incidence q1. L'angle d'incidence est l'angle que fait le faisceau en arrivant sur le réseau avec la normale au plan du réseau, le tout compté dans le plan d'incidence.

Christian - (soupir) La normale, le plan d'incidence ?

Aude - La normale c'est une droite qui est perpendiculaire à la surface du réseau. Le plan d'incidence c'est un plan qui passe par le rayon incident et le rayon diffracté. Dans ma figure, le plan d'incidence c'est la surface de la feuille.

Christian - (rassuré) Je vois !

Aude - L'orientation des traits du réseau est quant à elle perpendiculaire au plan de la feuille, c'est important. Après diffraction, la lumière repart en faisant l'angle q2 par rapport à la normale, tel que :

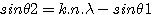
avec n le nombre de traits gravés par millimètre, l la longueur d'onde de la lumière en millimètre et k un coefficient qui peut prendre toutes les valeurs entières ...-3, -2, -1, 0, 1, 2, ... On appelle k l'ordre du spectre. Les différentes valeurs de k sont valides à tout moment, ce qui signifie que le faisceau diffracté est en fait un ensemble de rayons correspondant notamment aux diverses valeurs de k. La figure suivante montre la définition des angles :

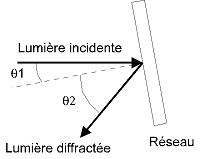
La figure que je viens de dessiner montre un réseau dit à réflexion : les traits sont gravés sur une surface réfléchissante, constituée d'une fine couche d'aluminium par exemple. Il existe une autre disposition où les traits sont gravés sur un support transparent. Le comportement du réseau est similaire à ceci près que la lumière le traverse, comme le montre cette figure :

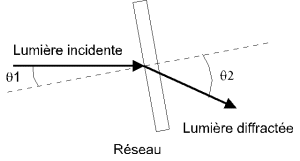
Prenons des exemples numériques. Soit un réseau gravé avec une densité de 600 traits par millimètre. La longueur d'onde de la lumière incidente est de 5700 angstroms, soit 0,57.10^-3 millimètre. Enfin, nous supposons que l'angle d'incidence est de 10°. Voici le résultat pour quelques valeurs de k :

k=-2 :

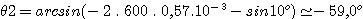
k=-1 :

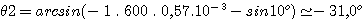
k= 0 :

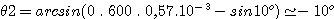
k=+1 :

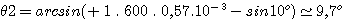
k=+2 :

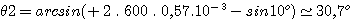
k=+3 :

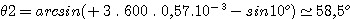
etc.

Lorsque les angles d'incidences et de diffraction sont de mêmes signes, cela signifie que les rayons sont du même coté de la normale au réseau.

Si maintenant vous modifiez la valeur de la longueur d'onde, vous allez obtenir une autre valeur de l'angle de diffraction. C'est pour cela qu'un spectre coloré qui s'étale angulairement à la sortie du réseau lorsque la lumière incidente est blanche.

L'angle entre le faisceau incident et le faisceau diffracté pour une certaine longueur d'onde est donné par :

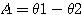
Le résultat pour k=0 est particulier car, d'une part, quel que soit la longueur d'onde incidente, le faisceau diffracté a toujours le même angle, d'autre part, l'angle d'incidence et l'angle de diffraction sont identiques mais de signes opposés. Pour k=0, le réseau se comporte donc comme un simple miroir.

Raymond - J'ai du mal à comprendre. Tu as calculé plusieurs valeurs de l'angle du faisceau après son passage sur le réseau. Est-ce que cela signifie que la lumière monochromatique qui arrive se divise en autant de rayons ?

Aude - Oui, si tu projète sur un écran la lumière en retour du réseau tu va voir effectivement plusieurs images. Regardez l'expérience suivante. J'ai éclairé un réseau à transmission avec un laser qui émet dans une lumière constituée d'une seule longueur d'onde : un très beau rayon rouge. Après avoir traversé le réseau on observe une grande quantité d'images arrivant sur l'écran. L'une de ces images correspond à la traversée directe, pour k=0, les autres correspondent aux déviations calculées pour les valeurs k=-2, k=-1, k=1, k=2, etc.

Maintenant, si vous imaginez un laser émettant un lumière de longueur d'onde un peu différente, la position des points d'impacts sur le réseau va elle aussi être légèrement différente. Si à présent vous prolongez le raisonnement pour une lumière non plus monochromatique, mais polychromatique, qui contient simultanément un large spectre de longueur d'onde continu, vous allez observer sur l'écran autant spectres colorés qu'il y a d'ordres.

Raymond - Mais qu'est ce que je vais faire avec tous ces spectres ? Il n'y en a qu'un seul qui m'intéresse a priori ?

Aude - Exact, il va falloir choisir un ordre et considérer les autres comme des parasites. Ils sont du reste parasite sur deux plans. Tout d'abord on peut montrer avec la formule du réseau que pour certains ordres et certaines longueurs d'onde les spectres se recouvrent d'un ordre à l'autre. Par exemple, à la position dans le spectre associée à la longueur d'onde de 8000 angstroms pour l'ordre +1 vous trouvez aussi une lumière correspondante à la longueur d'onde de 4000 angstroms provenant de l'ordre +2. Ensuite, la luminosité des spectres est atténuée puisque la quantité de lumière incidente se distribue dans les différents ordres. Pour régler ce dernier problème les fabricants de réseau gravent les traits avec un profil particulier qui permet de concentrer un maximum de lumière dans un ordre donné, et même dans une certaine région spectrale de cet ordre. On appelle cela le "blaze" du réseau. Par exemple si dans le catalogue d'un constructeur vous trouvez l'expression "blazé à 5000 angstroms pour l'ordre 1" cela signifie que le réseau concentre un maximum d'énergie dans l'ordre 1 autour de la longueur d'onde de 5000 angstroms, et cela au détriment des autres ordres.

Christian - Tous les réseaux ont cette propriété ?

Aude - Non malheureusement. Parfois les réseaux très économiques ne sont pas blazé, ce qui rend leur usage très problématique en astronomie à cause de la faible luminosité. Un réseau correctement blazé concentrera par exemple 80% de la lumière dans un ordre donné, alors que la version non blazé se contentera d'envoyer quelques pourcents dans les différents ordres, l'essentiel de la lumière passant par l'ordre zéro, ce qui n'est pas très utile.

Raymond - Je reviens à ma question, quel spectre dois- je choisir ?

Aude - La différence entre un spectre d'ordre 1 et un spectre d'ordre 2 est que le second est deux fois plus étalé que le premier. Sur le papier, le spectre d'ordre 2 est le plus intéressent puisqu'il offre une meilleure résolution spectrale. Mais en astronomie il faut aussi jouer avec la luminosité très faible des astres, et la résolution spectrale n'est pas obligatoirement le paramètre prépondérant d'un spectrographe, je vous l'ai déjà signalé. On voit aussi qu'à l'ordre 2, les angles de réfraction sur le réseau sont plus important qu'à l'ordre 1, ce qui oblige dans le premier cas à utiliser des réseaux de grandes tailles et donc coûteux. Enfin, la région spectrale bénéficiant du blaze est plus étroite dans l'ordre 2 que dans l'ordre 1. Par exemple un réseau blazé pour l'ordre 1 à la longueur d'onde de 5000  angstroms sera utilisable avec une efficacité correcte pour tout l'ensemble du spectre visible. En revanche, le même réseau utilisé dans l'ordre 2 ne sera efficace que dans une région spectrale deux fois plus étroite. Toutes ces raisons font qu'il est généralement préférable de travailler à l'ordre 1 plutôt qu'à des ordres élevés. Si on souhaite agir sur la valeur de la dispersion angulaire, au lieu de jouer avec les ordres de diffraction, il est préférable de sélectionner un réseau ayant le nombre adéquat de traits par millimètre. On trouve dans le commerce des réseaux gravés avec des densités allant de 100 à 2400 traits/mm.

Alain - Je suppose que dans un spectrographe il n'y a pas qu'un réseau ?

Aude - Ce serait trop facile ! Regardez le schéma suivant :

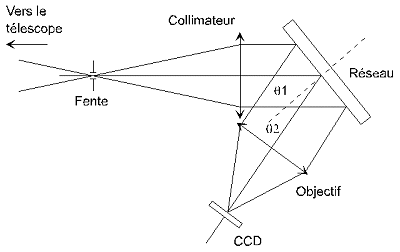
En suivant le sens de la lumière, vous trouvez tout d'abord une fente qui isole une petite région du ciel au foyer du télescope. Cette fente est suivie d'une première lentille qui envoie l'image de la fente à l'infini. Pour ce faire, le foyer de la lentille, que l'on appelle dans le cas présent une collimatrice, coïncide avec la position de la fente. C'est un faisceau de lumière parallèle qui arrive donc sur le réseau.

Raymond - Cette lentille est-elle vraiment indispensable ? Ne serait-il pas possible de mettre le réseau juste derrière la fente, cela simplifierait pas mal le spectrographe il me semble ?

Aude - Pour des raisons optiques, un peu difficiles à expliquer ici, il faut admettre que les systèmes dispersifs n'aiment pas du tout recevoir un faisceau de lumière arrivant sous la forme d'un cône. Cela introduit des aberrations optiques qui détruisent la qualité du spectre. S'il faut absolument placer un réseau dans un faisceau convergeant par exemple, cela doit être effectué dans des conditions très particulières. Par exemple, le réseau doit être très proche du foyer de l'instrument et comporter peu de traits au millimètre. Mais dans sa forme la plus traditionnelle, retenez qu'un spectrographe comporte toujours un collimateur, qui est l'ensemble constitué de la lentille collimatrice et de la fente.

Raymond - Qu'elle est la fonction de la fente au juste ?

Aude - Hum, c'est une question compliquée, je réserve la réponse pour tout à l'heure !

Après le passage dans le collimateur un faisceau de lumière parallèle arrive donc sur le réseau. Celui-ci diffracte la lumière et on se retrouve donc avec plusieurs spectres correspondant aux différents ordres. Notez bien que dans la figure précédente, les traits du réseau sont gravés perpendiculairement au papier. Une seconde lentille, dite objectif de caméra, est placée en regard du réseau, en face d'un des ordres. Le spectre correspondant se forme alors sur la surface sensible du capteur CCD, qui est au foyer de l'objectif.

Je vous le rappelle, on choisit de préférence le spectre du premier ordre. Pour cela il faut respecter des angles précis entre le faisceau arrivant du collimateur, la normale au réseau et la direction de l'axe optique de l'objectif. J'ai remis la définition des angles q1 et q2 dans le schéma du spectrographe.  A votre avis, si le réseau à 600 traits/mm et si l'angle d'incidence du faisceau est de 10°, quel doit être l'angle entre l'axe du collimateur et l'axe de l'objectif ?

Christian - (fièrement) J'ai la réponse ! C'est A=q1-q2. Puisque l'angle d'incidence est de 10°, on a q1=10°. D'après les calculs de tout à l'heure, si j'utilise l'ordre 1, j'ai q2=9,7°. Donc la réponse est 10°-9,7°=0,3°.

Aude - Bien vu mon petit Christian, mais il y a un problème. Regarde le schéma du spectrographe. Est-ce que tu as l'impression que l'angle entre l'axe du collimateur et l'axe de l'objectif est de 0,3°, c'est à dire une valeur pratiquement nulle ?

Christian - (déçu) Pas vraiment, il doit être de l'ordre de 45°. Il ne marche pas ton spectrographe !!!

Aude - Il marche parfaitement si au lieu de prendre l'ordre +1 tu prends l'ordre -1. Dans ce cas tu as bien q1=10°, mais cette fois q2=-31°. L'angle recherché est alors 10°-(-31°)=41°. C'est bien plus conforme à ce que montre la figure.

Christian - Tu es forte Aude (oeil pétillant) !

Raymond - Les ordres -1 et +1 sont-ils vraiment équivalent ?

Aude - Oui et non. Oui car la dispersion angulaire du spectre est semblable pour ces deux ordres. Non car le choix de l'ordre -1 permet d'ouvrir suffisamment l'angle entre le collimateur et l'objectif pour pouvoir disposer physiquement les lentilles. Ce ne serait pas possible ici en travaillant à l'ordre +1. Bien sur, vous devez ajuster les valeurs de q1 et q2 en fonction du nombre de traits par millimètre du réseau et de la dimension physique de vos lentilles.

Je vous montre en vrai comment se présente un spectrographe. Ce n'est tout de même pas très compliqué. Je pense que vous allez facilement reconnaître les éléments, à ceci près que la fente est ici absente :

Dans cet exemple le réseau à 1200 traits par millimètre et j'ai choisit les valeurs d'angles q1=35°et q2=4,3° pour la longueur d'onde de 5700 angstroms à l'ordre +1. L'écart angulaire entre l'axe de l'objectif et l'axe du collimateur est donc égal ici à A=35°-4,3°=30,7°. De cette manière les rayons lumineux de la longueur d'onde 5700 angstroms arriverons au centre du capteur CCD. Vous pouvez bien sur sélectionner une autre longueur d'onde centrale, par exemple 6563 angstroms, si vous souhaitez étudier la raie rouge de l'hydrogène. Pour cela vous avez le soit le choix de modifier légèrement la valeur de l'angle A lors de la construction du spectrographe, soit le choix de faire pivoter le réseau. Cette dernière solution permet de modifier la longueur d'onde centrale en cours d'observation, ce qui est bien pratique. L'axe de rotation doit passer par le plan gravé du réseau.

Toujours à propos des angles, vous vérifierez que le spectrographe précédent fonctionne de manière semblable si vous faites q1=4,3° et q2=35°. Cependant pour une raison que je ne vais pas développer ici, il est toujours préférable de choisir la combinaison d'angles pour laquelle q2 est plus petit que q1. Ceci améliore la qualité des spectres.

Christian - Admettons... (dubitatif)

Aude - Si je t'assure, c'est un problème d'anamorphose.

Christian - D'ana... OK je te crois !

Aude - Vraiment je t'assure. Dans les calculs que nous avons fait au début nous avions le couple q1=10° et q2=-31° pour l'ordre -1. Je recommande de permuter les valeurs des angles en faisant q1=-31° et q2=10°.

Raymond - Je vois que tu utilise des objectifs photographiques en guise de lentilles...

Aude - C'est une bonne solution car la qualité image n'est généralement pas mauvaise, en tout cas très supérieure à celle fournie par de simples lentilles minces. L'avantage d'un objectif photographique est qu'il est relativement bien corrigé du chromatisme, du moins dans la partie visible du spectre. De plus, il offre un champ large pour des rapports d'ouverture assez élevés. C'est ce qu'il nous faut !

Raymond - J'ai tout un stock d'objectifs photographiques dans mon grenier. Je peux utiliser n'importe lequel ?

Aude - Non, il y a des règles de construction. Il est particulièrement important de maîtriser la valeur de la dispersion linéaire en angstroms par pixel dans l'image CCD. Voici la formule à connaître. Si P est cette dispersion en angstroms par pixel, nous avons :

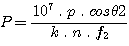
avec p la taille des pixels du CCD en millimètre et f2 la distance focale de l'objectif.

Supposons par exemple que l'on utilise un réseau à 600 traits par millimètre (n=600) au premier ordre (k=1) et que la caméra est équipée d'un CCD Kodak KAF-0400 de 768x512 pixels de 9 microns de coté (p=9.10^-3 mm). L'angle q2 pour la longueur d'onde de 5700 angstroms est de 10°. Enfin, nous choisissons d'utiliser un objectif photographique standard de 50 mm de focale (f2=50). L'application numérique donne :

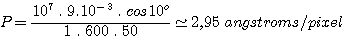
Si on oriente le CCD de manière à ce que le spectre s'étale le long de la plus grande dimension de la surface sensible, l'étendue spectrale visible dans une image sera de 768 x 2,95 = 2266 angstroms. Si la longueur d'onde au centre du spectre acquis est de 5700 angstroms, alors les longueurs d'onde extrêmes observables sont :

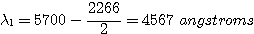
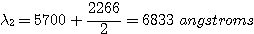
Cet intervalle spectral couvre une bonne partie du spectre visible. Les raies importantes de l'hydrogène à 6563 Å et 4761 Å sont ainsi observables directement.

Raymond - Et si au lieu d'utiliser un objectif de 50 mm j'adopte un objectif de 100 mm de focale, d'après t'es formule, la taille du spectre augmente, n'est-ce pas ?

Aude - En utilisant un objectif de focale deux fois plus longue la dispersion linéaire double bien sur, mais le domaine spectral exploré dans une même image CCD diminue aussi d'un facteur deux. C'est une question de compromis. Nous allons nous en tenir dans notre petit spectrographe à un objectif de 50 mm de focale.

Raymond - Et pour la collimatrice...

Aude - Le choix est nettement plus libre. Une règle d'or absolue cependant. La distance focale de la collimatrice doit être au moins égale ou supérieure à celle de l'objectif. Dans notre exemple, la distance focale de l'objectif collimateur est obligatoirement égale ou supérieure à 50 mm. Si vous violez cette règle vos spectres ne seront pas de bonne qualité : ils vont perdre de la résolution.

Je vais ici choisir un objectif photographique de 135 mm de distance focale. Un grand standard dans les focales photographiques, et je suis sure Raymond que tu as cela dans un carton.

Raymond - Exact, tu as deviné. J'ai un bon vieil objectif de 135 mm ouvert à 2,8.

Aude - Tu as raison de parler de rapport d'ouverture. Il faut que je vous dise quelque chose d'important à ce propos. Je redessine le schéma du spectrographe en faisant apparaître le diamètre des faisceaux optiques :
 

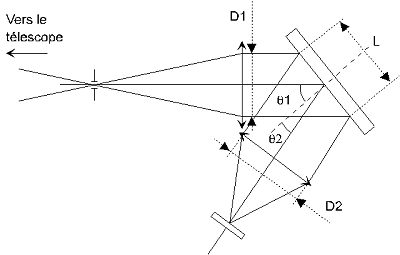
J'ai fait figurer le diamètre du faisceau D1 à la sortie du collimateur, la largeur L du faisceau dans le plan d'incidence sur le réseau, et le diamètre D2 du faisceau à l'entrée de l'objectif.

La formule qui donne le diamètre D1 est :

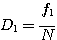
avec f1 la distance focale du collimateur et N le rapport d'ouverture du télescope. On va supposer que le télescope est un Schmidt-Cassegrain équipé d'un réducteur de focale qui donne un rapport d'ouverture de F/D=6,3. Pour un objectif collimateur de 135 mm de focale on trouve alors :

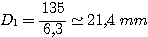
A ce stade il faut vérifier que certaines parties du faisceau optique provenant du télescope ne sont pas interceptées par des éléments mécaniques de l'objectif collimateur, causant alors un vignettage optique. Ce n'est pas le cas ici puisque ton objectif, Raymond, est plus ouvert que le télescope (f/2,8 pour f/6,3), il y a même une bonne marge. Si j'assimile le téléobjectif à une lentille simple, son diamètre est égal à 135/2,8=48mm. C'est largement suffisant pour transmettre un faisceau optique de 21,4 mm de diamètre.

La quantité L nous informe sur la dimension minimale à donner au réseau à diffraction pour qu'il n'y ai pas de vignettage. Elle est calculée par la formule :

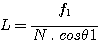
avec q1=31° on trouve :

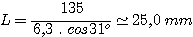
Un réseau de 30x30 mm de surface gravée serait ici un bon choix, avec une marge satisfaisante.

Il nous reste à calculer le diamètre D2 minimum que doit avoir l'objectif. Voici la formule qui permet de le calculer :

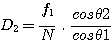
Faisons l'application numérique :

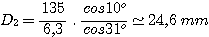
Si on suppose que l'objectif photographique de 50 mm est ouvert à f/1,8, il peut être assimilé à une lentille unique et mince de diamètre 50/1,8=27,8 mm. Ce diamètre est suffisant pour collecter le faisceau collimaté de 24,6 mm provenant du réseau, mais il s'en faut de peu, la marge n'étant que de 1,6 mm sur le rayon.

Alain - La vie est belle !

Aude - Attention ! Le diamètre du faisceau que nous venons de calculer n'est valable que pour une longueur d'onde, à savoir 5700 angstroms. Vous savez qu'après diffraction sur les traits du réseau un spectre se forme. Ce sont tous les rayons provenant de ce spectre qu'il faut si possible récupérer avec l'objectif, tout au moins ceux qui correspondant à l'intervalle spectral délimité par la dimension du CCD. Sur la figure suivante, le diamètre utile de l'objectif doit être suffisant pour collecter à la fois les rayons rouges et bleus pour ne pas vignetter certaines parties du spectre.

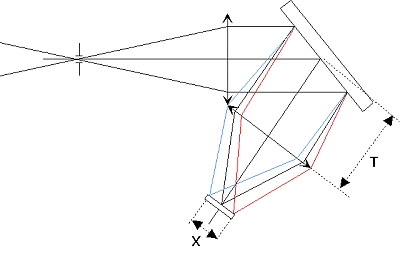
Le problème est d'autant plus critique que la lentille frontale de l'objectif est éloignée de la surface du réseau.

La formule complète pour calculer une valeur approximative de la dimension D2 en tenant compte de la dispersion angulaire est :

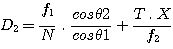
avec T la distance entre la lentille frontale de l'objectif et la surface du réseau et avec X la dimension linéaire du CCD suivant l'axe de la dispersion. Cette dernière quantité vaut 6,9 mm avec un CCD KAF-0400.

On note qu'il y a vraiment tout intérêt à diminuer la valeur T, c'est à dire approcher l'objectif du réseau. Pour déterminer jusqu'où il est possible d'aller je vous recommande de faire une épure optique en vous servant de votre logiciel de dessin favori ou même en découpant des petits papiers à l'échelle. Vous devez bien prendre en compte le contour mécanique de vos composants optiques. Voici un exemple qui correspond aux paramètres instrumentaux de notre exemple. J'ai utilisé les vrais dimensions d'un objectif de 135 mm et d'un objectif de 50 mm (de marque Nikon). Ne pas oublier non plus le contour de la caméra CCD, ici une Audine :

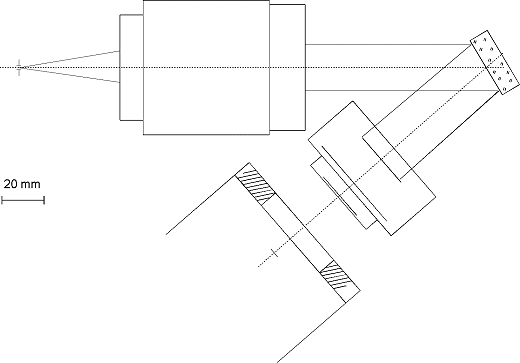
On peut relever sur cette épure que la valeur de T ne peut être bien inférieure à 67 mm. Faisons dans ces conditions le calcul numérique de D2 :

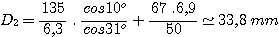
La pupille d'entrée de l'objectif photographique ne faisant que 50/1,8 = 27,8 mm, il s'avère qu'en dehors d'une région au centre du spectre, celui-ci est progressivement vigneté en allant vers le bord du champ.

Alain - Mais il suffit d'utiliser un objectif photographique plus ouvert. Si je ne me trompe pas, avec un objectif de 50 mm à f/1,2, le diamètre de faisceau accepté est de presque 42 mm. Cela nous sauve.

Raymond - Comme tu y va Alain, un tel objectif peux être bien coûteux. Attention au budget spectro !

Aude - Alain à raison, la manière la plus directe pour résoudre le problème est de se procurer un objectif très ouvert. Mais effectivement, il risque de revenir assez cher à l'achat. Pour donner une idée, au prix du neuf, un objectif Nikon de 50 mm à f/1,8 coûte de l'ordre de 250 Euros, alors de la version à f/1,4 tourne vers 480 Euros. Outre l'avantage de solutionner dans certains cas le problème du vignettage optique, le second objectif devrait en principe donner des images de meilleures qualité, c'est à dire des raies un peu plus fines.

Alain - Ca ce manifeste de quelle manière ?

Aude - Un empâtement des raies spectrales ou une forme asymétrique de ces mêmes raies. Voici la coupe dans le spectre d'émission du gaz neon observé en bord de l'image CCD. A gauche en utilisant un objectif Nikon de 50 mm f1.8 et à droite en utilisant le modèle Nikon f1.4 :

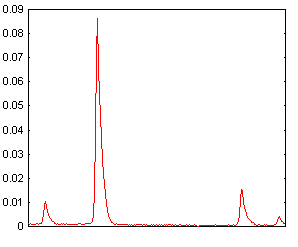
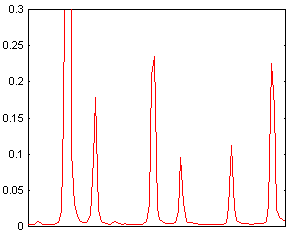
C'est assez subtile, mais l'image de droite est un peu meilleure. La résolution spectrale est très légèrement supérieure et surtout, la forme bien symétrique des raies permet un meilleur étalonnage spectral. Nous verrons cette opération plus tard.

Alain - Soit, mais que faire si on ne peux investir un somme aussi importante ?

Aude - Pas d'inquiétude. Les différences restent tout de même modestes entre les optiques sur le plan de qualité, et en la matière c'est un petit peu au bonheur la chance : il n'est pas rare qu'une optique chère possède des défauts sévères à cause d'un contrôle qualité un peu sommaire chez le fabriquant. Dans la mesure du possible, choisissez des objectifs de grandes marques pour réduire un peu ce type de désagrément. Pour ce qui concerne les problèmes de vignettage, vous pouvez vivre avec. Dans notre exemple avec un objectif de caméra ouvert a F1,8 le défaut de vignettage fera perdre de l'ordre de 20% du flux aux extrémités du spectre. Pas entièrement satisfaisant, mais pas non plus absolument dramatique. La correction en flux des spectres, que nous verrons lors des sessions suivantes, permettra de corriger sans trop de problème l'effet photométrique induit par le vignettage.

Une autre solution consiste à adopter un objectif collimateur de focale un peu plus courte. Ici un objectif de 90 à 100 mm conviendrait parfaitement.

Augmenter le rapport d'ouverture du télescope est encore une solution. Dans le cas présent un télescope ouvert à F/D=8 permettrait d'éliminer le vignettage optique. Mais, il n'est pas vraiment toujours possible de jouer avec ce paramètre.

Enfin, nous l'avons vu, il reste la possibilité d'utiliser un objectif plus ouvert (f/1,4). D'une manière générale il faut retenir que c'est l'objectif qui suit le réseau qui pose le plus de problème dans un spectrographe, car il doit être généralement très ouvert.

Christian - Et la fente ?

Aude - D'accord j'y viens. Supposez que l'on place à l'entrée du spectrographe un trou de diamètre s et que celui-ci soit éclairé par une source de lumière monochromatique. Le spectre sur le CCD se résume l'image du trou à un endroit précis suivant l'axe de la dispersion correspondant à la longueur d'onde monochromatique. Eclairez à présent le trou avec une lumière présentant un spectre continu, avec en plus de fines raies sombres en absorption. Comme précédemment, les raies dans le spectre qui se forme sur le CCD sont alors autant d'images monochromatiques du trou. La largeur de ces raies est étroitement liée au diamètre du trou, ou plus précisément au diamètre s' de l'image du trou d'entrée sur le CCD. Plus petite dimension est cette dimension, meilleur est le pouvoir séparateur du spectrographe. La valeur de s' est donnée par :

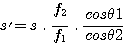
soit avec les paramètres de notre spectrographe :

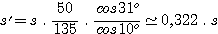
Soit un diamètre du trou d'entrée de 50 microns, son image sur le CCD a un diamètre de 0,322 . 50 = 16 microns. Dans ce cas, la largeur des raies spectrales est approximativement égale à deux pixels du CCD, ce qui est correct au niveau de l'échantillonnage du spectre.

Raymond - L'échantillonnage ?

Aude - Un théorème connu dit que pour pouvoir distinguer un détail d'une image il faut que ce détail soit couvert par au moins deux pixels. S'il y a moins de deux pixels, on dit que le détail est sous-échantillonné, et il ne pourra pas être résolu. Si en revanche les pixels sont petits par rapport à la taille du détail que l'on souhaite voir, on dit que ce dernier est sur-échantillonné. Un sur-échantillonnage ne fait jamais de mal en général lorsqu'il est modéré, disons d'un facteur 3 ou 4. La situation des deux pixels par éléments d'images que l'on veut résoudre est le cas limite d'échantillonnage, et suffisant pour séparer le détail en question. C'est plus clair Raymond ?

Raymond - Ca va, ca va.

Christian - Si je comprends bien, tout à l'heure on a calculé que la dispersion spectrale est de 2,95 angstroms par pixels et puisque la largeur des raies à cause du diamètre du trou est de 2 pixels, j'en déduit que la résolution spectrale est de 2. 2,95 = 5,9 angstroms. J'ai juste ?

Aude - ...

Christian - Ben, Aude !

Aude - ...

Alain - Coucou Aude !!!

Aude - Excusez-moi, je méditais au travail que l'on fait ensemble. Je trouve que l'on avance bien et ça me fait plaisir.

Raymond, Alain, Christian - Nous aussi Aude !

Aude - Bien..., Christian tu as pratiquement juste, la résolution spectrale devrait être proche de 6 angstroms. Cependant, il faut prendre en considération les aberrations optiques des composants du spectrographe, qui ont tendance à la dégrader. On parle de résolution instrumentale lorsqu'il est question de l'affectation de la qualité image par les composants du spectrographe eux-même, en dehors du trou ou de la fente d'entrée. On peut s'attendre ici à une résolution spectrale de 7 à 8 angstroms au final, ce qui correspond bien au but cherché initial.

J'en profite pour introduire un terme que vous aller souvent rencontrer en spectrométrie : le pouvoir de résolution, que l'on désigne généralement par la lettre R. Supposons qu'au voisinage de la longueur d'onde de 5700 angstroms la largeur des raies soient de 8 angstroms. Plus précisément cette la largeur doit être mesurée à mi-hauteur de l'amplitude de la raie. On appelle cela aussi le FWHM, de l'anglais Full Width Half Maximum. Alors le pouvoir de résolution est R=5700/8=712, valeur que l'on arrondie à 700. En gros, pour R inférieur à 1 000 on parle de basse résolution spectrale, entre 1 000 et 10 000 on parle de moyenne résolution, et au-dessus, de haute résolution. Les grands spectrographes professionnels peuvent avoir des pouvoirs de résolution de plus de 100 000.

Raymond - Je suppose qu'au fur et à mesure que la résolution augmente, le spectrographe devient gros ?

Aude - Tout à fait. Du reste si le spectrographe est vraiment très encombrant il ne peut plus être monté sur le télescope et on est amené à utiliser une fibre optique pour véhiculer le faisceau optique depuis le foyer du télescope jusqu'au spectrographe, situé par exemple dans une pièce bien climatisée. La sortie de fibre prend alors la place du trou d'entrée du spectrographe et c'est le diamètre de la fibre que l'on assimile au diamètre de ce trou. Les fibres de plus petit diamètre que l'on peut raisonnablement utiliser font 100 microns de diamètre. Avec notre petit spectrographe l'image de la fibre couvre à présent 32 microns, si bien que la résolution spectrale commence à être dégradée significativement. Dans une telle situation, le seul levier sur lequel on puisse agir est le rapport f2/f1 comme le montre la dernière formule. Il faut que la distance focale de la lentille collimatrice soit longue par rapport à la lentille objectif. Mais le corollaire est que les optiques seront de grand diamètre et donc chère. Le spectrographe va aussi prendre de l'envergure.

Retour à la page d'accueil du stage                  Page précédente                   Page suivante