SPECTROPHOTOMETRIE
Exemples pratiques avec le logiciel ISIS

Christian Buil

http://www.astrosurf.com/aras/

Click here for an English version of the page

SOMMAIRE

PARTIE 1 : COMMENT EXPRIMER LES SPECTRES EN UNITE ENERGETIQUE
    - Méthode 1 : à partir de 4 spectres
    - Méthode 2 : à partir de 2 spectres

PARTIE 2 : COMMENT EVALUER LES MAGNITUDES A PARTIR DE SPECTRES EN FLUX

PARTIE 3 : COMMENT EFFECTUER LE RATTACHEMENT A UN SYSTEME PHOTOMETRIQUE

PARTIE 4 : LA MESURE "INSTANTANEE" DE LA TRANSMISSION ATMOSPHERIQUE

PARTIE 5 : COMMENT PREDIRE LE SIGNAL PRODUIT PAR UNE ETOILE DONNEE

Dans la partie 1 de ce document, on propose deux méthodes pour convertir l’intensité en valeurs exprimées en unité physique. Les méthodes exposées sont des techniques spectrophotométriques précises qui peuvent fortement valoriser les spectres acquis pour certains travaux.

La méthode 1 nécessite de réaliser 4 spectres : un spectre en fente étroite de la cible à étalonner, un spectre en fente étroite d'une étoile de référence voisine dans le ciel, un spectre en fente large de la cible, un spectre en fente large de la référence.

La méthode 2 nécessite de réaliser seulement deux spectres : un spectre de l'étoile cible et un spectre de l'étoile de référence.

La seconde méthode est clairement la plus simple et c'est sûrement la technique "officielle" dans la plupart des observatoires. Elle est cependant moins précise que la méthode 1 car la transmission relative de la fente entre la mesure de l'étoile cible et de l'étoile de référence (liée au seeing, à la qualité de suivi du télescope, à l'angle parallactique) peut ne pas être la même. Je suggère même dans le texte, pour limiter les erreurs, d'exploiter la méthode 2 avec une fente large pour des applications qui demandent une grande précision photométrique.

Noter que seule la méthode 2 est applicable à un spectrographe échelle équipé d'une fibre optique.

D'autres méthodes sont possibles. Voir en particulier cette procédure (F. Teyssier) qui mélange à la fois la photométrie traditionnelle (imagerie avec un filtre passe-bande) et la spectrographie, mais elle est moins directe que les techniques présentées ici, qui ne font fait appel qu'à des données spectrale et un seul instrument.

La partie 2 montre comment exploiter les spectres exprimés en unité énergétique pour en extraire les magnitude BVR.

La partie 3 montre sur un exemple pratique comment établir les équations de rattachement à un système photométrique et ainsi produire de mesures en magnitude précisent.

La partie 4 indique comment exploiter les sensibilités instrumentales pour évaluer rapidement la transmission de l'atmosphère terrestre et améliorer encore la qualité des mesures photométriques.

Enfin, la partie 5 est une exploitation de tout ce qui est dit précédemment pour calculer le bilan radiométrique d'une chaîne complète d'observation.
 

ETAPE 1

Je commence la méthode la plus complexe... (tout est relatif, il n'y a rien de vraiment compliqué dans tout ce qui va suivre, il suffit de pratiquer pour s'en appercevoir !)

Charger en mémoire le spectre d'une étoile dite de référence. Ici le spectre de l'étoile HD196544 de magnitude V=5,428, extrait de la base MILES (cette base est intégrée dans l'application ISIS). L'intensité dans ce spectre est exprimée en intensité relative (normalisée à l'unité à 6700 A environ).

Sauvegarder le profil dans un fichier FITS. Par exemple, le nommer : REF_HD196544.FIT.

ETAPE 2

Ce profil de référence s'exprime en intensité relative (arbitraire donc). Notre but est de le convertir en un profil s'exprimant en unité physique. Ici nous choisissions des ergs/cm²/s/A (flux énergétique).

Ceci est possible car on connaît la magnitude V de l'étoile (c'est une donnée catalogue).  Ouvrir l'onglet "Outils", puis l'onglet "Traitement spectres 3" et faire comme indiquer dans la copie d'écran à droite.

ISIS utilise la formule suivante pour réaliser la conversion en flux :

ETAPE 3

Les intensités dans le fichier REF_HD196544_FLUX.FIT sont donc maintenant en unité physique. Afficher ce spectre dans ISIS.

Note : ISIS 5.3.0 et au dessus intégre une partie des standards de la base CALSPEC ( http://www.stsci.edu/hst/observatory/cdbs/calspec.html ) dans laquelle les spectres s'expriment directement en ergs/cm2/s/A. Il s'agit cependant d'objets relativement faibles. Si vous travaillez sur des cibles brillantes, il faut créer vous-même votre pseudo standard spectrophotométrique en déroulant les étapes 1 et 2.

ETAPE 4

Choisir une longueur d'onde de référence. Le choix est en général quelconque (4750, 5500 A,...), mais ici on sélectionne une longueur d'onde correspondant à une zone assez plate dans le continuum du spectre science (ce sera le spectre de la nova Delphini 2013 observés le 29.8 août 2013).

La longueur d'onde de référence choisie est lo = 6100 A. A cette longueur d'onde, dans le profil MILES exprimé en unité physique on relève une intensité de

Fo = 1.81 x 10^-11 erg/cm²/s/A

(c'est un flux hors atmosphère).

ETAPE 5

Traiter le spectre de l'objet science de manière tout à fait standard. Ce spectre est observé avec une fente étroite (ici de 23 microns de large). Le résultat s'exprime en intensité relative. Par la suite, ce spectre est désigné par la lettre 'a'. L'équipement pour réaliser ce spectre est un spectrographe Aply 600 monté sur un télescope Celestron 11. La caméra science est un modele Atik460EX.

A droite, le spectre réduit en intensités relatives de la nova Delphini 2013 (la zone de normalisation à la valeur unitaire est comprise ici 6650 A et 6680 A, mais vous pouvez faire un tout autre choix).

L'intensité relative trouvée à la longueur d'onde de référence (6100 A) est dans cet exemple :

Fa = 0.827

Note : Le profil ci-contre a été calculé en tenant compte de l'atténuation spectrale instrumentale et atmosphérique. Le plus simple pour évaluer ces paramètres est d'observer une étoile angulairement proche de la cible, ce qui atténue les problèmes de réfraction atmosphérique et réduit l'absorption différentielle. Dans l'exemple le spectre 'a' de la nova Delphini 2013 est traité en se servant d'un spectre de l'étoile HD196544 de type A2V observé dans les mêmes conditions (fente de 23 microns) et situé non loin angulairement.
 

ETAPE 6

La fente d'entrée produit une atténuation du flux stellaire. Cette atténuation n'est pas constante dans le temps. Elle est liée à la turbulence, aux erreurs de guidage, au chromatisme de l'atmosphère, ...

Pour enregistrer tout le flux stellaire indépendamment de l'effet fente, il est nécessaire d'élargir cette dernière. Dans l'exemple à droite, je réalise un spectre avec un spectrographe Alpy 600 en positionnant momentanément l'étoile dans la partie large d'une fente spéciale, dite "photométrique". Un accessoire commode et puissant ici.

Avec un spectrographe Lhires III ou LISA par exemple, vous pouvez tout simplement retirer la fente. L'autoguidage ne fonctionne à cet instant, mais ce n'est pas très critique si les objets sont brillants (poses courtes - pas d'autoguidage). Les spectres sont par ailleurs un peu défocalisés, mais ce n'est pas non plus très gênant : le flux est dilué spatialement et spectralement, mais il est correctement mesuré. Mieux, sur ces mêmes spectrographes, il est possible d'interchanger facilement les fentes : si vous en avez la possibilité montée une fente large dans la phase d'acquisition du spectre photométrique, faite le.

On réalise de la même manière un spectre de la cible scientifique et un spectre de l'étoile de référence (ou standard).
 

ETAPE 7

Traiter les spectres "photométriques" (obtenus avec une fente large) le plus simplement possible.

D'abord, entrer des valeurs nulles pour la zone de normalisation. Il est très important aussi de ne pas sélectionner l'option de sommation pondérée des spectres (choisir "Addition simple").

Choisir une zone de binning bien large pour être sûr d'intégrer tout le flux stellaire lors du calcul du profil spectral.

Pour le traitement, vous n'avez même pas besoin de définir une image FLAT et un fichier de réponse instrumentale. Aller au plus simple.

ETAPE 8

Voici le résulat pour le spectre "photométrique" de l'étoile de référence.

L'intensité s'exprime ici en comptes numériques car nous avons mis à zéro la valeur des bornes de la zone de calcul du continuum.

Nous désignons ce spectre par la lettre 'b'.

Le signal mesuré à la longueur d'onde de référence est :

Fb = 27020 ADU

Le temps de pose est noté Tb. Ici il est de Tb = 180 secondes.

ETAPE 9

Faite un traitement strictement identique pour le spectre de l'objet cible, en se servant d'une fente photométrique (ou en retirant la fente ou en permutant une fente large). A droite pour le spectre de la nova. On désigne ce spectre par la lettre 'c'.

A la longueur d'onde de référence, on mesure un signal

Fc = 7682 ADU

Le temps de pose est noté Tc. Ici il est Tc = 150 secondes.

ETAPE 10

On calcule le coefficient C, qui est le facteur de conversion entre les intensités relatives dans le spectre 'a' et le flux hors atmosphère :

C = ( Fo Fc Tb ) / (Fa Fb Tc)

Faisons l'application numérique dans l'exemple :

C = ( 1.81 x 10-11  x  7682 x 180 ) / ( 0.827  x  27020  x 150 )
=  7.47 x 10^-12

On multiple le spectre 'a' (réalisé avec une fente étroite) par cette valeur (voir la copie d'écran à droite).

Attention : on fait ici l'hypothèse que la cible scientifique à étalonner et l'étoile de référence sont observées à une masse d'air voisine et sur un intervalle de temps assez court (en fonction de la qualité photométrique de la nuit).

ETAPE 11

Voici le résultat, le spectre de la nova Delphini 2013 étalonné en flux absolu (ergs/cm²/s/A), comme si l'objet était vu en dehors de l'atmosphère terrestre. Ce spectre ainsi étalonné devient propre à des analyses astrophysiques avancées.

ETAPE 1

Ci-contre, le profil spectral observé de l'étoile de référence sélectionné (ici HD196544).

Ce profil est étalonné en longueur d'onde, mais il n'est pas corrigé de la réponse instrumentale. Il s'exprime en pas codeur pour le temps d'intégration, qui est ici de 6 x 30 s = 180 secondes.

Rappelez-vous (voir la méthode 1), pour obliger ISIS à ne pas normaliser les spectres, entrer des valeurs nulles dans les champs longueur d'onde de la zone de normalisation depuis l'onglet de "Réglages".

Pour annuler les effets de fente, ce spectre a été ici obtenu avec la fente photométrique du spectrographe Alpy 600 (largeur de 230 microns).

Notez bien cependant que la fente soit étroite ou large, la méthode 2 s'applique strictement de la même manière.

Le risque d'une fente étroite est d'abaisser significativement la précision de mesure en flux.

Un conseil : mesurez le signal dans une succession de 10 à 20 spectres brut d'un même objet et analysez la dispersion des valeurs. En général, les mauvaises nouvelles arrivent à ce stade. L'écart type de la distribution observée donne une idée de l'erreur de mesure. Testez de cette manière la qualité de votre procédure.

ETAPE 2

A droite, le même profil que précédemment, mais ramené en nombre de pas codeur mesurés par pixel et pas seconde.

Pour cela, l'intensité du spectre mesuré à l'étape 1 est simplement divisé par le temps de pose (180 secondes).

Ce spectre est appelé 'a' dans la suite.

ETAPE 3

Le spectre de notre pseudo standard (HD196544) exprimé en unité de flux (voir la méthode 1), extrait de la base MILES.

La résolution de ce spectre a été dégradée par convolution avec une fonction gaussienne pour être amené à la même résolution que le spectre Alpy 600 (ici en utilisant l'outil "Filtre" de ISIS avec un coefficient de 7).

Ce spectre est appelé 'b' dans la suite.

ETAPE 4

Le rapport spectre 'a' / spectre 'b'.

Le résultat est la courbe de sensibilité de la chaine instrumentale. Elle inclue l'ensemble instrumental (réseau, détecteur, ...) mais aussi l'extinction atmosphérique pour la masse d'air d'observation.

Plus précisément, cette courbe représente le signal observé par échantillon spectral (ici l'échantillon spectral représente 2,5 A environ), en une seconde seconde de temps de pose, intégré sur l'ensemble de la surface collectrice du télescope et pour l'extinction atmophérique correspond à l'élévation de l'astre, alors que le flux incident est de 1 erg/cm²/s/A.

Noter que les pertes de signal associées aux effets de fente n'interviennent pas ici car la dite fente est très large par rapport au disque de seeing.

ETAPE 5

Le profil spectral observé de la nova Delphini 2013.

Le profil effectif a été ici divisisé par le temps de pose, qui est ici de 150 secondes. Les intensités s'expriment donc en ADU /seconde/pixel.

ETAPE 6

Le résultat final : le spectre de la nova mesuré en unité de flux.

On l'obtient simplement, en divisant le spectre observé (en ADU/pixel), rammené à un temps de pose de 1 seconde, par la courbe de sensibilité.

Dans le graphe ci-contre on compare les spectres trouvés en suivant la méthode 1 et la méthode 2. Le résultat est très proche !

Bien sur la méthode 2 est la plus simple (moins d'acquisitions à réaliser) et c'est sûrement celle-ci qui est la plus utilisée dans les observatoires. Elle demande cependant quelques précautions et présente des limites.

Les détails méritent d'être examinés...

En examinant la partie rouge du spectre, on constate que la méthode 2 a permis d'éliminer les raies telluriques. C'est normal, car la courbe de sensibilité calculée à l'étape 4 de la méthode 2 inclut l'effet de la transmission atmosphérique. Lorsqu'on effectue ensuite l'étape 6, le profil est donc automatiquement ramené à ce qu'il serait en observant depuis l'espace.

Une raie d'émission à 7250 A apparaît alors clairement dans le spectre issu de la méthode 2, alors qu’elle est noyée dans une bande d'absorption de la vapeur d'eau dans le spectre calculé selon la méthode 1.

Examinons à présent la partie du bleu du spectre.

La méthode 1 donne clairement un profil spectral où les raies spectrale sont plus intenses (et fines). La raison est simple : dans la méthode 2 le spectre est exclusivement mesuré en se servant d'une fente large, du coup, la résolution spectrale est dégradée, et d'où l'effet constaté.

Dans la méthode 2, les détails du profil sont donc fonction du seeing et des erreurs de guidage. Il faut donc être prudent lorsqu'on interprète la forme et l'intensité au pic des raies. En revanche, la largeur équivalente est inchangée entre les deux profils.

Une solution consiste à mettre en œuvre la méthode 2 en ne se servant que d'une fente étroite. Mais attention, dans cette situation les distorsions photométriques induites peuvent être fortes si on observe loin du zénith et a un fort angle parallactique. Voir en particulier cette page :

https://buil.astrosurf.com/alpy600/photometric_slit.htm

et les effets dans des situations extrêmes (et provoquées !) :

https://buil.astrosurf.com/dispersion/atmo.htm

Le problème de fente est réduit si l'étoile de référence et la cible sont voisines angulairement (ce qui doit être la règle). Il subsiste malgré tout une erreur photométrique liée à l'erreur de positionnement de l'étoile sur une fente étroite. L'intérêt de la fente large est d'annuler quasiment totalement cet effet - la qualité spectrophotométrique peut alors être meilleure que le dixième de magnitude.
 

Dans la partie ultra-violette, le spectre obtenu avec la méthode 2 présente un bruit plus élevé.

Cela vient de l'incertitude qui porte sur le calcul de la courbe de sensibilité (étape 4). Si les spectres 'a' et 'b' ne présentent pas un profil très voisin dans ces détails, on produit des artefacts (pseudo bruit) qui n'ont rien à voir avec la courbe de réponse effective.

Pour pallier à ce dernier problème, assez sérieux, car dans certaines circonstances il peut induire des distorsions dans les raies qui peuvent êtres mal interprétées, je recommande vivement de calculer une courbe de réponse soigneusement lissée (par exemple en utilisant l'outil "Continuum" de ISIS). Lors du calcul, je demande au logiciel d'éliminer les raies telluriques et les raies de l'hydrogène majeures. Dans ces circonstances, l'usage d'une image flat-field est recommandé (spectre d'une lampe blanche tunsgtène).

Cette version de la courbe de sensibilité instrumentale (réponse) ne gomme pas les raies telluriques dans le profil final (malheureusement). En revanche, la remontée de bruit est minimisée. C'est une question de choix.

Le spectre de la nova Delphini 2013 réduit à partir de la méthode 2 et un courbe de sensibilité lissée.

ETAPE 1

Charger et afficher le spectre à analyser exprimé en unité photométrique physiques (en erg/cm²/s/A). La manière de calculer les intensités en unité physique est expliquée dans la partie 1 de cette page.

Le spectre à droite est celui d'un standard photométrique. Il est issu de la très connue séquence photométrique d'étoiles Landolt. Les astronomes professionnels utilisent fort souvent ces objets pour réduire les données photométriques. Il s'agit d'un vaste ensemble d'étoiles, pour la plupart localisées dans les zones Selected Area (SA), de tout type spectral, dont ont connaît la magnitude BVRI précise dans le système photométrique Johnson-Cousins. Ce sont de très bons standards photométriques secondaires. Ici nous avons le spectre de l'étoile SA 112-275.

Voir ici une liste et cartes de champs des objets Landolt : http://james.as.arizona.edu/~psmith/tableA.html

Le spectre à droite est réalisé avec un spectrographe Alpy 600 monté sur un télescope Celestron 11 (D = 0.28 m). Le temps de pose est de 5 x 240 secondes.

Pour calculer les intensités en unités énergétiques dans ce spectre j'ai calculé la sensibilité globale du système d'observation (elle inclue la réponse de l'instrument et la transmission de l'atmopshère) à partir d'un spectre réalisé de l'étoile HD204041 (le profil est extrait de la base MILES). J'ai choisi cet objet car il se trouve à la même masse d'air que SA 112-275.

Pour convertir les intensités en comptes numériques dans le spectre de l'étoile SA 112-275 en erg/cm²/s/A j'ai utilisé la méthode 2 décrite dans la partie 1.

ETAPE 2

Téléchargez le profil spectral des bandes synthétiques du système BRV Bessel (voir plus bas). Celles-ci couvrent la partie photovisuelle du spectre.

Dans le bleu, la longueur d'onde valide la plus courte est 3750 A. On estime qu’en deçà de cette limite, les spectres présentent trop de bruits pour êtres utilisables correctement.

Dans le rouge, la longueur d'onde limite est 7400 A afin d'éviter les problèmes de recouvrement d'ordre, caractéristiques des spectrographes à réseau - voir ci-contre. Autrement dit, la bande R est tronquée dans sa partie rouge. Nous verrons les conséquences plus loin.

Les fichiers filtre :

BESSEL_B.FIT
BESSEL_V.FIT
BESSEL_R.FIT

ETAPE 3

Multiplier le profil de l'étoile analsée, exprimé en flux énergétique, par le profil d'un filtre, par exemple ci-contre, le filtre Bessel B.

Pour cela, ouvrir l'outil "Arithmétique", et calculer le produit des deux spectres. Le résultat apparait à l'écran (la copie d'écran correspond à la version 5.3.1 de ISIS).

ETAPE 4

Le résultat  est le flux de l'étoile pondérée par la courbe de transmission du filtre numérique.

ETAPE 5

On mesure le flux énergétique traversant le filtre numérique en intégrant le signal observé. Pour cela, ouvrir l'outil "FWHM", puis faire un double click tout à gauche du profil, puis un double click tout à droite. Comme le montre la copie d'écran ci-contre.
 

ETAPE 6

L'information importante retournée est le flux énergétique intégré, tel qu'il se présente dans la copie d'écran à droite. Elle est calculée en tenant compte de l'échantillonnage du spectre analysé.

Ici, la valeur intégrale dans la bande B calculée est :

Fb = 2,184 x 10^-10 erg/cm²/s

ETAPE 7

Vous pouvez procéder de la même manière avec les filtres V et B (recharger au prélable de spectre analysé bien sur).

Voici le résultat trouvé pour les bandes V et R :

Fv = 4,048 x 10^-10 erg/cm²/s

Fr = 1,751 x 10^-10 erg/cm²/s

ETAPE 8

Il reste à calculer les magnitudes B, V et R associées au flux trouvé.

On évalue d'abord les magnitudes instrumentales avec la formule de Pogson :

Bo = -2,5 log ( Fb )
Vo = -2,5 log ( Fv )
Ro = -2,5 log ( Fr )

Dans l'exemple on trouve :

Bo = 24,152
Vo = 23,636
Ro = 23,068

Le passage entre les magnitudes instrumentales (Bo, Vo, Ro) et les magnitudes exprimées dans le système Johnson-Cousins ce fait au travers du système d'équations suivant (attention, les paramètres sont propresb à l'instrumentation utilisée, ici un télescope C11 et un spectrographe Alpy 600 couplé à une caméra CCD modèle Atik460EX) :

B = Bo - 13,028 - 0,01 x (Bo - Vo)
V = Vo - 13,730
R = Ro - 13,753 - 0,10 x (Vo - Ro)

Tout calcul fait, on trouve par la mesure :

B = 11,119
V = 9,906
R = 9,258

Pour mémoire les magnitudes données par Landolt sont B = 11,115, V = 9,905 et R = 9,258. L'accord est voisin du 1/100 de magnitude, ce qui constitue une fort bonne photométrie.

La question qui se pose : comment sont évalués les termes de l'équation de passage entre les magnitudes instrumentales et les magnitudes vraies (rattachées à un système photométrique) ? Ces paramètres sont associés à un instrument particulier et ils doivent donc être évalués par vous au moins une fois (comme ils sont très stables, vous aurez rarement à y revenir, si ce n'est pour affiner votre modèle).

La réponse à cette question importante fait l'objet de la partie 3 de cette page.

Classiquement le lien entre les magnitudes instrumentales Bo, Vo, Ro et les magnitudes photométriques B, V, R se fait au travers d'un système simple d'équations linéaires :

B = Bo - Zb - ab x (Bo - Vo)
V = Vo - Zv - av x (Bo - Vo)
R = Ro - Zr - ar x (Vo - Ro)

Avec Zb, Zv et Zr les points zéro de l'échelle des magnitudes, respectivement des bandes B, V et R.

Les paramètres ab, av et ar sont des termes de couleurs, qui servent à corriger l'effet de l'écart entre la bande passante des filtres spectraux effectifs (et de la chaine instrumentale) et la bande passante utilisée par Landolt lors de l'établissement de son catalogue photométrique. On estime que le système de filtre exploité est cohérent avec le système photométrique lorsque les coefficients ab,  av et ar ont des valeurs inférieures à 0,5. Cette condition permet de limiter les erreurs lorsqu'on mesure des spectres particuliers (Mira, nova, ...).

Pour évaluer les termes de l'équation de passage, j'ai observé 3 étoiles des séquences Landolt (situées dans la zone équatoriale) avec la configuration C11 + Alpy 600. Voici les données catalogues de ces étoiles :

La courbe de réponse du système, ou de sensibilté, est calculée à partir de l'observation de l'étoile HD204041, située à la même masse d'air que les étoiles Landolt :

Voici le spectre des 3 étoiles Landolt observées. Les spectres sont convertis en unité de flux grâce à la courbe de sensibilité précédemment établie :

Dans ces trois spectres, le flux intégré est calculé dans les bandes BVR Bessel, suivant la méthode présentée dans la première partie de cette page, ainsi que la magnitude instrumentale. Les tableaux suivants montrent le résultat des mesures. On rappelle dans les tables la magnitude Landolt attendue. Enfin, on donne le zéro de l'échelle des magnitudes par bande en utilisant les formules simplifiées de passage suivantes (je ne tiens pas compte du terme de couleur dans un premier temps) :

B = Bo - Zb
V = Vo - Zv
R = Ro = Zr

Malgré la non-prise en compte du terme de couleur, le zéro des magnitudes (par bande) est remarquablement constant pour les étoiles observées. Cela signifie que la procédure employée est juste, que la mesure des flux avec un petit spectrographe comme Alpy 600 est extrêmement précise et que le système de filtre synthétique employé est très cohérent avec le système BVR Johnson-Cousin. La dispersion du zéro est de l'ordre de 1/100 de magnitude dans les bandes B et V. Elle est légèrement moins bonne dans la bande R à cause de la troncature du filtre à 7400 A.

A la main, on trouve facilement un terme de couleur qui améliore encore le paysage (le coefficient de couleur ne vaut que 0,1 en bande R et 0,01 en bande B, c'est-à-dire quasiment rien dans cette dernière bande)  Voici au final les équations de rattachement adopté (en exploitant seulement trois étoiles Landolt) :

B = Bo - 13,028 - 0,01 x (Bo - Vo)
V = Vo - 13,730
R = Ro - 13,753 - 0,10 x (Vo - Ro)

Voici les erreurs résiduelles trouvées avec ce système d'équations :

La précision observée est significativement meilleure que 0,01 magnitude (avec la prudence requise, du fait que l'on a observé ici que trois étoiles de référence).

Cette analyse fait le lien entre spectrographie et photométrie. Elle montre qu'il est enviseable pour certaines applications de substituer efficacement les mesures spectrophotométriques à des mesures photométriques traditionnelles. On peut noter aussi une différence de taille : en photométrie classique on ne produit que 3 éléments d'information dans le domaine photovisuel, alors qu'avec un spectromètre, on extrait simultanément plusieurs centaines d'éléments d'informations du signal.

Pour clore cette partie, un petit complément concernant le contrôle de la validité des équations de passage. La base de données du logiciel ISIS contient en effet tous les éléments qui permettent de vérifier les calculs précédents. En s'appuyant sur des spectres d'étoiles déjà étalonnées en flux et en appliquant les filtres numériques BRV, on peut s'assurer de la valeur des magnitudes calculées en les comparants à celles de la littérature. Prenons un exemple.

Dans ISIS, depuis l'onglet "Profil", ouvrir l'outil "Database". Dans la sous-base CALSPEC, choisir l'étoile BD+25 4655, puis cliquer sur le bouton "Afficher" :

L'étoile BD+25 4655 est un standard spectrophotométrique assez brillant, très souvent utilisé dans les observatoires terrestres et spatiaux pour étalonner en flux les spectres acquis avec les instruments. Il s'agit d'une étoile très chaude (Teff = 43000 K), pauvre en hydrogène et riche en hélium. Les raies de l'hélium neutre et ionisé une fois dominent le spectre. Les raies de l'hydrogène sont discrètes et le continuum est relativement plat :

A partir de l'outil "Arithmétique", multipliez ce spectre par le profil du filtre Bessel B :

Calculez ensuite le flux intégré dans la bande du filtre avec l'outil "FWHM". On trouve ici Fb = 1,076 x 10^-9 erg/cm²/s. Traduit en magnitude instrumentale avec l'aide de la formule de Pogson, ce flux correspond à Bo = +22,420.

Le même calcul en utilisant le filtre Bessel R donne pour l'étoile BD+25  4655, Fv = 4,401 x 10-10 et Vo = +23,391.

L'indice Bo-Vo vaut ici Bo-Vo = -0,971. En introduisant ces valeurs dans les formules de passages établies ci-devant, on trouve pour cette étoile :

B = 9,40
V = 9,66

Les valeurs SIMBAD pour cet objet sont :

B = 9,39
V = 9,68

L'écart n'est que de quelques centièmes de magnitude. Nos formules de passages sont donc correctes.

Toujours à titre de vérification (et d'exercice), vous pouvez aussi observer physiquement l'étoile de référence et ainsi contrôler de manière globale l'exactitude de votre travail.

Ci-après on trouve un spectre observé de BD+25 4655 avec un Celestron 11 et un spectrographe Alpy 600. Le rapport signal est très élevé, ce qui constitue le premier garant d'une bonne mesure :

PARTIE 4 :
LA MESURE "INSTANTANEE" DE LA TRANSMISSION ATMOPHERIQUE

On décrit ici le déroulement des opérations permettant de prédire le signal mesuré en nombre de comptes numériques en un point choisi du spectre pour d'une étoile donnée.

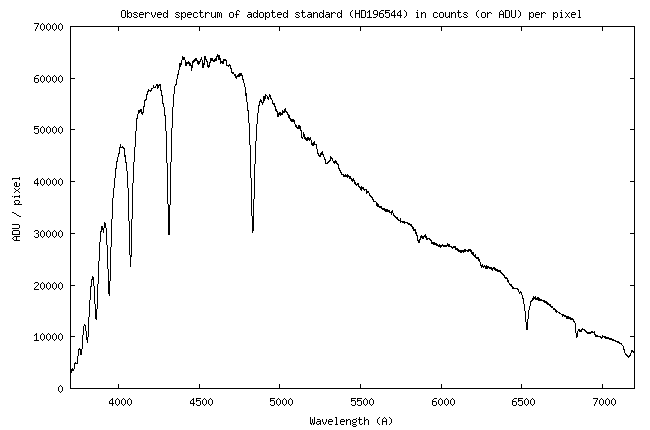
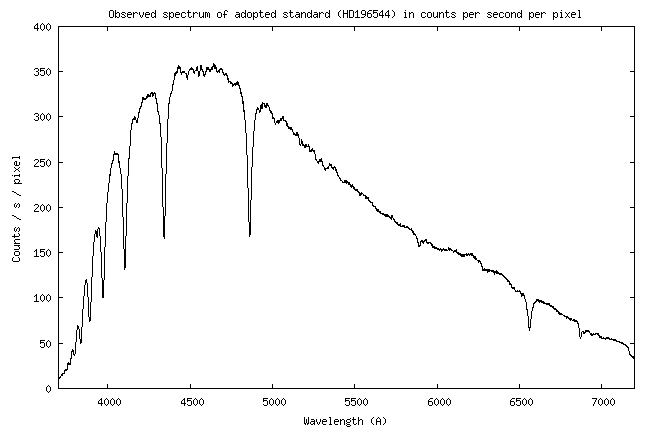
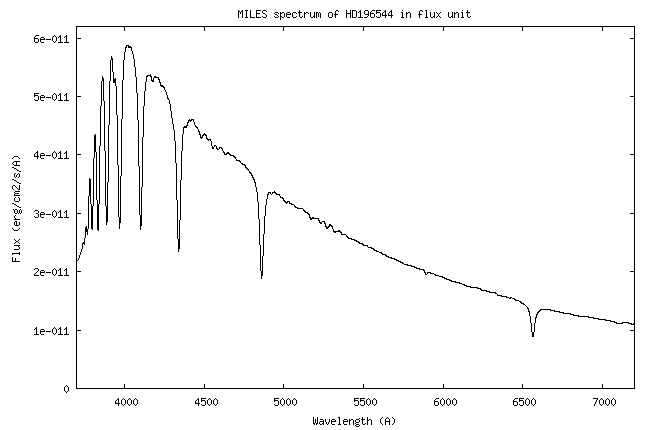
Pour cette démonstration je vais me servir de la courbe de sensibilité du système instrument établit lors de l'observation de l'étoile HD196544, alors que celle-ci était à une élévation de 57,08° au-dessus de l'horizon, soit une masse d'air de 1,191. Lors de la nuit d'observation en question, l'atmosphère était bien pure. Le AOD (Aerosol Optical Depth) a été mesuré à 0,09 à partir de l’observation de deux étoiles à des élévations différentes (voir la partie 4).

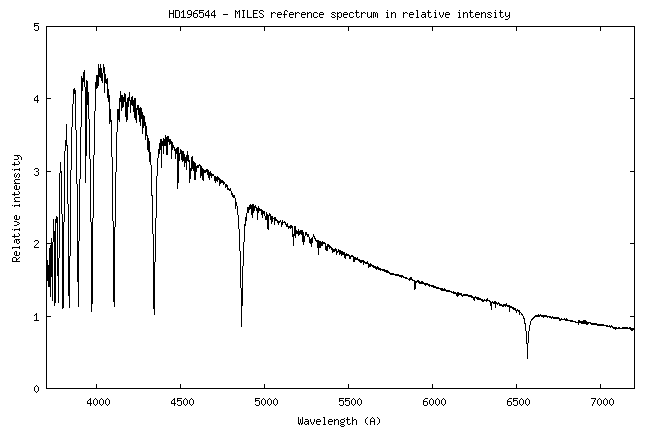
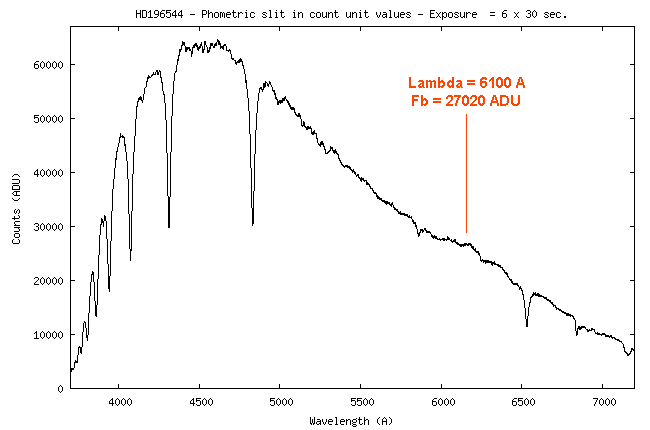
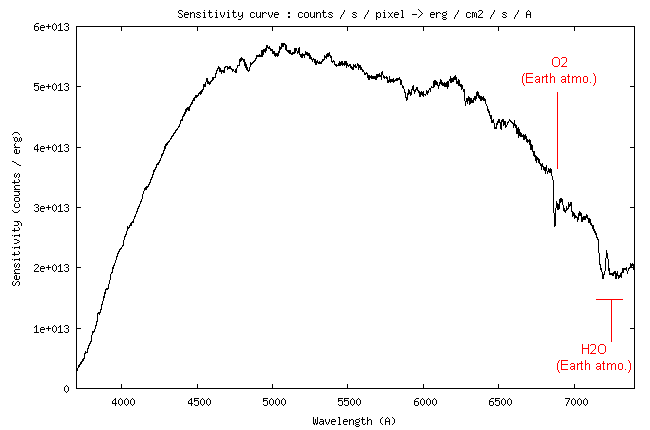
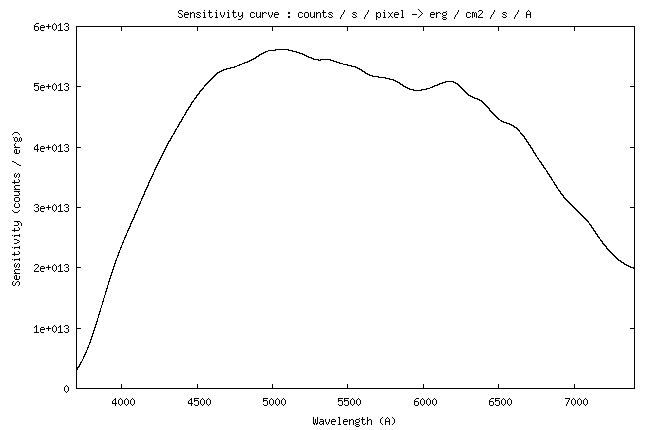
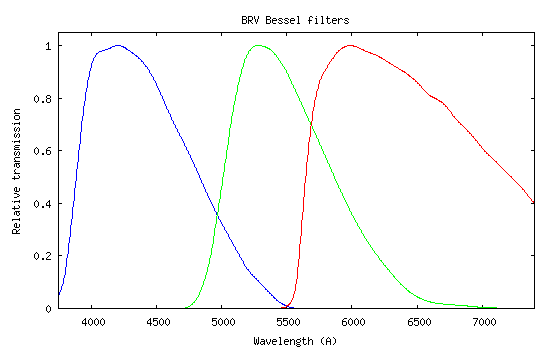
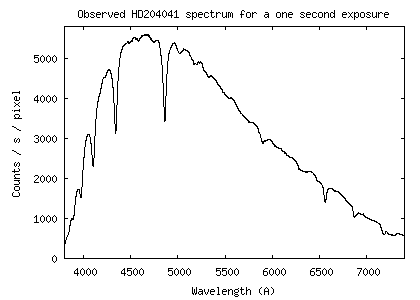
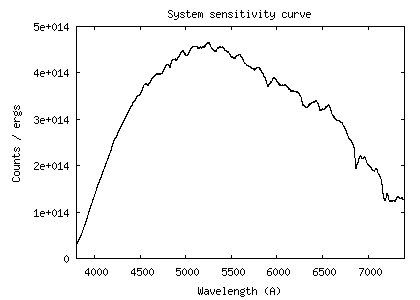
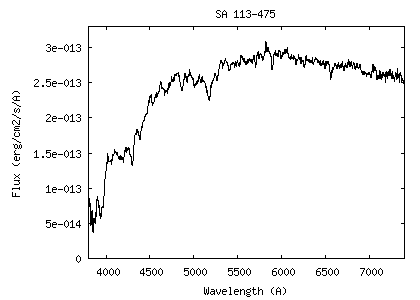
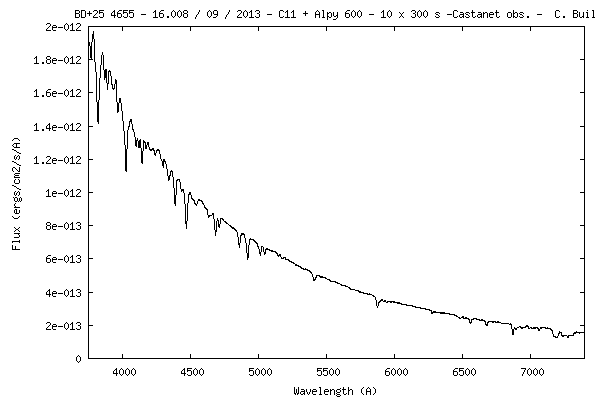
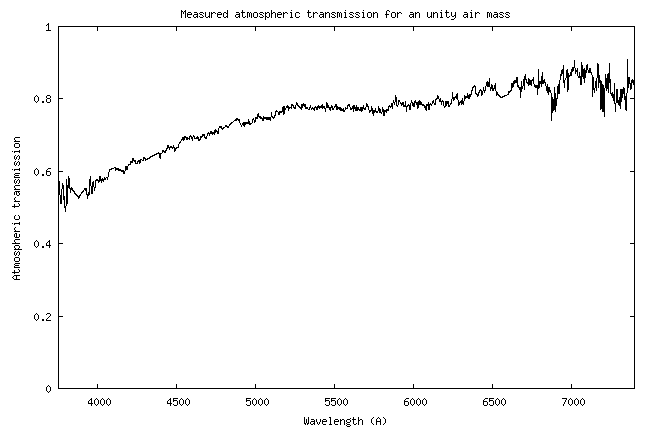
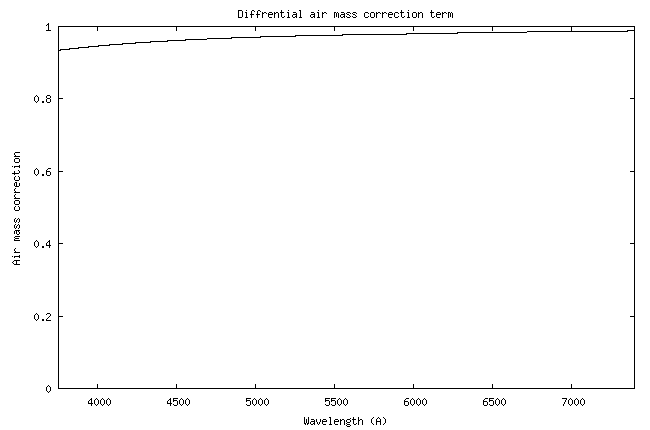
Voici la courbe de sensibilité relevée :

Je rappelle que cette courbe fait le lien entre les comptes numériques (signal en ADU = Analog Digital Unit) observés dans un échantillon du spectre (après bien sur le retrait du signal d'offset, du dark et du fond de ciel) et un flux incident de 1 erg/cm²/s/A pour la longueur d'onde considérée reçu par l'entrée du télescope (voir la partie 1, méthode 2). La sensibilité est ramenée à un temps de pose de 1 seconde.

Le télescope est un Celestron 11, le spectrographe un Alpy 600 et la caméra un modèle Atik460EX exploitée en binning 2x2.

Je choisis arbitrairement d'effectuer le calcul à la longueur d'onde de 5550 A. Vous pouvez bien sur sélectionner un tout autre point du spectre.

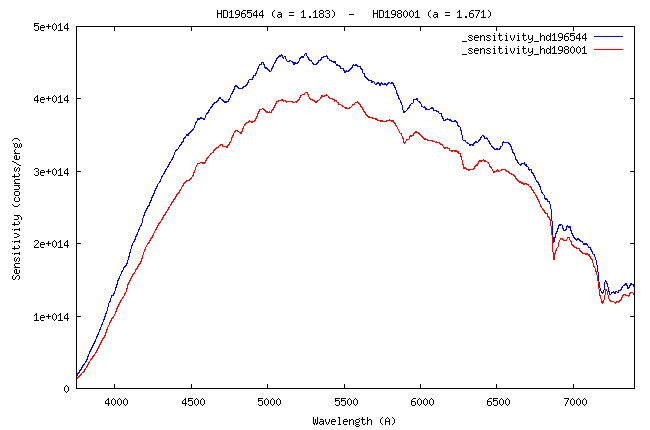
A la longueur d'onde de 5550 A, la valeur de la sensibilité instrumentale est de 4,26 x 10¹⁴ (ADU)/(erg) - voir la courbe.

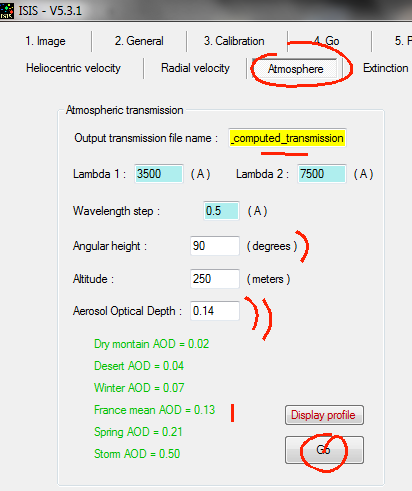
On va calculer le nombre de ADU qui serait comptabilisé si l'instrument était situé en dehors de l'atmosphère terrestre. On calcule la transmission atmosphérique avec l'outil "Atmosphère" de l'onglet "Divers" pour H = 57,08° et AOD = 0,09 :

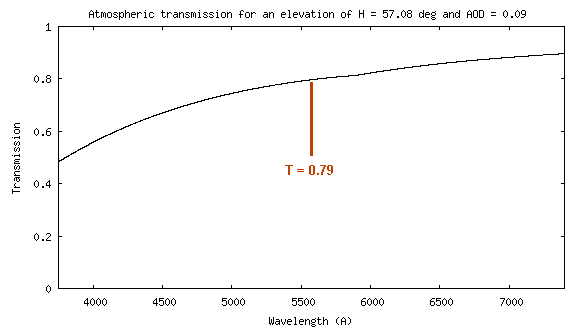
Le signal observé hors atmosphère serait donc : So = 4,26 x 10¹⁴ / 0,79 = 5,39 x 10¹⁴ (ADU)/(erg).

C'est cette valeur que l'on va chercher à retrouver par le calcul.

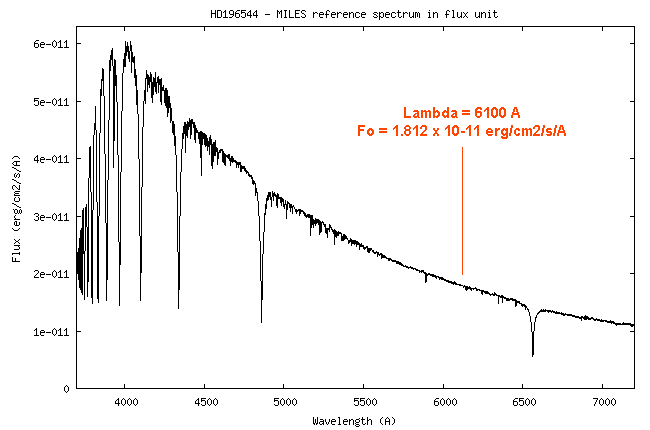
Soit donc une étoile produisant un flux hors atmosphère de Fo = 1 erg/cm²/s/A.

Par commodité on convertit ce flux énergétique en un flux No compté en nombre de photons/cm²/s/A.

La formule de conversion entre le flux exprimé en ergs et le flux exprimé en photons est

No = (Fo x l ) / (1,9861 x 10^-8)

avec l, la longueur d'onde exprimée en Angstroms.

Faisons le calcul :

No = (1 x 5550) / (1,9861 x 10-8) = 2,79 x 10¹¹ photons/cm²/s/A

C'est précisément le nombre de photons reçus de notre étoile dans une surface de 1 cm², par seconde, et par Angstroms au-dessus de l'atmosphère terrestre.

Notre télescope Celestron 11 a un diamètre de D=28 cm et une obstruction centrale de 0,357. On calcule facilement avec ces paramètres que la surface collectrice est de S = 537 cm² (S = p x 28² / 4 x (1 - 0,357) = 537 cm²).

Le nombre de photons collectés par la pupille est donc : N1 =S x N = 537 x 2,79 x 10¹¹ = 1,50 x 10¹⁴ photons/s/A.

Autour de la longueur d'onde de 5550 A, le spectre Alpy 600 est échantillonné par les pixels de la caméra au pas de 4,914 A/pixel (en mode binning 2x2).

Astuce : comment trouver cette valeur d'échantillonnage ? Depuis la ligne de commande ISIS, lancez la commande suivante (il n'y a pas de paramètres) :

>DISPERSION

Cette fonction génère dans le répertoire de travail un fichier DISPERSION.LST contenant la valeur de la dispersion spectrale en fonction de la longueur d'onde (ISIS se sert pour cela de l'équation de dispersion que vous avez calculée au préalable pour traiter les spectres). Voici un extrait de ce fichier :

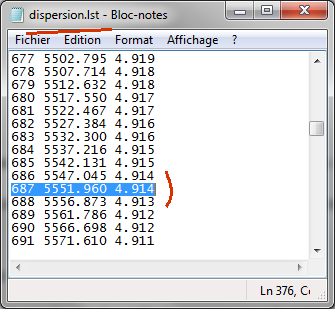
La première colonne est le numéro du pixel suivant l'axe de dispersion (en coordonnée détecteur), la seconde, la longueur d'onde associé et la troisième est la dispersion réciproque en A/pixel. On retrouve bien la valeur de 4,914 A/pixel annoncée.

Dans l'intervalle spectral correspondant à un échantillon spectral, le nombre de photons incidents toutes les secondes est donc :

N2 = 4,914 x N1 = 4,914 x 1,50 x 10¹⁴ = 7,37 x 10¹⁴ photons/s

Pour un temps d'intégration t, compté en secondes, le nombre de photons sera N3 = t x N2. Comme ici le temps d'observation de référence est de t = 1 seconde, nous avons N3 = t x N2 = 7,37 x 10¹⁴ photons.

La transmission optique du télescope associé à un réducteur de focale est évaluée à 0,85. Cette valeur est le résultat du produit de la transmission de la lame de fermeture, du coefficient de réflexion de deux miroirs (traitement StarBrigth) et des lentilles du réducteur.

Le flux photonique arrivant à l'entrée de la fente du spectrographe est donc N4 = 0,85 x N3 = 0,85 x 7,37 x 10¹⁴ = 6,26 x 10¹⁴ photons.

Pour le moment on considère que la transmission optique du spectrographe est de 1 (donc, un spectrographe parfaitement transparent à la lumière). En faisant cette hypothèse, c'est donc le flux photonique N4 qui atteint le détecteur.

Connaissant le rendement quantique du détecteur à 5550 A, on calcule facilement le signal en photoélectrons par seconde. Le rendement quantique approximatif du CCD qui équipe la caméra Atik460EX (un Sony ICX694EX) est donné ici. On adopte la valeur QE = 0,76 valable autour de 5550 A.

Le nombre de photoélectrons pour notre densité de flux incident est donc N5 = QE x N4 = 0,76 x 6,26 x 10¹⁴ = 4,76 x 10¹⁴ électrons.

Dans cette même page, donnée en référence ci-devant, on trouve que le gain électronique de la caméra Atik460EX est de G = 0,260 électron/ADU. Donc, le signal attendu (ou calculé) en nombre de comptes est :

Sc = N5 / G = 4,76 x 10¹⁴ / 0,260 = 1,83 x 10¹⁵ (ADU)/(erg)

Ce résultat est à comparer au signal effectivement observé So = 5,39 x 10¹⁴ (ADU)/(erg).

Nous expliquons l'écart par le rendement proprement dit du spectrographe Alpy 600 (sa transmission optique), que nous n'avons pas considéré jusqu'alors. Ce rendement est donné par le ratio Rs = So / Sc, soit Rs = 5,39 x 10¹⁴ / 1,83 x 10¹⁵ = 0,29.

Ce coefficient de transmission est une caractéristique importante de l'instrument. Bien sûr, plus le résultat est proche de 1, meilleur est le rendement du spectrographe. Je vous invite à réaliser ce calcul et à calculer par vous-même le rendement de votre propre instrument.

Dans le cas présent, Rs est égal au produit de la transmission des deux faces de la fente en verre sérigraphié, de deux objectifs, de l'élément dispersif (un grism) et du hublot d'entrée de la caméra CCD. Le seeing n'impacte pas ici le résultat, car ici l'observation est faite avec une fente large, bien plus large que le disque de seeing (c'est de cette manière qu'a été relevé la courbe se sensibilité, avec une fente de 230 microns). Si vous travaillez avec une fente étroite, le rendement peu chuter d'un bon facteur 2 suivant le seeing, la qualité du guidage, la largeur proprement dite de la fente, ... Ces pertes dans l'ouverture de la fente sont à comptabiliser dans le calcul de Rs.

Vous avez à présent tous les éléments pour évaluer le signal attendu d'une étoile quelconque. En fonction de la magnitude de l'étoile, vous calculez sont flux énergétique en ergs/cm²/s/A (pour une longueur d'onde de votre choix). Vous multipliez ce résultat par la bande passante spectrale d'un échantillon spectral, par la transmission atmosphérique, par la surface du télescope, par la transmission optique du télescope et par la transmission optique du spectrographe (faite une estimation expérimentale de ce paramètre au préalable, comme cela vient d'être expliqué). Convertissez ensuite le flux en nombre de photons, puis en électrons à partir du rendement quantique. Le nombre de comptes numériques recherché est enfin donné en utilisant le gain de la caméra. Bien sûr, si le temps de pose est différent de 1 seconde, vous multipliez ce résultat par le temps de pose en secondes.

Note : attention au piège sur le temps d'intégration avec certaines caméras et/ou logiciel d'acquisition. Ainsi dans l'exemple, le temps d'intégration affiché lors de l'observation de l'étoile HD196544 était de 2,30 secondes. Mais un test simple montre que ce n'est pas le vrai temps de pose, car le logiciel interne de la caméra ou du logiciel produit une erreur d'arrondie. Il est facile de s'en apercevoir en faisant une pose de 23 secondes (23 = 10 x 2,3). L'anomalie existe si le signal enregistré n'est pas précisément 10 fois supérieur. Dans le cas contraire, il faut corriger le temps de pose (la valeur fiable correspond au long temps de pose long, car les erreurs d'arrondi sur les valeurs fractionnaires sont largement réduites). Dans notre exemple, il s'avère que le temps de pose effectif n'est pas de 2,30 secondes, mais de 2,49 secondes ! Soit donc une erreur de 8% environ, soit encore 0,086 magnitude, ce qui n'est pas du tout négligeable lorsqu'on cherche à réaliser des mesures spectrophotométriques précises. Pour éviter ce genre de désagrément, j'essaye toujours (si le temps de d'intégration est bref)  d'observer l'étoile cible et l'étoile de comparaison avec le même temps durée d'exposition. 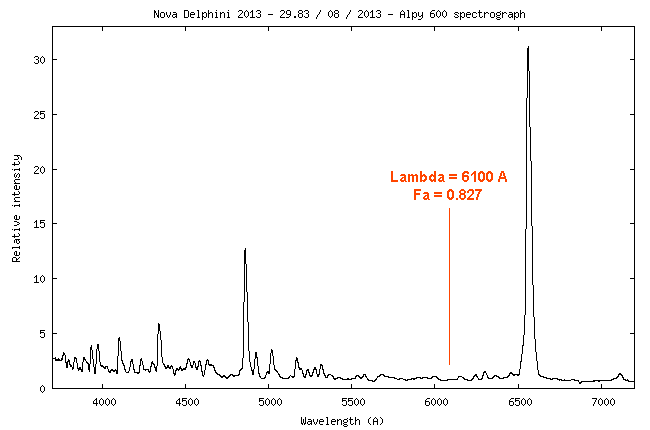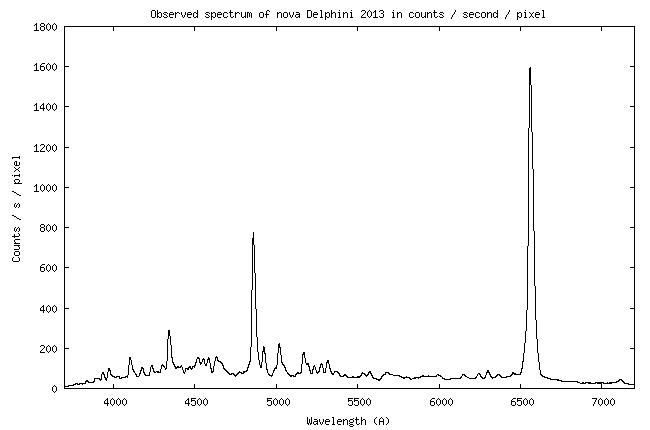C'est l'origine du temps de pose affiché de 2,30 secondes, qui peut paraître étrange. En fait, cette durée a été fixée lors de l'observation de la nova Delphini 2013 (notre cible) pour ne saturer aucun point du spectre avec l'équipement décrit, tout en ayant un signal élevé. Du coup, j'ai adopté ce même temps d'exposition pour la référence (l'étoile HD196544) pour échapper à tout problème (même si dans ces conditions, le spectre de létoile de référence est sous-exposé – pour compenser, j'ai cumulé un grand nombre d’images).