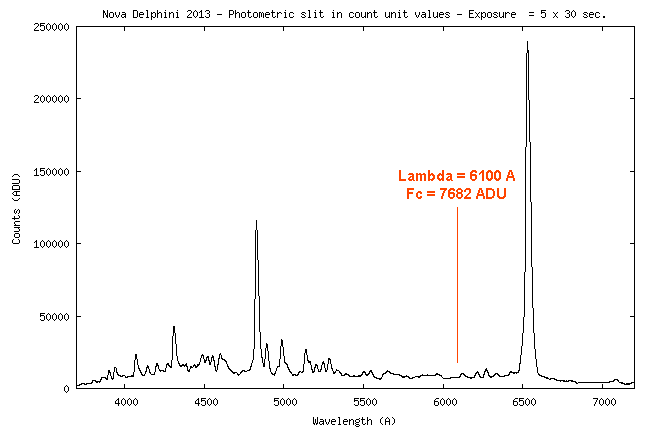
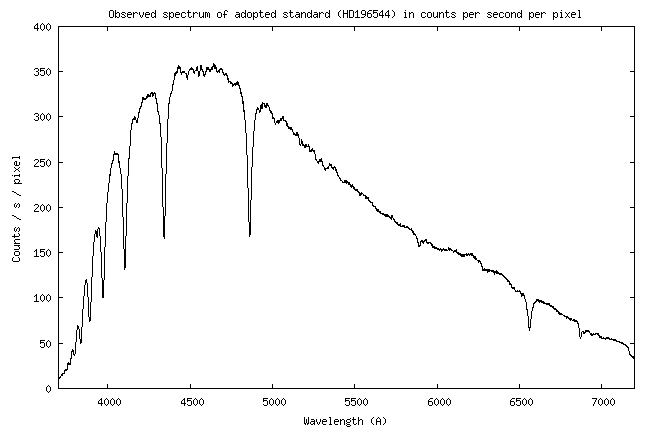
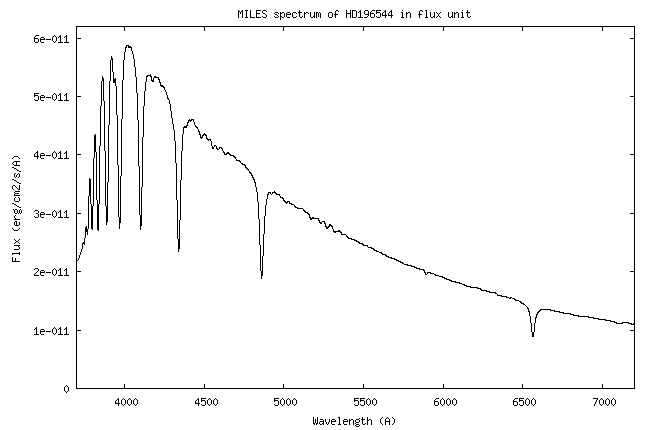
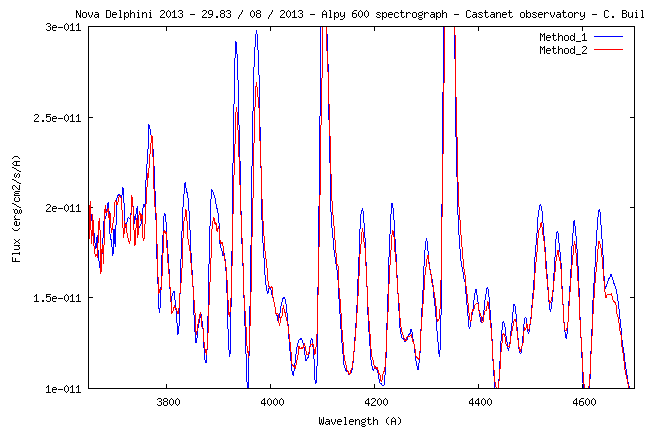
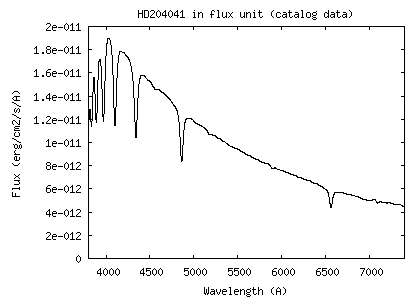
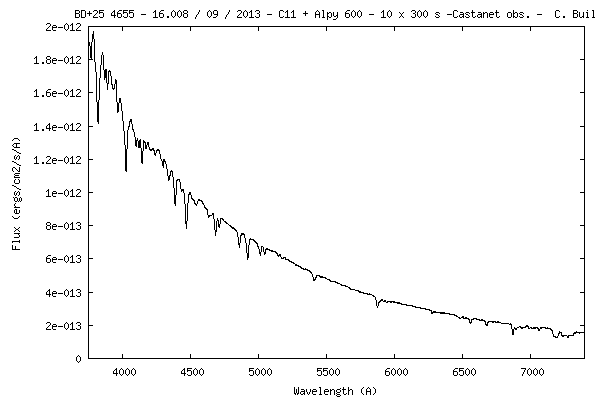
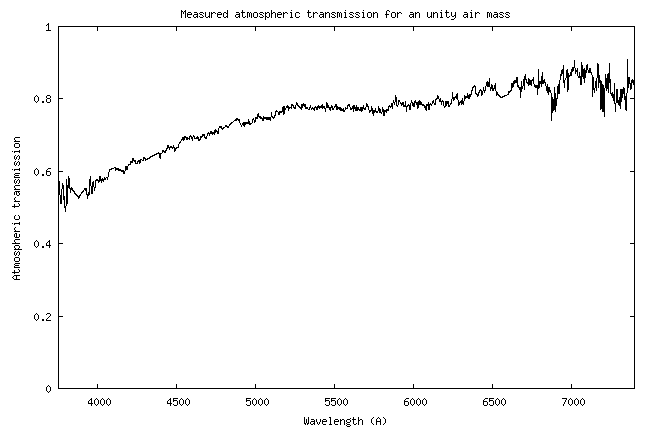
| We describe here
the workflow for predicting the measured number of digital counts in spectrum
chosen point of the signal for a given
star given.
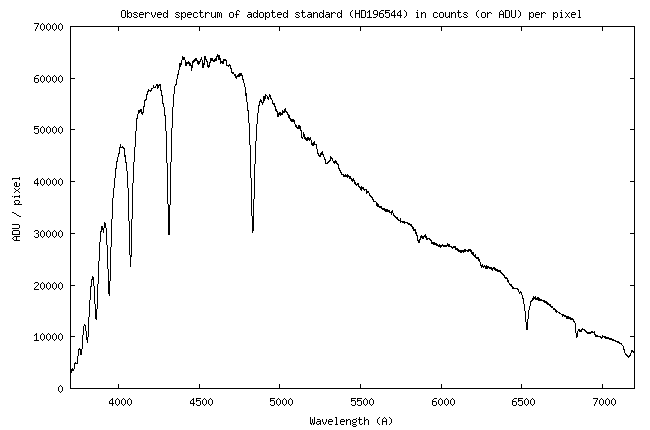
For this demonstration I will be using the instrumental
system sensitivity curve established during the observation of star HD196544, while it was
at an elevation of 57.08 ° above the horizon
(an air mass of
1.191). During the night of observation in question, the atmosphere was very pure. the AOD
(Aerosol Optical Depth) was measured at 0.09 from the observation of two stars at different elevations (see section 4).
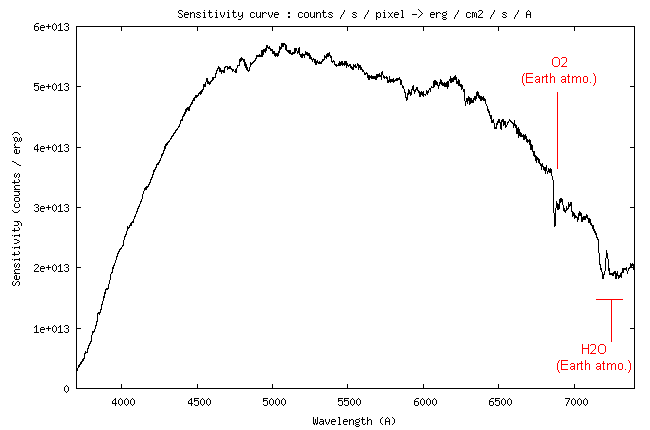
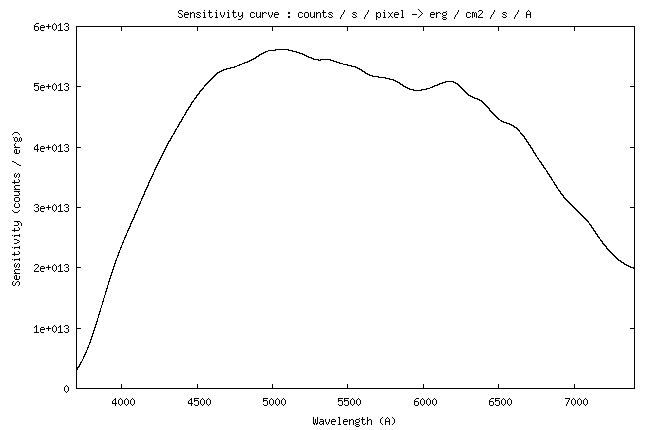
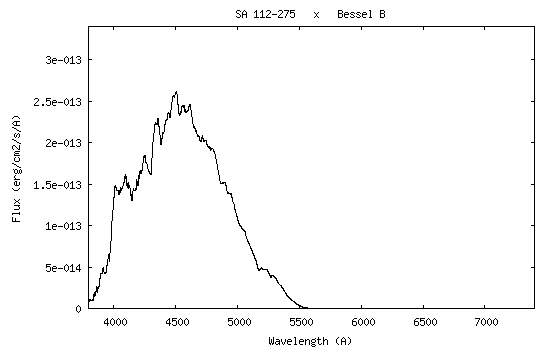
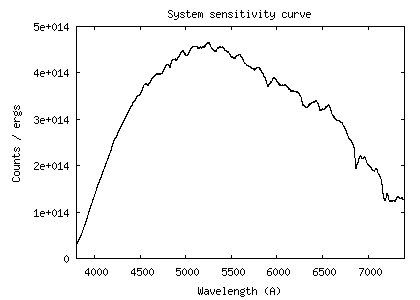
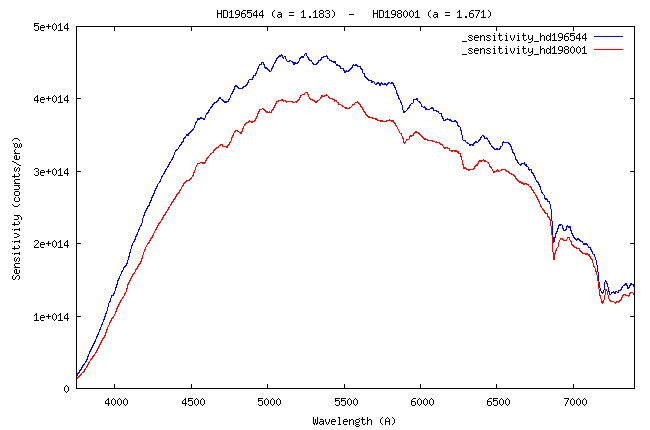
Here the sensitivity curve:

I remember that this curve is the link between the digital counts (the
signal inADU = Analog
Digital Unit) observed in a sample of the spectrum (after of
course removing the offset signal, the thermal
signal and the sky background) and a
flux of 1 erg/cm2/s/A
at the telescope entrance for the given wavelength (see Part 1,
Method 2). The sensitivity is reduced to an exposure time of 1 second.
The telescope is a Celestron 11,
the spectrograph is an Alpy 600
and the camera amodel Atik460EX operated binning
2x2. I arbitrarily select to perform the calculation at
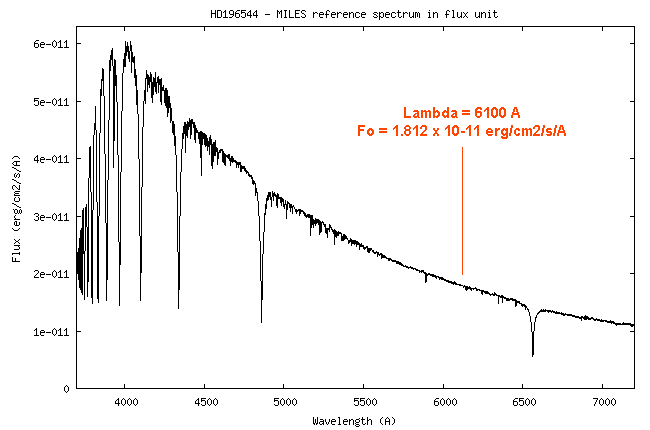
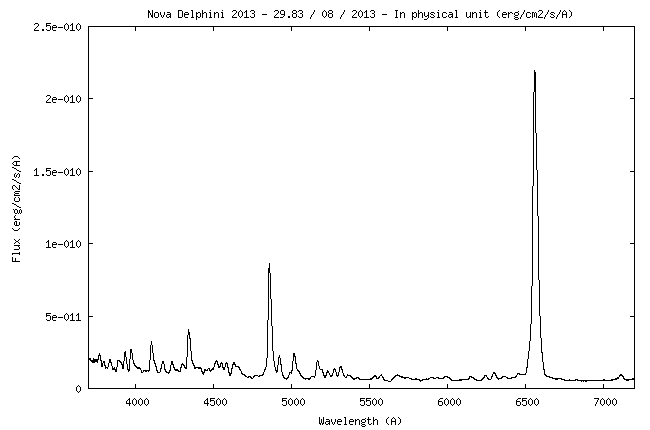
the wavelength of 5550 A. Of course, you can select any other point of the spectrum.
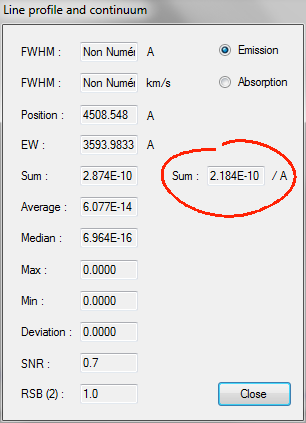
At the wavelength of 5550 A, the value of the instrumental sensitivity is 4.26 x 1014 (ADU)/(erg) - see the curve.
We will calculate the number of ADU that would be measured
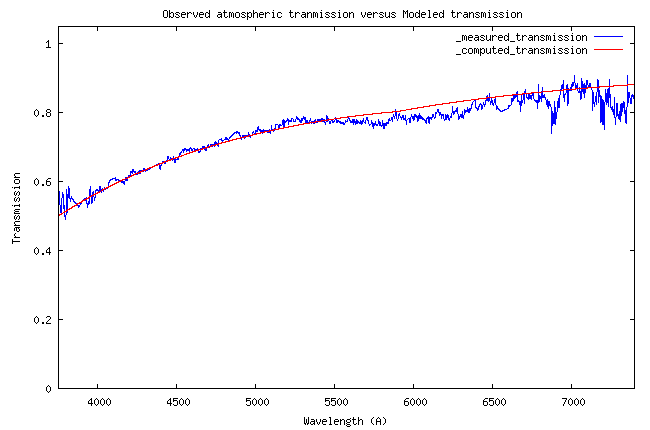
if the instrument was located outside the Earth's atmosphere. Atmospheric transmission is calculated
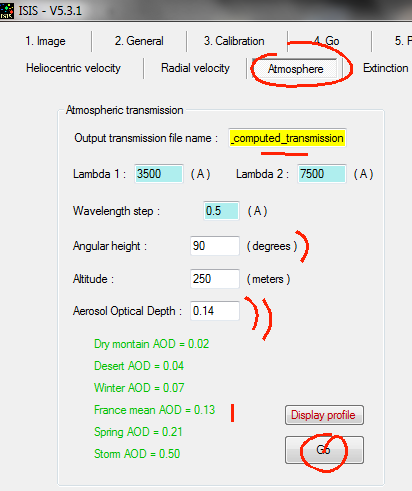
by using "Miscellaneous" tab
and "Atmosphere" tool for a star elevation of H = 57.08° and AOD = 0.09.
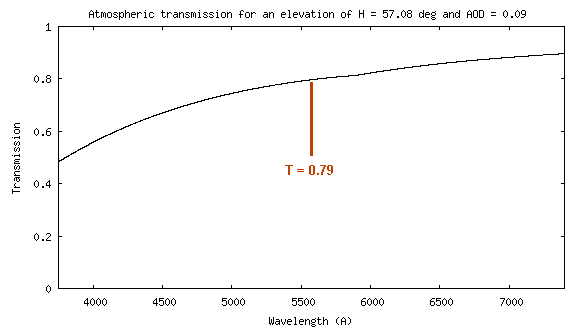
The observed signal outside the atmosphere would be: So = 4.26 x 1014 / 0.79 = 5.39 x 1014 (ADU)/(erg). This is the value that we will try to find by calculation.
This means a star outside the atmosphere producing a flux Fo = 1 erg/cm2/s/A.
For convenience, this energy
flux is converted into a photons
flux (photons/cm2/s/A).
The conversion formula between the flux expressed in ergs and the flux expressed in photons
is
No = (Fo x W) / (1.9861 x 10-8)
with the wavelength in Angstroms.
Doing the
numerical application:
:No = (1 x 5550) / (1.9861 x 10-8) = 2.79 x 1011 photons/cm2/s/A
This is exactly the number of photons received from our star in an area of
1 cm2, per second,
per one angstroms bandwith
above the Earth's atmosphere.
Our Celestron 11 has a diameter of D = 28 cm and a central obstruction of 0.357. Is easily to
calculate the collecting surface with these parameters:
S = 537 cm2 (S = p
x 282
/
4 x (1
- 0.357) = 537 cm2).
The number of photons collected by the telescope
pupil is: N1 = S x N = 537 x 2.79 x 1011 = 1.50 x 1014 photons/s/A.
Around the wavelength 5550 A, the Alpy 600 spectrum is sampled by the camera
pixels with a pitch of
4.914 A/pixel
(in bin 2x2 mode).
Tip: how to find this sample value? From the ISIS
command line, run the following command (there are no parameters):
>DISPERSION
This function generates in
the working directory a
DISPERSION.LST file containing the value of the spectral dispersion as a function of wavelength (ISIS
uses for this
the dispersion equation you calculated previously for
process the spectra). Here is an excerpt of this file:
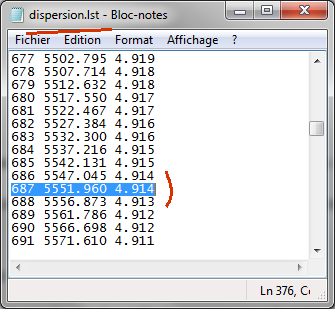
The first column is the
pixel number along the axis of dispersion axis
(as a detector coordinate), the second is
the associated wavelength,
the third is
the reciprocal dispersion in A/pixel. We recover the value of 4.914 A/pixel announced.
In the spectral interval corresponding to a spectral sample, the number of incident photons every second is:
N2 = 4.914 x N1 = 4.914 x 1.50 x 1014 = 7.37 x 1014 photons/s
For an integration time t, counted in seconds, the number of photons will N3
= t x N2. Here,
the reference time
observation is t = 1 second,
so
N3 =
t x N2 = 7.37 x 1014 photons.
The optical transmission associated with the
telescope and focal
reducer is evaluated
to 0.85. This value is the result of the product of the transmission of the entrance
plate, the reflection coefficient of both mirrors (StarBrigth) and transmission
of the focal
reducer lenses.
The photon flux arriving at the entrance
slit is N4 = 0.85 x
N3 = 0.85 x 7.37 x 1014 =
6.26 x 1014 photons.
For the moment we consider that the optical transmission of the spectrograph is 1 (ie, perfectly transparent to light). In making this
hypothesis, the
N4 photon flux reaches the detector.
Knowing the quantum efficiency of the detector at 5550 A, the optical
signal is easily converted
in photoelectrons per second. The approximate CCD
quantum efficicency of
Atik460EX camera (Sony ICX694EX) is given here. Value adopted
is QE = 0.76
around 5550 A wavelength.
The number of photoelectrons for our incident flux density is N5 = QE
x N4 = 0.76 x 6.26 x 1014 =
4.76 x 1014 electrons.
In this same page, given with reference to above, we find that the electronic
gain of Atik460EX camera
is G = 0.260 electron/ADU. So, the expected signal (or
calculated) in
counts number is
Sc = N5 / G = 4.76 x 1014
/ 0,.260 = 1.83 x 1015 (ADU)/(erg)
This result is compared to the signal actually observed,
So = 5.39 x 1014 (ADU)/(erg) .
We explain the difference in the actual efficency
of Alpy 600 spectrograph (its optical transmission), we have not seen before. This
efficency is given by the ratio
Rs = So / Sc, so Rs = 5.39 x 1014 / 1.83 x 1015 = 0.29
This transmission coefficient is an important feature of the instrument. Of course, the more the result is close to 1, the better is
the spectrograph efficiency. I invite you to make this calculation and calculate for yourself the performance of your own instrument.
In the
present situation, Rs is equal to the product of the transmission of both sides of the slit
parallel plate, two objective lenses, the dispersive element (a grism) and
the entrance window of CCD camera. The seeing does not impact here
the result, because here the observation is made with a wide slit, much larger than the seeing disk
(a
230 microns slit). If you work with a narrow slit, the performance can
drop be a factor 2 for
example, because presence of seeing and guidance errors (function
of slit width). These losses at
the slit level are to be recognized in the calculation of Rs.
You now have all the elements to evaluate the expected signal produced
in the spectrum for any star. Depending on the magnitude of the star, you calculate flux
energy in ergs/cm2/s/A (for a wavelength of your choice). You multiply this result by the spectral sample bandwidth, by
atmospheric transmission, by the surface of the telescope, by
the optical transmission of the telescope and the optical transmission of the spectrograph (made a
experimental estimate of this parameter in advance, as just explained). Then, convert the flux number of photons into
electrons by using detector quantun efficiency. Finally,
the
ADU number is given by the camera electronic
gain. Of course, if the exposure time is
not equal to 1 second, you multiply the result by the exposure time in seconds.
Note: Be careful with
the integration time with some cameras and/or acquisition software. Thus in the example, the consigned
integration time when observing the star HD196544 was 2.30 seconds. But a simple test shows that this is not the true exposure time because the internal camera software or
acquisition software generate
a rounding error. It is easy to notice by making
a 23 seconds exposure (23 = 10 x 2.3). The anomaly exists if the recorded signal is not
precisely 10 times. Otherwise, you must correct the exposure time (reliable value is the long long exposure, because rounding
potentiel
error effect is greatly reduced). In our example, it turns out that the effective exposure
time is not 2.30 seconds, but 2.49 seconds ! The
error is about 8%, or
0,086 magnitude, which is not negligible when trying to perform accurate spectrophotometric measurements. To prevent this, I always try (if
the exposure time is short) to observe the target star and the comparison star with the same integration
time. This is the origin of the 2.30
seconds exposure for HD196544, which may seem strange. In fact , this duration has been fixed during the observation of the nova Delphini
2013 (our target) will not
saturate any part of the spectrum with the equipment described. So, I adopted the same exposure time for
reference (HD196544 ) to avoid any problems (although in these conditions, the refrence
spectrum is underexposed - to compensate I have accumulated a large number of images).
|