Introduction
aux méthodes spectrophotométriques
Comment
trouver la transmission d'un filtre, comment évaluer le rendement
d'un spectrographe,
comment calculer le rendement quantique
d'un détecteur et plus encore !
Cette page contient un recueil de techniques ayant trait à la spectrophotométrie. Vous allez ainsi apprendre à mesurer la transmission optique d'un filtre interférométrique, à graduer en spectre en unités physiques, à rattacher les données dans un système BVRI, ...
Pour rendre tout ceci possible avec une bonne précision, il est quasi obligatoire de travailler avec un spectrographe dont la fente est large comparativement u disque de seeing atmosphérique et comparativement à l'amplitude de l'erreur de guidage lors des poses. C'est le seul moyen d'avoir la garantie que le flux collecté par le télescope arrive sur le détecteur en même quantité, quel que soit le spectre acquis d'un même objet. Avec un spectrographe LISA par exemple, il est vivement recommandé d'utiliser une fente de 50 microns, ou mieux 100 microns de large (disponible auprès de la société Shelyak). Autre exemple, pour le spectrographe Alpy 600, une bonne idée est d'utiliser la fente spéciale "photométrie", dont les caractéristiques sont décrites ici.
Sommaire :
La
mesure de la transmission d'un filtre coloré
La
mesure du rendement optique d'un spectrographe
La
mesure du rendement quantique d'un capteur CCD
Le
rattachement des spectres à des unités physiques
Comment
évaluer la magnitude vraie d'une étoile
Comment
convertir le signal observé dans un système photométrie
Comment
trouver la température photosphérique d'une étoile
Comment
convertir l'intensité des spectres en flux absolu par la pratique
Annexe
: une liste de standards spectrophotométriques
1. La mesure de la transmission d'un filtre coloré
Nous allons relever la courbe de transmission spectrale d'un filtre interférentiel à partir de l'observation de spectres d'une étoile. Le spectrographe utilisé pour cette démonstration est le modèle Alpy 600 de la société Shelyak Inst.
L'étoile sélectionnée est un standard spectrophotométrique extrait d'une liste spécialement établie pour l'étalonnage des instruments scientifiques spatiaux (initialement le Hubble Space Telescope) et des spectrographes exploités dans des observatoires sol professionnels. C'est la base CALSPEC. Une sélection est donnée en annexe sous forme d'une liste.
Le spectre de l'étoile BD+25 4655 extrait de la base CALSPEC Cet objet va servir de fil conducteur pour la suite :
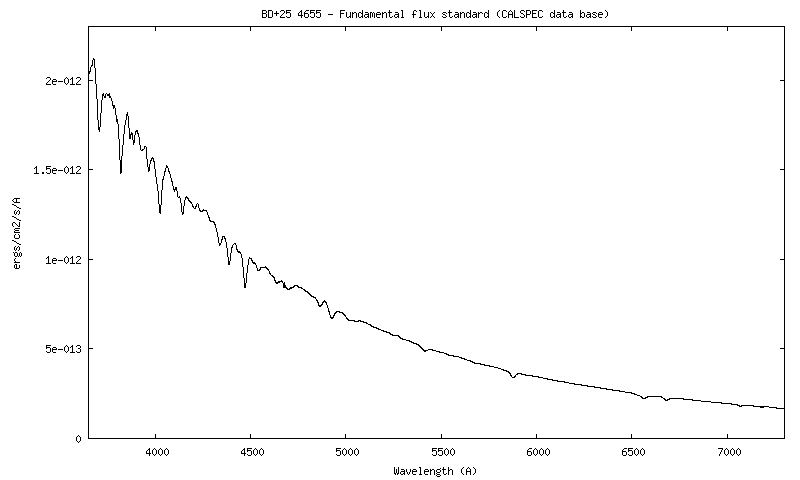
Spectre
en flux absolu (ergs/cm2/s/A) de l'étoile BD+25 4655 (CALSPEC)
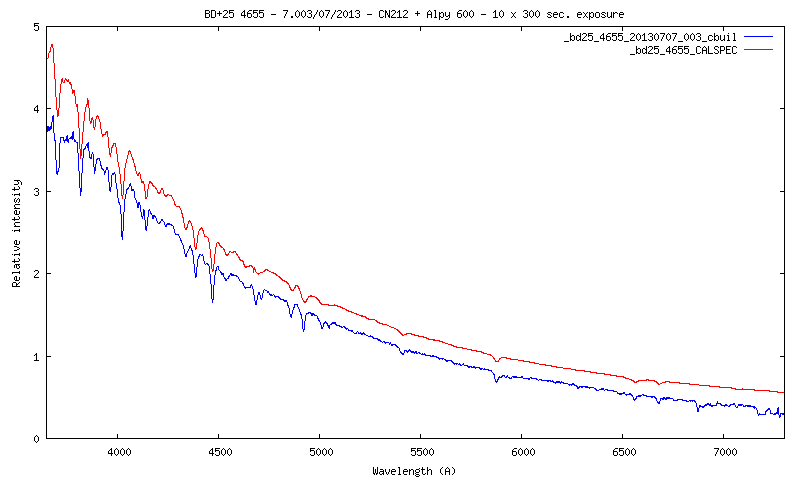
|
En bleu, le spectre de BD+25 4655 réalisé avec un spectrographe Alpy 600 monté au foyer Newton d'un télescope CN212 (D=21.2 cm, F/4). La caméra est un modèle Atik460EX exploitée en binning 2x2. Fente de 18 microns de large (pour un pouvoir de résolution de R=700 environ). Temps de pose = 10 x 300 sec. En rouge, le spectre CALSPEC de cette même étoile (ce spectre est décalé de 0,2 unité suivant l'axe de intensité pour clarifier le graphique). |
On remarque dans cet exemple la grande similitude entre le spectre observé et le spectre attendu. La résolution spectrale est supérieure dans le spectre Alpy 600, mais ce n'est pas le paramètre important ici. Le spectre Alpy 600 montre aussi un signal cohérent jusqu'à 4650 A, donc très loin dans l'ultraviolet. Ce résultat remarquable peut être mis en évidence car BD+25 4655 émet un fort flux dans l'ultraviolet. De fait, le profil de cette étoile n'est vraiment pas classique : c'est celui d'une naine blanche.
Voici l'image du spectrale 2D de BD+25 4655 réalisé en mode fente large (en utilisant la dual-fente 18/180 microns proposée par Shelyak pour le spectrographe Alpy 600 - voir ici pour plus de détails) :

|
Le spectre 2D de BD+25 4655. Télescope CN212, spectrographe Alpy 600 et pose de 2 x 300 secondes. On utilise la fente de 180 microns de large du dispositif spectrophotométrique Alpy 600. On est sur de cette manière qu'aucun photons n'est perdu à cause du seeing ou des erreurs de guidage durant la pose. |
L'image suivante est réalisée dans les mêmes conditions, à ceci près qu'un filtre interférentiel [OIII] Astronomik est placé juste à l'avant du spectrographe. Le signal spectral observé est donc la partie non bloquée par le filtre (partie bleu-verte du spectre). Le temps de passage entre une configuration sans filtre et avec filtre est bref pour que la variation d'extinction de la transmission atmophérique soit considérée comme négligeable :

|
Spectre 2D de BD+25 4655 observé au travers d'un filtre [OIII] Astronomik proposé pour la photographie astronomique en bande étroite. Un filtre IR-cut (IR_block Astronomik) est ajouté pour être sur de bien d'elliminer toute trace de rayonnement infrarouge lointain. Temps de pose est de 2 x 300 secondes. |
Le même travail est réalisé avec un filtre isolant les raies nébulaires [SII] (dans le rouge du spectre) :

|
Spectre
2D de BD+25 4655 observé au travers d'un filtre [SII]
Astronomik+ un filtre IR-cut. |


A
gauche, la caméra Atik460EX non équipé du filtre à mesurer. A droite,
le filtre est mise en place.
Le rapport entre le spectre réalisé au travers du filtre et sans filtre donne immédiatement la courbe de transmission des filtres. Voici le résultat :
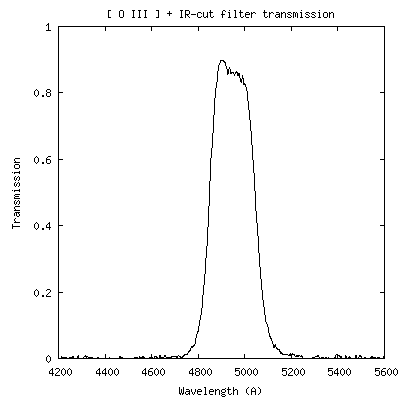
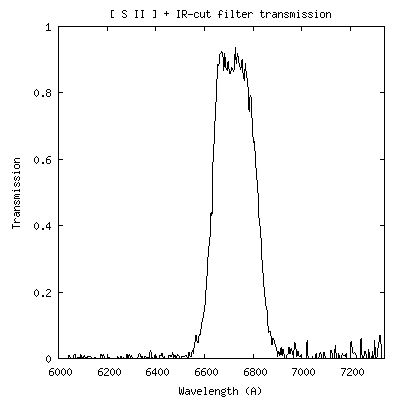
Courbes de transmission spectrale des filtres [OIII] et S[II].
Les paramètres qui caractérisent ces filtres sont :
|
|
Filtre [OIII] + IR-cut |
Filtre [SII] + IR-cut |
|
Longeur d'onde centrale |
4950 A |
6720 A |
|
FWHM |
205 A |
190 A |
|
Transmission optique |
0,87 |
0,89 |
En étant soigneux au
moment de l'acquisition (utilisation d'une fente large de 100 microns
ou plus, ou encore d'une fente dédiée comme la fente photométrique
Alpy 600), il est possible de mesurer avec précision la largeur
de nos filtres spectraux. La source de lumière utilisée est originale
: c'est celle des étoiles. Elle vient donc de loin ! L'objet observé
ici est de faible éclat (V=9,7), ce qui ajoute de la difficulté.
Vous allez obtenir un résultat plus précis encore (bien moins de
bruit de mesure) en sélectionnant une étoile plus brillante (de
magnitude 4 à 5), si possible de type BIII (raies de Balmer étant
alors étroites et assez discrètes, avec un continuum bien lisse).
2. La mesure du rendement optique d'un spectrographe
L'analyse de l'instrument peut être poussée plus avant en comparant le signal observé dans le spectre en utilisant un filtre interférentiel (ici [OIII] et [SII]) et le signal observé en plaçant la caméra CCD directement au foyer du télescope, équipée des mêmes filtres. Le rapport de ces deux signaux donne directement le rendement optique du spectrographe, c'est-à-dire la transmission optique globale depuis la fente jusqu'à l'interface avec le détecteur (elle inclue la transmission de la fente, de l'optique collimatrice, du réseau, et de l'objectif de caméra).

Le champ de l'étoile BD+25 4655 observé au foyer Newton du télescope CN212 (caméra Atik 460EX, 3 x 20 sec.)
Voici par exemple une des images utilisée pour mesurer le signal au foyer du télescope au travers du filtre [OIII] :
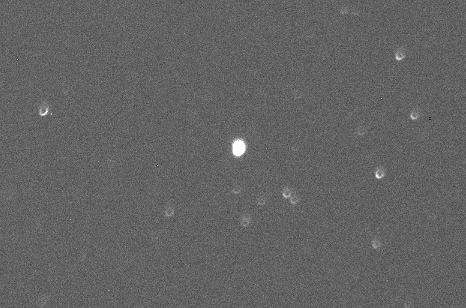
Image du champ de BD+25 4655 pour les mesures photométriques.
Les images sont volontairement défocalisées pour annuler le bruit spatial induit par la structure matricielle du détecteur. Ceci permet aussi d'allonger le temps d'intégration afin de réduire le bruit de scintillation atmosphérique (le temps de pose est de 60 secondes).
Le signal en pas codeur, ou compte numériques (ou encore ADU, pour Analog Digital Unit), est mesuré en utilisant la technique de la photométrie d'ouverture numérique (le fond de ciel est retiré automatiquement). J'ai utilisé pour celà les fonctions de photométrie du logiciel IRIS. Plusieurs clichés ont été exploités pour faire des moyennes (la dispersion des mesures est de 1% à 2% seulement).
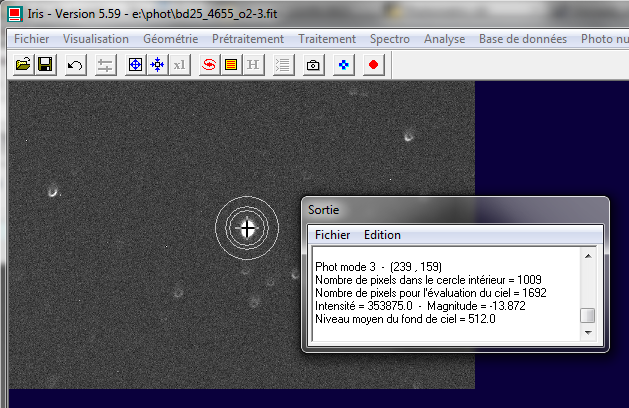
Mesure
du flux stellaire par la technique de la photométrie d'ouverture
sous le logiciel IRIS.
Pour pouvoir comparer
le signal observé dans les configurations instrumentales testées,
il est important de tenir compte de la transmission atmosphérique
car celle-ci modifie la quantité de signal reçu de l'objet en
fonction de son élévation au dessus de l'horizon. Pour la nuit d'observation
considérée, la transmission atmosphérique a été mesurée. Elle est
de T = 0,77 à 5000 A au zénith (masse d'air de a = 1) et de
T
= 0,86 à 6720 A (toujours au zénith).
Le signal mesuré est ramené à ce qu'il serait si l'étoile était au zénith et pour un temps de pose de 1 seconde. Voici le détail du calcul pour l'observation de BD+25 4655 avec un télescope CN-212 :
|
|
Filtre [O III] (4950 A) |
Filtre [S II] (6720 A) |
|
Date |
6.942/07/2013 |
6.935/07/2013 |
|
(1) Signal mesuré en 60 sec. pour la date |
631000 ADU |
274000 ADU |
|
(2) Temps d'intégration |
60 sec. |
60 sec. |
|
Masse d'air (a) |
1.695 |
1.765 |
|
(3) Extinction pour
la masse d'air d'observation |
0.642 |
0.781 |
|
Signal pour une masse
d'air unitaire (zénith) et pour un temps de pose de
1 seconde |
16380 ADU/s pour a = 1.0 |
5850 ADU/s pour a = 1.0 |
Le même travail de mesure du signal intégré dans la bande spectrale des filtres est réalisé dans les images spectrales produites par le spectrographe Alpy 600. Voici l'image de BD+25 4655 dans la caméra de guidage (une Atik 314L0+) - juste à gauche de la fente. La structure duale de cette dernière est bien visible (18/180 microns) car le fond de ciel est rendu très lumineux par une forte pollution lumineuse :

Le champ de BD+25 4655 saisi par la caméra de guidage Alpy 600.

Le
montage du filtre interférentien passe-bande à l'avant d'un spectrographe
Alpy 600.
Il suffit pour cela de relever le nombre de comptes numériques dans les images 2D du spectre. Par exemple sous ISIS :
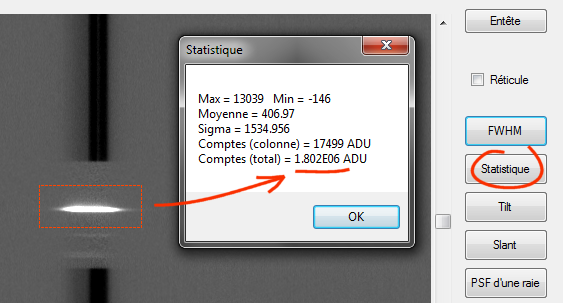
Voici le résutat des données mesurées dans les spectres :
|
|
Filtre [O III] (4950 A) |
Filtre [S II] (6720 A) |
|
Date |
6.996/07/2013 |
6.935/07/2013 |
|
Signal mesuré en 60 sec. pour la date |
9.00 x 105 ADU |
1.83 x 105 ADU |
|
Temps d'intégration |
300 sec. |
300 sec. |
|
Masse d'air (a) |
1.483 |
1.440 |
|
Extinction pour la masse d'air d'observation |
0.640 |
0.805 |
|
Signal pour une masse d'air unitaire (zénith) et pour un temps de pose de 1 seconde. |
4690 ADU/s pour a = 1.0 |
760 ADU/s pour a = 1.0 |
Le rendement optique global spectographe Alpy 600 vers 5000 A est donc de 4690 / 17500 = 0.268 (on peut arrondir à 27%).
Ce même rendement vers 6700 A est évalué à 760 / 5850 = 0.130 (soit 13%).
Toujours en exploitant
le signal des étoiles, on décrit une méthode simple pour évaluer
le rendement optique d'un spectrographe. Il suffit de ce munir de
filtres interférentiels courant pour isoler une bande passante relativement
étroite. L'usage d'une fente large photométrique s'avère ici encore
déterminant. Notez qu'on réalise ici des mesures photométriques
assez pointue. Enfin, ne jamais oublier qu'en matière de mesure
photométriques de ce type, la marge d'erreur est toujours élevée,
typiquement comprise entre 10 et 20%.
3. La mesure du rendement quantique d'un capteur CCD
Le rendement quantique est le rapport entre le nombres de photoélectrons provoqués par la flux stellaire incident et le nombre de photoélectrons mesurés dans son image électronique.
On va d'abord évaluer le nombre de d'électrons sensés êtres produit notre étoile cible.
D'après les données HST (voir le profil en flux au début de cette page) nous reçevons de l'étoile BD+25 4566 au dessus de l'atmosphère terrestre un flux énergétique de 7.05 x 10-13 ergs/cm2/s/A à 4950 A et de 2.25 x 10-13 ergs/cm2/s/A.
Il est facile de transformer ce flux énergétique en un flux de photons avec l'équation :
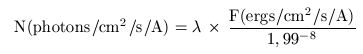
avec la longueur d'onde en angstroms.
Voici l'ensemble des paramètres nécessaires au calcul :
|
|
4950 A |
6720 A |
|
Flux énergétique |
7.05 x 10-13 ergs/cm2/s/A |
2.25 x 10-13 ergs/cm2/sA |
|
(1) Flux de photons |
0.175 photons/cm2/s/A |
0.0760 photons/cm2/s/A |
|
(2) Surface collectrice (CN212) |
318 cm2 |
318 cm2 |
|
(3) Bande passante (FWHM filtre) |
205 A |
190 A |
|
(4) = (1) x (2) x (3) |
11350 photons/s |
4590 photons/s |
|
(5) Transmission atmosphérique (a = 1) |
0.77 |
0.86 |
|
(6) Transmission télescope |
0,71 |
0.67 |
|
(7) Transmission filtre |
0.87 |
0.89 |
|
(8) Transmission hublot caméra |
0,98 |
0.97 |
|
Transmission optique = (9) = (5) x (6) x (7) x 8) |
0.466 |
0.490 |
|
Flux photonique = (4) x (9) |
5190 photons/s |
2250 photons/s |
Noter la transmission optique adoptée pour le télescope, 71% à 5000 A. Elle correspond à une transmission des miroirs individuels de 84%. La valeur type pour une alluminure fraiche et de qualité est entre 85% et 86%. Ici l'alluminure n'est pas toute jeune, mais elle n'est pas du tout oxydée et ni piquée, tout juste un peu poussièreuse. Pour information, la transmission optique globale d'un télescope SCT Celestron dans une version de traitement StarBright XLT est de 86% environ vers 5000 A (ceci inclu la lame de fermeture et les deux miroirs). Cet écart de transmission a pu être vérifiée entre les deux types de télescopes sur des visées d'étoiles.
Calculons maintenant le nombre de photoélectrons observé en une seconde de pose.
Au foyer direct du télescope CN212 nous avons mesuré 16380 ADU/s pour une masse d'air unitaire (voir le paragraphe précédent) à la longueur d'onde de 4950 A et 5850 ADU/s à la longueur d'onde de 6720 A.
On converti le signal exprimé pas codeur (ADU) en un signal exprilé en électrons à partie du gain électronique de la caméra CCD. Ce dernier a été évalué par ailleurs pour le modèle Atik460EX (voir ici la méthode de calcul). Nous avons ici un gain (inverse) pour ce modèle de caméra est de 0,26 électron/ADU. On trouve au final :
|
|
4950 A |
6720 A |
|
(1) Signal mesuré en ADU |
16380 ADU/s |
5850 ADU/s |
|
(2) Gain caméra |
0.26 e-/s |
0.26 e-/s |
|
Signal mesuré en électrons = (1) x (2) |
4260 électrons/s |
1520 électrons/s |
Le rendement quantique vers 5000 A est finalement égal à 4260 / 5190 = 0,821, soit une valeur arrondie de 82%. La valeur admise pour le CCD Sony ICX694ALC qui équipe la caméra CCD Atik460EX est de 76% (voir ici). On suppose que le hublot de fermeture du composant CCD fait partie intégrante du dispositif et que le rendement quantitique inclu sa présence (les documentations et publications ne sont jamais claires sur ce point).
Le rendement quantique trouvée expérimentalement (82%) est sensiblement sur-évaluée par rapport à la valeur généralement admise (76%), soit une erreur de 7% environ. L'écart est dans la marge d'erreur de l'opération compte tenu du cumul d'hypothèses et d'incertitudes exprimentales potentielles pour arriver à ce résultat. Le résultat n'est donc pas aberrant. La principale cause d'erreur est l'instabilité de la transmission de l'atmosphère en cours de nuit où suivant l'endroit visé dans le ciel.
Pour la longueur d'onde de 6720 A, on trouve pour la valeur exprimentale du rendement quantique : 1520 / 2250 = 0,67, soit 67%. Un résultat à comparer à la valeur de 62% habituellement adoptée. Ici encore le rendement trouvé par l'observation est sur-évalué.
Il est probable qu'en moyennant 4 ou 5 mesures indépendantes, réparties sur autant de sessions d'observation (en prenant soin de bien mesurer la transmission atmopshérique lors de nuits photométriques), la marge d'erreur sera réduite.
4.
Le
rattachement des spectres à des unités physiques
Le spectre de l'étoile BD+17 4708, de magnitude V = 9.45 (référence SIMBAD) pris avec le spectrographe Alpy 600 au foyer Newton F/4 d'un télescope CN212 (D=21.2 cm) :
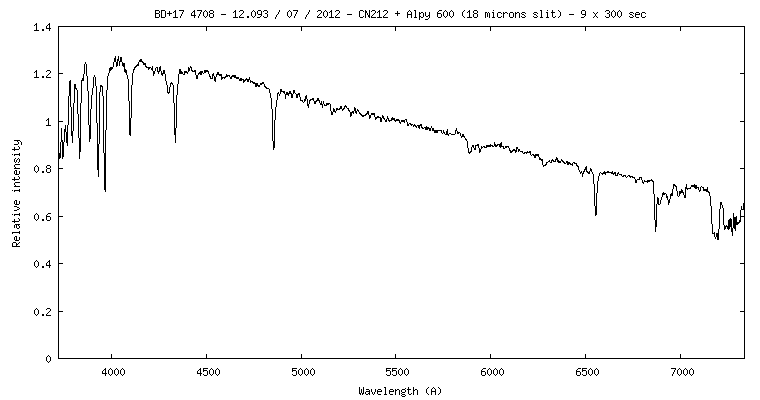
Cette étoile est un standard spectrophométrique fondamental de la base CALSPEC (voir l'annexe). Le flux est ici exprimé en unités relative - il est normalisé à l'unité autour de la longueur de 5555 A.
Connaissant la magnitude V de l'object, il est possible de calculer le profil spectral en unité de flux énergétique, en ergs/cm2/s/A, via la formule :
![]()
Vous pouvez aussi utiliser une fonction du logiciel ISIS qui exploite directement cette formule :
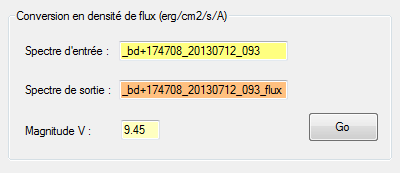
Voici le résultat en adoptant la magnitude V = 9.45, avec en comparaisons le spectre CALSPEC de cette étoile :
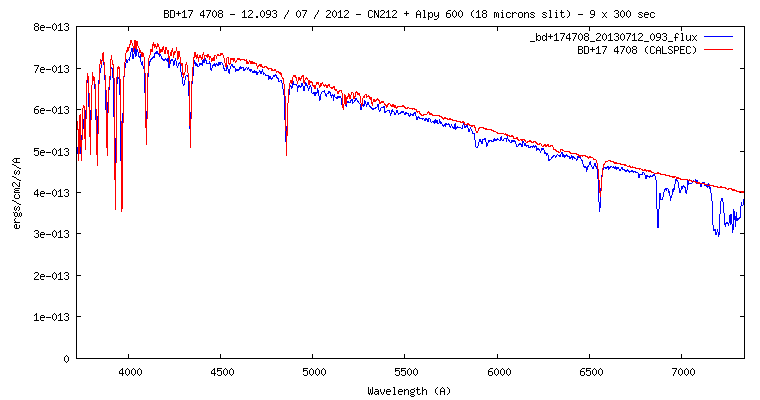
En bleu, le spectre
observé. En rouge le spectre CALSPEC).
Vous L'étalonnage en
flux absolu est un sujet de grande importance. L'enjeu de certaines analyses
astrophysiques repose sur cette mesure (pas toutes cependant, un
spectre en valeur relative garde une grande valeur pour de nombreux
travaux aussi). On trouvera dans
cette page la description pratique et détaillée de méthodes
pour arriver à étalonner en flux de manière relativement routinière
les spectres acquis.
5. Comment évaluer la magnitude vraie d'une étoile
On va utiliser la méthode classique de la photométrie différentielle pour trouver la magnitude de la cible. La référence est une étoile observée dans dans des conditions similaires et dont on connait la magnitude. Le cas traité est celui d'une obsevation de l'étoile RR Lyrae réalisée le 7 juillet 2013.
L'étoile de référence est ici HD198183 de magnitude V = 4,75. Le spectre est réduit de manière habituelle en tenant compte de l'extinction atmosphérique afin d'évaluer le flux hors atmosphère. La méthode est détaillée sur cette page : http://www.astrosurf.com/buil/isis/guide_response/method.htm.
Ci-dessous, à guche la courbe d'extinction atmosphérique au zénith utilisée pour cette étude et mesurée expérimentalement, et à droite, la courbe de réponse instrumentale adoptée :
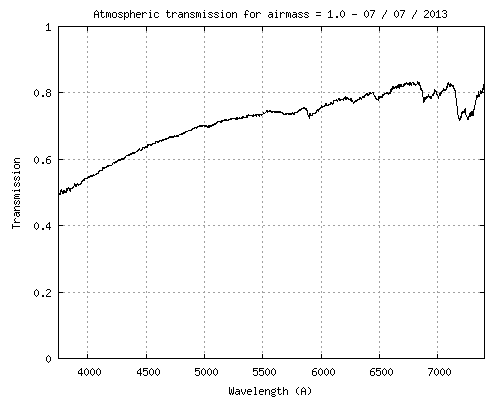
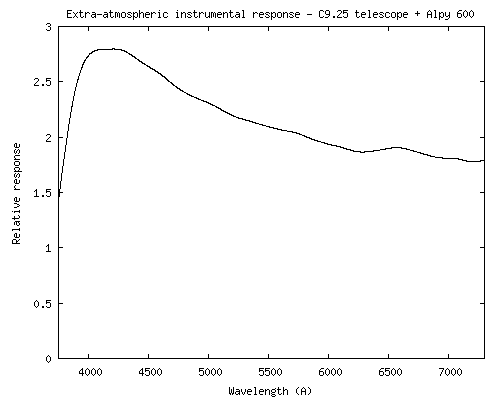
On dispose de 16 poses du spectre de l'étoile HD198183 de 16 secondes chacunes. Le signal de l'étoile est corrigé de la réponse instrumentale et de l'absorption atmopshérique :
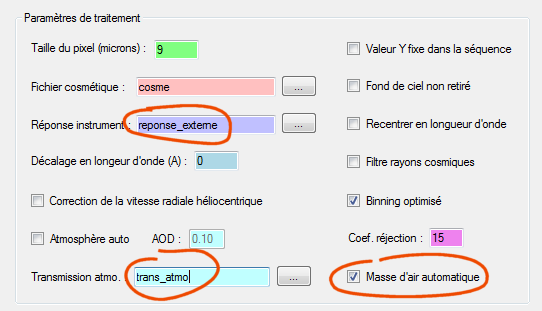
Voici le résulat en normalisant le spectre à partir de la moyenne du signal mesuré entre 5540 A et 5570 A (centre approximatif de la bande V photométrique) :
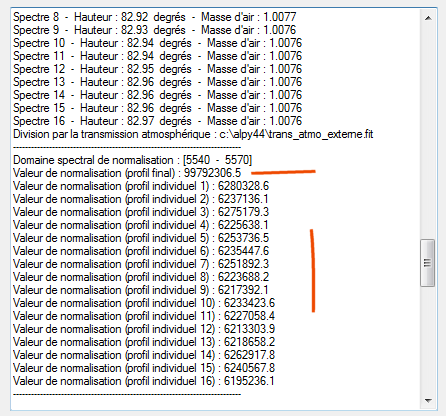
ISIS retourne une valeur de signal moyenné de 9.98 x 107 ADU dans le temps d'intégration de 16 x 16 sec = 256 sec. Soit 9.98 x 107 / 256 =3.90 x 105 ADU/s. On peut noter que le signal individuel relevé dans chacun des 16 clichés traités est très similaire. C'est une grande force de la fente photométrique. Avec une fente étroite, un tel tir groupé serait impensable à cause du seeing et des erreurs de guidage.
Le calcul est à l'identique est réalisé à l'identique sur une séquence d'images de l'étoile RR Lyrae, pour un temps de pose individuel de 300 secondes :
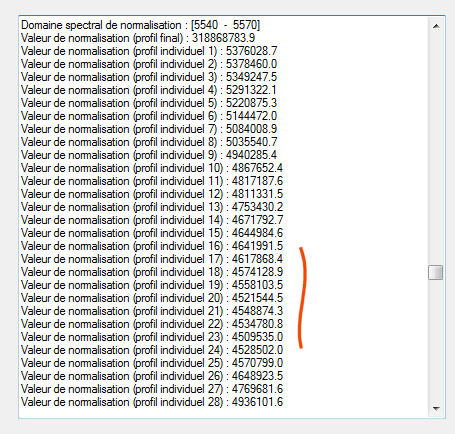
On retient un signal de 4.53 x 106 ADU au minimum de la courbe de lumière, soit 1.51 x 104 ADU/s. On calcule l'écart radiométrique en magnitude entre le signal de RR Lyrae et le signal de HD198183, soit
Dm = -2.5 log (1.51 x 104 / 4.53 x 106 ) = 3,53
Puisque la magnitude
de l'étoile HD198183 V = 4.75, on déduit immédiatement que l'éclat
de RR Lyrae dans cette même bande spectrale est V = 4.75 + Dm
= 4.75 + 3.53 = 8.28. C'est effectivement la magnitude type
de cette étoile à cet endroit de sa courbe de phase.
6. Comment convertir le signal observé dans un système photométrique
Prendre un spectre de la brillante étoile Vega. L'objet, de type A0V, est une référence photométrique primaire. En même temps, elle est très brillante (souvent trop, prendre garde à ne pas saturer le détecteur !). Voici le profil spectre avec des intensités en pas codeurs (ou comptes numériques) :
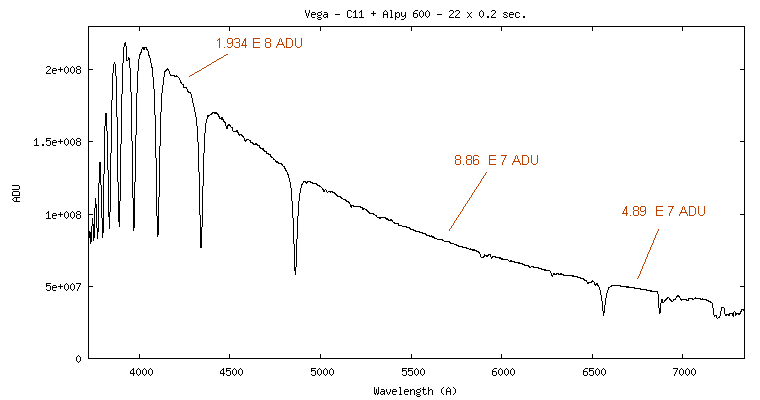
Ce spectre a été réalisé avec un télescope Celestron 9.25 et un spectrographe Alpy 600 équipé d'une fente de 18 microns. Le profil affiché est soigneusement corrigé de la réponse instrumentale + extinction atmosphérique, via une observation de l'étoile HD189183 réalisée à peu de temps d'intervalle.
Rappel : sous ISIS, pour obtenir un spectre en pas codeurs, il suffit depuis l'onglet de configuration d'entrer des valeurs nulles pour le domaine de normalisation :
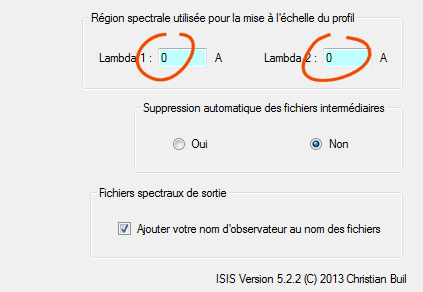
On décide de manière tout à fait arbitraire que la bande B de notre système photométrique est un filtre numérique aux fronts de raideurs infinis, entre les longueurs d'onde 4140 A et 4280 A. On moyenne le signal dans cette bande. De même, la zone de calcul du signal moyen dans la pseudo bande V est comprise entre 5450 A et 5600 A, et pour la bande R entre 6640 A et 6800 A.
Voici par exemple comment configurer ISIS pour calculer le signal dans notre bande V :
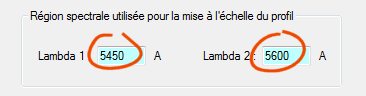
On lance le calcul du spectre, puis dans la fenêtre de sortie de résultat, on relève le signal moyen mesuré par ISIS dans la région specrale en question :

La signal en pas codeurs (ADU) est converti en magnitudes "radiométriques" grace à la formule de Pogson :
Mradiométrique = -2.5 log (Comptes numériques)
La magnitude radiométrique est directement rattachée au signal donné par l'instrument (après le prétraitement). Ce n'est pas encore la magnitude photométrique classique.
Voici la résultat trouvé lors de l'observation de l'étoile Vega (voir aussi dans le graphe du spectre de l'étoile Vega ci-avant) :
|
|
Signal en comptes numériques |
Magnitude radiométrique brute |
Magnitude radiométrique ramenée à 0 pour la bande V |
|
B |
1.93 x 108 ADU |
-20.71 |
-0.84 |
|
V |
8.89 x 107 ADU |
-19.87 |
0.00 |
|
R |
4.89 x 107 ADU |
-19.22 |
+0.65 |
Par définition, dans le système des magnitudes photométriques, les indices de couleurs (B-V) et (V-R) de l'étoile Vega sont quasi nuls. Cette étoile fixe en effet le point zéro du système des magnitudes. En réalité, le point zéro est lié à un ensemble d'étoiles, dont fait partie Vega. Malgré tout, les indices de couleurs concernés pour Vega sont inférieurs à 1/100 de magnitude. Donc pour cette étoile, nous pouvons écrire (B -V) = 0 et (V-R) = 0.
On considère par ailleurs pour Vega que V = 0 (en réalité V = 0.03, mais cela n'a aucun effet sur notre calcul). On en déduit immédiatement les équations de passage entre les magnitudes radiométriques (associées au profil corrigé de l'étoile) et les magnitudes photométriques (associées à notre propre système BVR) :
Bphotométrique
= Bradiométrique
+ 0.84
Vphotométrique
= Vradiométrique
Rphotométrique
= Rradiométrique -
0.65
C'est le jeu fondamental d'équations pour le rattachement au système photométrique BVR "propriétaire", dont on rappelle la définition dans le tableau suivant :
|
|
Longueur d'onde effective |
Bande passante |
|
B |
4210 A |
140 A |
|
V |
5525 A |
150 A |
|
R |
6720 A |
160 A |
Voici les parties du spectres de Vega isolées par ces bandes :
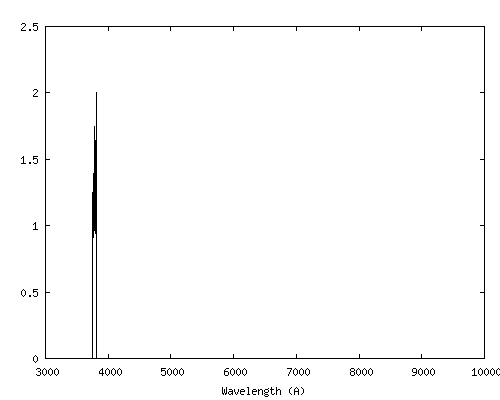
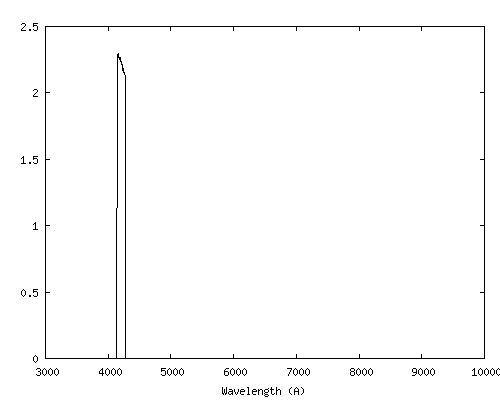
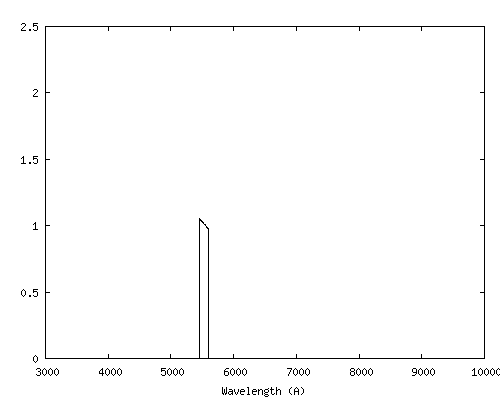
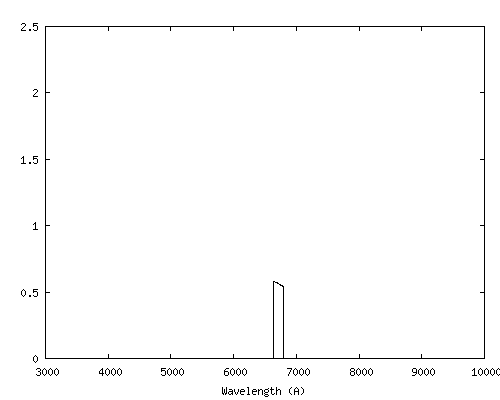
On notera que ce sont des bandes très étroites et qu'elles ont été définies pour exclure les raies de Balmer ainsi que les raies telluriques (sauf le cas de force majeure en haut à droite de cette figure, où on trouve une pseudo bande U, définie par le domaine spectral 3750 A - 3815 A).
Par comparaison, les bandes UBVR du système de Bessel sont considérablement plus larges. Voici le spectre de Vega au travers de ce système photométrique, très couramment utilisé en astronomie (voir M. S. Bessel, PASP, 102, 1181-1199, October 1990) :
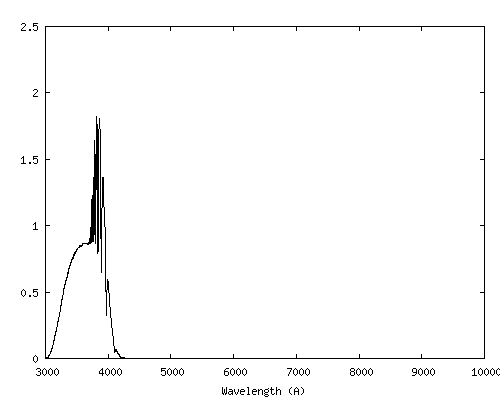
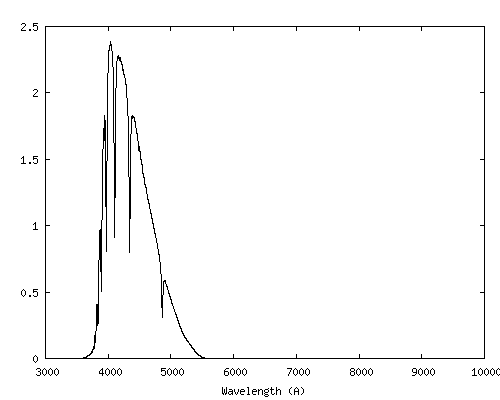
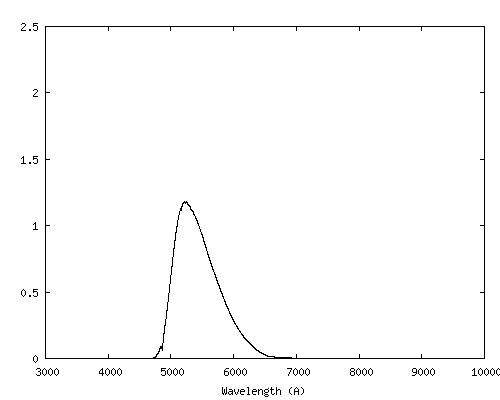
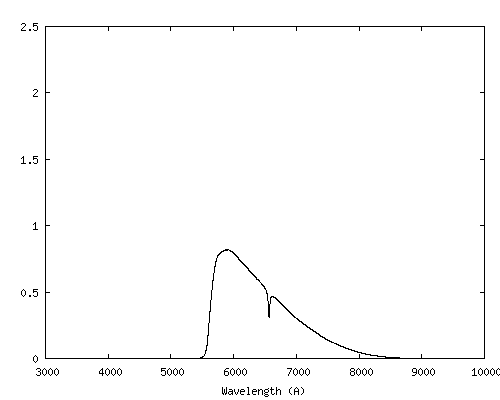
On remarque à quel point le système photométrique standard UBVR gomme une large partie de l'information spectrale. En comparaison, la spectrophotométrie offre un choix bien plus souple et riche.
A titre illustratif, le graphe suivant montre la montée en brillance de l'étoile RR Lyre dans la nuit du 7 au 8 juillet 2013. L'observation est réalisée avec Alpy 600 équipé de la fente duale 18/180. On a utilisé ici la fente de 180 microns pour une qualité photométrique maximale. Le télescope est un Celestron 9.25 exporté au foyer direct F/11. Le temps de pose est de 300 secondes dans les deux premiers tiers de l'observation, puis de 150 secondes. Bien noter que l'échelle des magnitudes est radiométrique, donc la traduction directe des comptes numériques, dans rattachement photométrique :
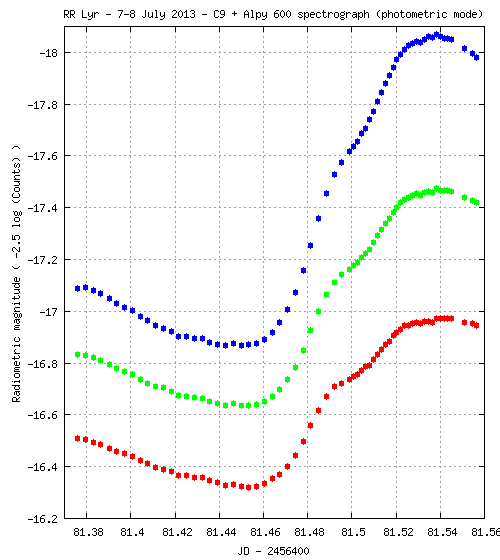
Pour la transformation en magnitude photométrique, j'utilise les équations suivantes :
Bphotométrique
= Bradiométrique
+ 0.84 + C
Vphotométrique
= Vradiométrique +
C
Rphotométrique
= Rradiométrique -
0.65 + C
avec C, la constante des magnitudes à ajouter aux magnitudes radiométriques pour trouver des magntudes photométriques. Au minimum de brillance, la magnitude radiiométrique dans la bande V est d'environ -16.6 (voir le graphe ci-dessus). Par ailleurs depuis la section 5 de cette page on sait que la magnitude V photométrique de RR Lyrae à ce momet précis de se courbe de phase est 8 environ. La constante des magnitudes est donc = C = -(-16.6 - 8) = 24.6. Voici le résultat après le rattachement à un système photométrique relativement voisin du classique BVR cher aux photométristes :
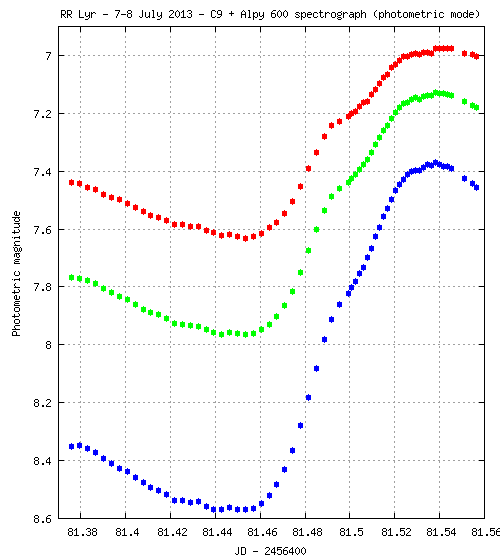
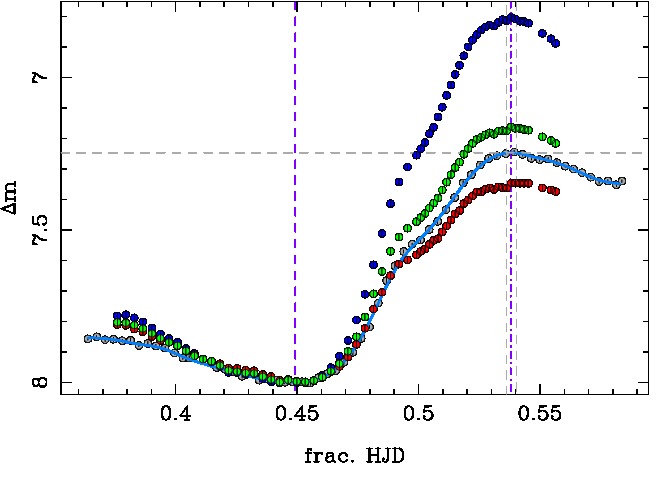
Dans le graphe ci-après,
une analyse des données spectrophotométriques RR Lyrae pour la nuit
du 7 juillet 2013, par Jean-François Leborgne (IRAP - Observatoire Midi-Pyrénées).
En bleu clair une courbe photométrique réalisée par J. F. Lebrorgne
la même nuit avec le système VTT (photométrie différentielle classique
avec un téléobjectif de 135 mm et un CCD KAF402ME sans filtre -
caméra Audine). L'accord est bon et le niveau de bruit fort équivalent
:
.
La courbe ci-après montre l'évolution de l'indice de couleur (B-V) en fonction du temps :
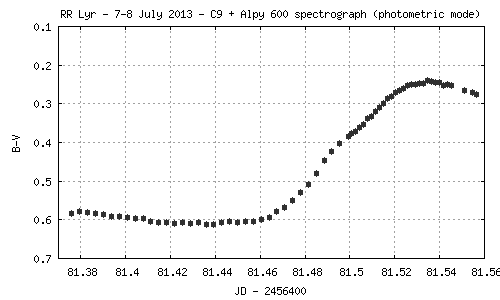
Le résultat est très faiblement
bruité alors que pourtant, les bandes spectrales de mesure sont
très étroites comparativement aux filtres BVR généralement utilisés
(voir Bessel). Une des explications est que l'acquisition de toutes
les bandes est absolument simultanée. C'est l'un des nombreux intérêts
de la spectrophotométrie.
7. Comment trouver la température photosphérique d'une étoile
On extrait des données spectrophotométriques l'intensité du signal spectral à deux longueurs d'ondes différentes dans le continuum stellaire. En considérant que l'étoile émet comme un corps noir, il est possible à partir de ces simples informations de déduire la température photosphérique de l'astre. Voici comment est établie la formule de calcul de la température (méthode des deux couleurs).


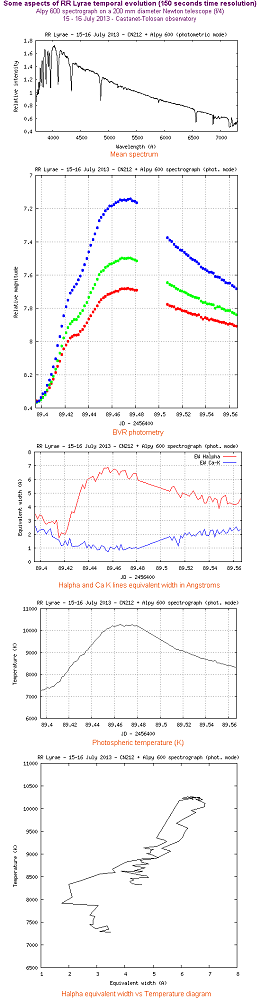
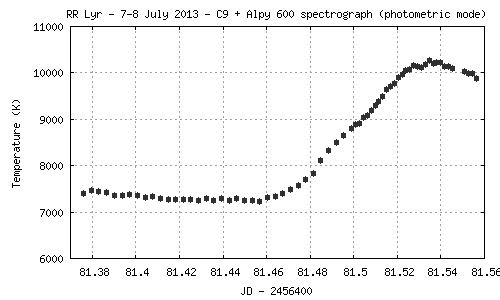
Exemple de mesure de température sur l'étoile RR Lyrae en utilisant des points de mesure dans le continuum à 4160 A et à 5525 A de longueur d'onde. La variation observée est de l'ordre de 3000 K en une heure environ :
En forme de synthèse, le poster ci-après (cliquez dessus pour l'agrandir) montre une étude de l'étoile RR Lyrae qui allie à la fois les techniques de la spectrométrie et de la spectrophotométrie sur des données observationnelles acquises avec un modeste télescope de 200 mm de diamètre et un spectrographe Alpy 600. Toute l'information vient d'un unique ensemble de spectres réalisés avec un intervalle de temps de 150 secondes avec une fente large (180 microns). Le petit diamètre et la courte focale du télescope (800 mm) sont ici des avantages : les étoiles sont très fines au foyer, et donc, malgré l'usage d'une fente large les spectres demeurent suffisamment résolus pour pouvoir mesurer avec une précision raisonnable la largeur équivalente des raies principales. La précision du système de guidage joue aussi ici un rôle essentiel (maintien de l'étoile en un point fixe de la fente) :
Le dernier diagramme montre l'évolution de la largeur équivalente de la raie Halpha en fonction la température. La relation est normalement approximativement linéaire, sauf que le phénomène d'onde de choc à JD = 2456489.415 perturbe cette harmonie, ce que ce diagramme met particulièrement bien en évidence.
On voit au travers de ces exemples que l'accès à l'observation astrophysique peut être une réalité alors qu'on ne dispose que de moyens relativement modestes (le spectrographe Alpy 600 est notamment une opportunité dans ce contexte, compte tenu de son très bon rapport qualité/prix). L’application des méthodes décrites, appliquées avec un peu de soin et de rigueur, est l’occasion d'apprendre à mesurer des phénomènes naturels spectaculaires et à s'initier à la démarche scientifique, que l'on soit étudiants ou simplement une personne nourrit par la curiosité et par l’envie de découvertes.
8. Comment convertir l'intensité des spectres en flux absolu par la pratique
Cette page en lien décrit des méthodes pratiques pour traduire l'intensité des spectres en erg/cm2/s/A. C'est une des bases de l'exploitation astrophysique des spectres. L'application numérique s'appuie sur une observation de la nova Delphini 2013 à partir du spectrographe Alpy 600. On montre aussi dans cette page comment évaluer précisément la magnitude des objets dans un système photométrique.
Annexe : standards spectrophotométriques
Une sélection de standards spectrophotométriques fondamentaux
Voir : http://www.stsci.edu/hst/observatory/cdbs/calspec.html
(extrait de la base CALSPEC)
Ces standards sont utilisés pour
étalonner les données du Hubble Space Telescope,
mais aussi celles
de bien d'autres missions spatiales et futures, ainsi que des obervations
spectrales réalisées par des observatoires sol (ESO, ...).
Vous
pouvez télécharger ces spectres en cliquant sur les liens. Par rapport
aux données originales, les spectres (au format FITS) ont été
linéarisés
en longueur d'onde, ce qui n'est pas le cas dans la base initale
STSCI. Ils sont donc immédiatement utilisables
dans des
logiciels tels que ISIS, Vspec, ... Les intensités sont en ergs/cm2/s/A.
|
03h48m50s |
-00°58'30" |
14.06 |
DA2 |
|
|
04h12m44s |
+11°51'50" |
13.88 |
DA3 |
|
|
05h05m31s |
+52°49'54" |
11.78 |
DA1 |
|
|
05h52m28s |
+15°53'17" |
13.03 |
DA1 |
|
|
08h10m50s |
+74°57'57" |
9.55 |
O5p |
|
|
09h21m19s |
+81°43'29" |
11.94 |
sdO |
|
|
10h00m48s |
-07°33'31" |
13.56 |
sDB |
|
|
10h48m24s |
+37°34'13" |
6.99 |
O9Vp |
|
|
10h39m37s |
+43°06'10" |
11.18 |
DO |
|
|
12h37m24s |
+25°04'00" |
10.51 |
sDO |
|
|
12h41m52s |
+17°31'20" |
11.82 |
sD0 |
|
|
12h57m03s |
+22°01'56" |
13.35 |
DA1 |
|
|
13h23m35s |
+36°08'00" |
11.67 |
sdO |
|
|
13h38m52s |
+70°17'08" |
12.77 |
DA3 |
|
|
15h52m00s |
+32°56'55 |
10.83 |
B2IV |
|
|
17h32m52s |
+71°04'43" |
12.53 |
A4V |
|
|
17h40m35s |
+65°27'15" |
12.48 |
A6V |
|
|
17h43m04s |
+66°55'01" |
13.52 |
A8III |
|
|
18h02m27s |
+60°43'35" |
11.98 |
A2V |
|
|
18h05m29s |
+64°27'57" |
12.28 |
A4V |
|
|
18h12m10s |
+63°29'42" |
11.74 |
A5V |
|
|
18h36m56s |
+38°47'01" |
0.03 |
A0V |
|
|
21h51m11s |
+28°51'52" |
10.51 |
Op |
|
|
21h52m26s |
+02°23'24" |
12.74 |
DA3 |
|
|
21h59m42s |
+26°25'58" |
9.68 |
O |
|
|
22h03m11s |
+18°53'03" |
7.65 |
G0V |
|
|
22h11m31s |
+18°05'34" |
9.47 |
sfF8 |
|
|
23h19m59s |
-05°09'56" |
11.83 |
D0p |